正文

由于实际要传输的信号(基带信号)所占据的频带通常是低频开始的,而实际通信信道往往都是带通的,要在这种情况下进行通信,就必须对包含信息的信号进行调制,实现基带信号频谱的搬移,以适合实际信道的传输。即用基带信号对载波信号的某些参量进行控制,使载波的这些参量随基带信号的变化而变化。因为正弦信号的特殊优点(如:形式简单,便于产生和接受等),在大多数数字通信系统中,我们都选用正弦信号作为载波。显然,我们可以利用正弦信号的幅度,频率,相位来携带原始数字基带信号,相对应的分别称为调幅,调频,调相三种基本形式。当然,我们也可以利用其中二种方式的结合来实现数字信号的传输,如调幅
-
调相等,从而达到某些更加好的特性。
一.星座图基本原理
一般而言,一个已调信号可以表示为:
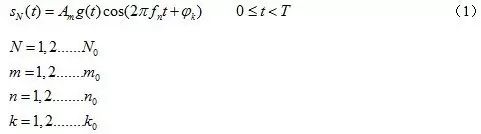
上式中,
g(t)
是低通脉冲波形,此处,我们为简单处理,假设
g(t)
=1,
0
≤T
,即
g(t)
是矩形波,以下也做同样处理。假设一共有
N
0
(一般
N
0
总是
2
的整数次幂,为
2
,
4
,
16
,
32
等等)个消息序列,我们可以把这
N
0
个消息序列分别映射到载波的幅度
A
m
,频率
f
n
和相位
φ
k
上,显然,必须有
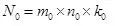
才能实现
N
0
这
个信号的传输。当然,我们也不可能同时使用载波信号的幅度、频率和相位三者来同时携带调制信号,这样的话,接收端的解调过程将是非常复杂的。其中最简单的三种方式是:
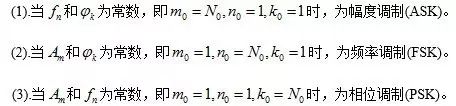
我们也可以采取两者的结合来传输调制信号,一般采用的是
幅度和相位
结合的方式,其中使用较为广泛的一项技术是正交幅度调制
(MQAM)
。
我们把(
1
)式展开,可得:
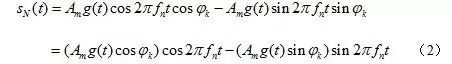
根据空间理论,我们可以选择以下的一组基向量:

来表示。当在二维坐标上将上面的向量端点画出来时,我们称之为星座图,又叫矢量图。也就是说,星座图不是本来就有的,只是我们这样表示出来的。星座图对于判断调制方式的误码率等有很直观的效用。
由此我们也可以看出,由于频率调制时,其频率分量始终随着基带信号的变化而变化,故而其基向量也是不停地变化,而且,此时在信号空间中的分量也为一个确定的量。所以,对于频率调制,我们一般都不讨论其星座图的。
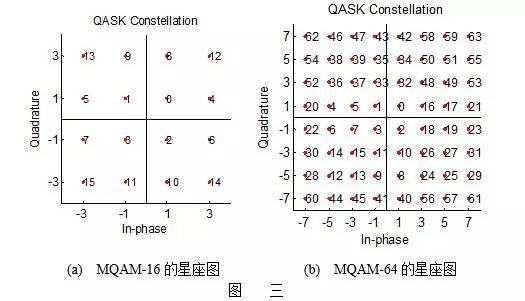
二.星座图的几个例子
下面我们就除频率调制之外的其他几种调制方式分别说明。
1
.
MASK
调制
MASK
调制是多进制幅度调制,故其载波频率
f
c
和相位
φ
(一般
取
φ
=0)为一常数,于是,其已调信号可以写成:
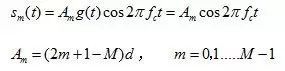
2d
是两相邻信号幅度之间的差值,此时,每个已调信号的波形可携带
log
2
M
比特的信息。
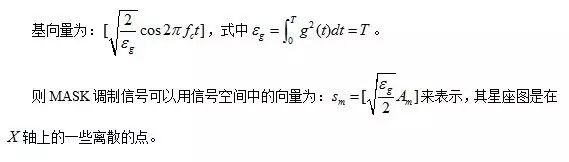

在
Matlab
中自带了画星座图的函数,上面的图调用了
modmap('ask',8)
。
2
.
MPSK
调制
MPSK
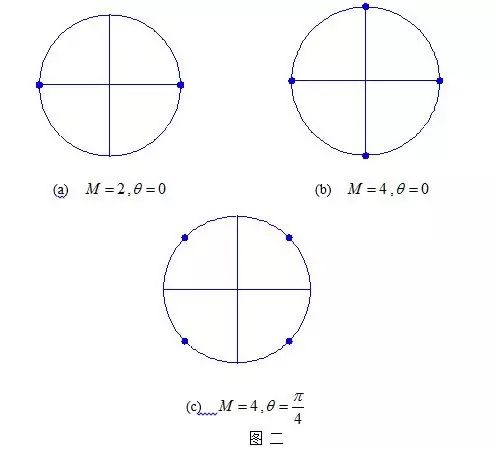
是多进制相位调制,是利用载波的多种不同相位来表征数字信息的调制方式。分为绝对相位调制和相对相位调制,此处,我们仅对绝对相位调制进行讨论。对于一个
M
相相位调制,其已调信号可以表示为:


3
.正交幅度调制
(MQAM)
一个
MQAM
信号可以看成是在两个正交载波上进行幅度调制的叠加:
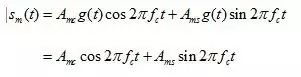
其中
g(t)
是低通脉冲波形,此处我们仍然假设为矩形波。
f
c
是载波频率,
A
mc
,A
ms
是一组幅值,
m=0,1...M-1
,这样可以将不同的信号序列映射到不同的幅值电平上。
选择基向量:
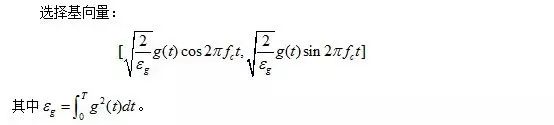
则
MQAM
信号在空间中可以表示为:

三.星座图的作用
下面简要说明一下星座图在实际情况中的应用。前面已经说了,星座图对于判断调制方式的误码率等有很直观的效用。下面我们利用
Matlab
对于
QPSK(M=4)
调制举一个例子来说明:分别选取信噪比为
0dB, 10dB, 20dB
,在接收端观察接收到的信号向量。
程序:
Fd=1;%
消息序列的采样速率
Fs=3;%
已调信号的采样速率
M=4;
for SNR_dB=0:10:20
Eb_N0=10^(SNR_dB/10);
sgma=sqrt(1/(8*Eb_N0));
x=randint(10,1,M);%
产生
0,1,2,3
等概分布的
10
个序列作为消息序列
y=dmodce(x,Fd,Fs,'psk',M);%
对
x
进行数字基带调制,方式为
QPSK
ynoise=y+sqrt(Fs/Fd)*sgma*(randn(length(y),1)+j*randn(length(y),1));%
模拟信道,加噪
figure(SNR_dB+1)
axis([-1.2,1.2,-1.2,1.2])
hold on
for i=0:M-1
plot(cos(2*pi*i/M),sin(2*pi*i/M),'.','MarkerSize',20)%
完美的星座图
end
plot(ynoise,'+')%
接收端实际接收到的信号的矢量图
hold off
end
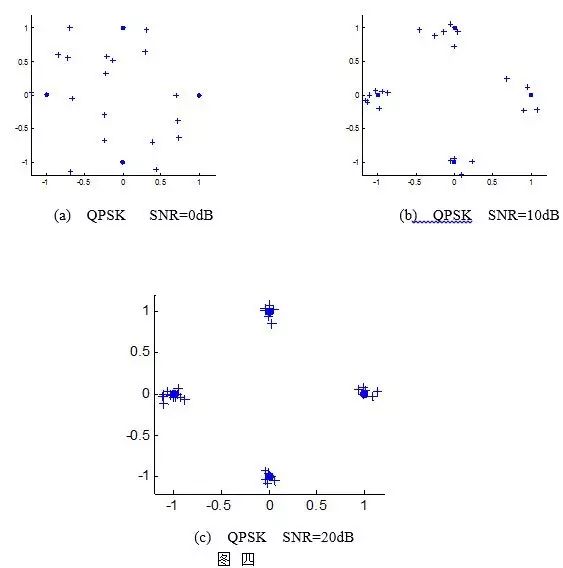
分析:
如图四所示,其中黑点是没有加入噪声时的实际情况噪声条件下的信号映射到空间中的矢量图,而加号
(+)
是在信道传输中。由此我们可以看出此时系统近似的误码率。
(a)
是信噪比是
0dB
时的情况,由于此时的噪声很大(其能量和要传输的信号一样大),在星座图上可以看出,信号受噪声影响很大,与理想情况下的矢量点偏离较远,误码率也就很高。
(b)
是信噪比是10
dB
时的情况,此时的噪声的能量是要传输信号能量的十分之一。我们可以看出,在信号空间中实际信号的分布比较集中了,误码率明显降低。
(c)
信噪比是
20
dB
时的情况,此时的噪声的能量是要传输信号能量的百分之一。我们可以看出,在信号空间中实际信号的分布非常集中了,此时的误码率已经是非常低了。
在关注微信号 eetop-1 之后
回复如下关键词
查看下列文章:
通信
:
人生
:
数学
:
-
简单说说傅立叶变换和拉普拉斯变换(z 变换)
-
傅立叶变换、拉普拉斯变换、Z变换最全攻略
-
复数的物理意义
-
傅立叶变换的物理意义
-
拉普拉斯变换的物理意义
-
卷积的物理意义
-
论频谱中负频率成分的物理意义
-
FFT结果的物理意义
-
MIT牛人解说数学体系













