矩阵在Mata中的输入和运算

往期推文 《初识MATA》 中我们介绍到，Stata中因 Mata 语言的增加，极大地简化了处理复杂数据的能力。Stata在使用矩阵时会占用大量的内存， Stata MP版本中矩阵命令最多只能处理不超过11000行/列的矩阵， 因此，很多大数据不能利用传统的Stata矩阵命令进行处理。 正如下面例子所示:

clear all

mat A=(2,6,1\3,10,12\2,9,5)

memory

mata

mata clear    //清空mata内存

A=(2,6,1\3,10,12\2,9,5)

mata memory   //查看mata内存

end

我们分别在Stata和 Mata 中输入两个相同的矩阵，结果如下：

发现 Mata 中矩阵所占用的内存远小于Stata所占用的内存。今天推文先主要给大家介绍在 Mata 中 手动输入矩阵 以及它的一些 运算 。

在 Mata 环境中，矩阵的输入以英文状态的“,”分隔各列，以“/”分隔各行。矩阵的每一个元素可以是实数、复数以及字符串。需要说明的是数字和字符串不能放在同一个矩阵中，并且字符型矩阵和数值型矩阵不能互相进行相关代数运算。

举例一：

mata

A1=(1,2,-1\3,4,-2+3i\2,5,6)

A2=(-2,1,-2\1,-2,3-1i+3i\3,6,-1)

A3=(A1,A2)   //矩阵的横向拼接

A3

A4=(A1\A2)   //矩阵的纵向拼接

A4

end

注 ：矩阵的横向拼接,要求所合并的矩阵 行数相等 ；矩阵的纵向拼接,要求所合并的矩阵 列数相等 。

限于篇幅，只展示部分结果如下：

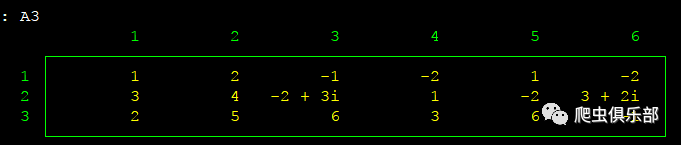
举例二：

mata

B1=("爬虫俱乐部"\"将爬虫进行到底"\"number one")

B2=("大数据分析"\"大数据挖掘"\"团队")

B3=("1"\"2"\"3")

B4=(B1,B2,B3)   //矩阵的横向拼接

B4

B5=(B1\B2\B3)   //矩阵的纵向拼接

B5

end

结果如下：

Mata 矩阵的下标分为列表下标和范围下标。对于列表下标，我们可以用诸如x[i,j]的形式来表示单个元素，x表示行，j表示列，当然i和j也可以是一个向量。同样读者也可以用范围下标来表示连续的元素，范围下标有 两种 表示方法，一种是“::”，另一种是“||”。具体用法看下面的例子：

mata

C1=A1[1,2]  //提取矩阵A1的第一行第二列的观测值

C1

C2=A1[1,.]  //提取矩阵A1的第一行的所有列的子矩阵

C2

C3=A1[.,.]  //提取矩阵A1的所有行的所有列的矩阵

C3

C4=A1[1,(1,3)]  //提取矩阵A1的第一行第一、三列的子矩阵

C4

C5=A3[1,(1::3)]  //提取矩阵A3的第一行第一、二、三列的子矩阵

C5

C6=A3[(1::2),(4::6)]  //提取矩阵A3的第一、二行,第四、五、六列的子矩阵

C6

C7=A3[|1,4 \ 2,6|]  //提取矩阵A3的第一行第四列到第二行第六列的子矩阵

C7

end

限于篇幅，此处展示部分结果如下：

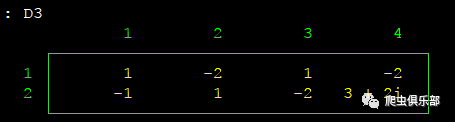
1、 转置运算符

mata

D1=A1'   //矩阵A1的转置

D2=C3'A1   //矩阵C3的转置与矩阵A1的乘积

D2

D3=(C4',C6)  //横向拼接

D3

D4=(C5',C6')

D4

end

部分结果如下：

2、 代数运算符

常见的 矩阵代数运算 有矩阵加减、矩阵相乘、数乘（矩阵乘以常数）以及矩阵A除以常数K 。

mata

E1=A1+A2   //矩阵相加

E1

E2=A1*A2   //矩阵相乘

E2

E3=A1*12   //数乘

E3

E4=A2/2   //矩阵除以常数

E4

E5=A1'+A2'   //矩阵转置相加

E5

end

注 ：与矩阵的正常计算一样，在 Mata 中两个具有 相同结构 的矩阵才能进行加减运算；第一个矩阵的行等于第二个矩阵的列相等才能进行两个矩阵间的乘除运算。

部分结果如下：

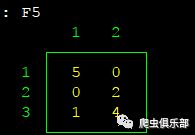
3、 冒号运算符

当使用冒号(“:”)的时候，包括加 (“+”)、减 (“-”)、乘 (“*”)、除(“/”)在内的代数运算符可以被用于元素对元素的运算。这些运算符可以用在结构相同的矩阵，也可以用于不同结构的矩阵， 需要注意的是这里的不同结构指的是满足同行数或同列数的向量才可进行运算 。举例如下：

mata

F1= (5, 0 \ 0, 2 \ 3, 8)

F2= (1, 3 \ 5, 1 \ 3, 2)

F3=F1:*F2   //矩阵元素相乘

F3

F4=F1:+F2   //矩阵元素相加

F4

F5=F1:/F2   //矩阵元素相除

F5

F6=F1:-F2  //矩阵元素相减

F6

end

部分结果如下所示：

4、 逻辑与关系运算符

mata

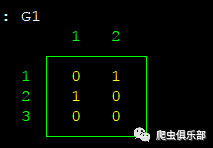
G1=(!F1)  //矩阵F1中的元素是否非零

G1

G2=(F1==F2')  //判断矩阵F1 所有元素是否和F2转置矩阵的所有元素相等

G2

G3=(F1!=F2' )  //判断矩阵F1是否与F2的转置矩阵有不相等的元素

G3

G4=(F1>=F2)  //判断矩阵F1 的所有元素是否大于等于矩阵F2的所有元素

G4

G5=(F1[2,1]=0 )  //判断矩阵F1的第二行第一列元素是否为0

G5

end

结果如下：

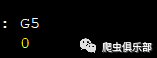
注 ：

(1) 逻辑运算符“!”可以用于标量、向量和矩阵，并在各元素相应的位置上返回0或1，其它的逻辑运算符(“&”，“|”)只能用于标量。

(2) 关系运算符“!=”可以用于不同结构的向量和矩阵，其它的关系运算符(“>”，“>=”，“

如下所示：

可以看到，因为矩阵F1和矩阵F2转置的结构不同，所以Stata报错。

以上都是在 Mata 环境中手动输入矩阵及其简单运算，如果我们想要修改矩阵的行列名称、生成矩阵的逆矩阵以及生成一些特殊矩阵等，就需要用到一些 Mata 函数 ，在后面的推文我们会继续介绍哟。

看不懂的记得戳下方视频哦~

注：此推文中的图片及封面（除操作部分的）均来源于网络！如有雷同纯属巧合！