使用Gluon实现的一个简单的线性回归模型

引言：本文介绍的主要内容为如何使用Gluon实现一个简单的线形回归模型，旨在了解模型建立与训练的一般过程。

（1）线性回归

给定一个数据点集合 X 和对应的目标值 y ，线性模型的目标是找一根线，其由向量 w 和位移 b 组成，来最好地近似每个样本 X[i] 和 y[i] 。用数学符号来表示就是我们将学 w 和 b 来预测

y ^ = X w + b

并最小化所有数据点上的平方误差

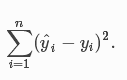
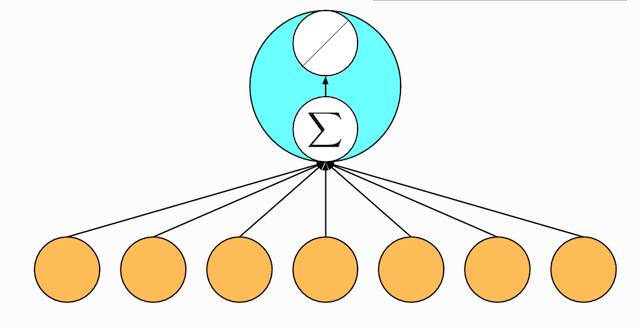
你可能会对我们把古老的线性回归作为深度学习的一个样例表示很奇怪。实际上线性模型是最简单但也可能是最有用的神经网络。一个神经网络就是一个由节点（神经元）和有向边组成的集合。我们一般把一些节点组成层，每一层使用下一层的节点作为输入，并输出给上面层使用。为了计算一个节点值，我们将输入节点值做加权和，然后再加上一个激活函数。对于线性回归而言，它是一个两层神经网络，其中第一层是（下图橙色点）输入，每个节点对应输入数据点的一个维度，第二层是单输出节点（下图绿色点）。

f ( x ) = x ）作为激活函数。

（2）创建数据集

这里我们使用一个人工数据集来把事情弄简单些，因为这样我们将知道真实的模型是什么样的。具体来说我们使用如下方法来生成数据

y[i] = 2 * X[i][0] - 3.4 * X[i][1] + 4.2 + noise

这里噪音服从均值0和标准差为0.01的正态分布

In [1]:

from mxnet import ndarray as nd
from mxnet import autograd
from mxnet import gluon
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
X = nd.random_normal(shape=(num_examples, num_inputs))
y = true_w[0] * X[:, 0] + true_w[1] * X[:, 1] + true_b
y += .01 * nd.random_normal(shape=y.shape)

注意到X的每一行是一个长度为2的向量，而y的每一行是一个长度为1的向量（标量）。

（3）数据读取

当我们开始训练神经网络的时候，我们需要不断读取数据块。 这里使用 data 模块来读取数据。

In [2]:

batch_size = 10
dataset = gluon.data.ArrayDataset(X, y)
data_iter = gluon.data.DataLoader(dataset, batch_size, shuffle=True)

In [3]:

for data, label in data_iter:
    print(data, label)
    break

[[ 0.4054271   0.85561502]
 [ 0.46009848 -0.20287366]
 [-0.033391    0.72138798]
 [-0.17717248 -1.17355824]
 [ 1.52278841 -0.47990882]
 [ 1.20405591  1.31119514]
 [ 1.35970342  0.79950231]
 [ 0.86404645 -1.40260971]
 [ 1.48596764 -1.61362338]
 [-1.4760977  -0.18857454]]

[  2.0888629    5.80537605   1.67896223   7.84740686   8.88370323
   2.14853954   4.20148134  10.71073437  12.63388157   1.88829148]

（4）定义模型

当我们手写模型的时候，我们需要先声明模型参数，然后再使用它们来构建模型。但 gluon 提供大量提前定制好的层，使得我们只需要主要关注使用哪些层来构建模型。例如线性模型就是使用对应的 Dense 层。

虽然我们之后会介绍如何构造任意结构的神经网络，构建模型最简单的办法是利用 Sequential 来所有层串起来。首先我们定义一个空的模型：

In [4]:

net = gluon.nn.Sequential()

然后我们加入一个 Dense 层，它唯一必须要定义的参数就是输出节点的个数，在线性模型里面是1.

In [5]:

net.add(gluon.nn.Dense(1))

（注意这里我们并没有定义说这个层的输入节点是多少，这个在之后真正给数据的时候系统会自动赋值。）

（5）初始化模型参数

在使用前 net 我们必须要初始化模型权重，这里我们使用默认随机初始化方法（之后我们会介绍更多的初始化方法）。

In [6]:

net.initialize()

（6）损失函数

gluon 提供了平方误差函数：

In [7]:

square_loss = gluon.loss.L2Loss()

（7）优化

同样我们无需手动实现随机梯度下降，我们可以用创建一个 Trainer 的实例，并且将模型参数传递给它就行。

In [8]:

trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': 0.1})