专栏名称: 开智部落

「开智部落」是基于认知学徒制设计的学习共同体。

21 世纪的科学：复杂性科学入门指南

开智部落 · 公众号 · · 2017-09-15 23:38

正文

— Note170915001 —

让我们来开启一场思维范式升级之旅吧 ▼

复杂性科学（Science of Complexity）是一门新兴的边缘、交叉学科，被研究者誉为科学史上“继相对论和量子力学之后的又一次革命”、“21世纪的科学”。凯文·凯利也曾提出：“如果说原子是20世纪科学的图标，那么在21世纪，原子成为过去，取代它的是充满活力的网络。”

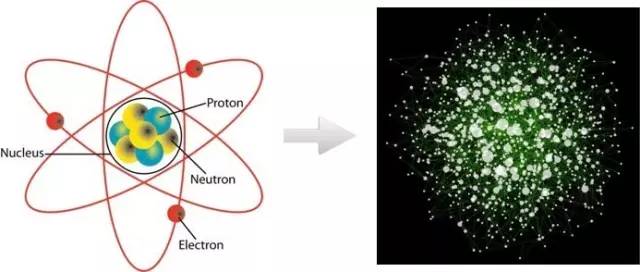
为什么要学习它？

我们一般认为，学习一门新的科学，获得的将是新的解决问题的方法和新的技术框架，但实际上，我们获得的经常是一种看待问题的新角度和全新的世界观。

复杂性科学就是这样一门新的科学，它在20世纪末兴起，横跨相当多科学的学科，虽然现在还属于迅速发展阶段，但已经大大扩展了人类认知边界，使得我们对世界的认识从简单还原论到复杂整体论、从关注事物本身到网络思维、从线性到非线性、从均衡到非均衡。所以学习复杂性科学是让我们用新思维范式替代旧思维范式的旅程。

复杂性科学简介

研究背景

17世纪以来，还原论就一直在科学中占据着主导地位。

所谓还原论，就是去追根究底，对事物进行拆解，追问它们是由什么组成的。比如人可以还原为水、蛋白质、脂类、糖类和无机盐以及维生素，往下层层分解，还能分解成原子、电子、质子、夸克……人就是由这些基本物质构成。

花了三百年时间拆解后，科学家们终于开始把这个程序颠倒过来。他们开始研究这些东西如何融合在一起，形成一个复杂的整体。

比如生物学家们揭示脱氧核糖核酸的分子机制后，开始探索：上千万亿这样的分子是怎样使自己组合成有生命的物体？

类似的还有，脑科学领域开始研究“智能”和“意识”是如何由几十亿个神经细胞的联结中涌现出来？

物理学也有许多深奥的谜题需要解开：为什么简单的粒子会自动组成雪花、飓风、星球这样复杂的结构？为什么受简单规律支配的粒子会产生令人震惊、无法预测的行为？

经济学家也开始发现新古典经济学中视而不见的问题：经济系统中自利的个体如何形成结构复杂的全球市场？为什么高科技公司都蜂拥到硅谷安营扎寨？

一些学者强烈地感觉到，这些在不同学科中发生的问题具有深刻的相似性。而还原论无法解释这个现象：简单个体的大规模组合后，会形成复杂行为，即“整体大于部分之和”。

这些学者还发现另外一些无法解释的现象。

热力学第二定律告诉我们，系统会自发地朝着最大熵状态演化。根据这条定律，如果任凭事物自由发展，铁会生锈、水会变凉、树会腐烂，房间不会自己变干净，饮料如果泼到地上，永远也不会回到杯子里。自然界对解体结构，要比建立结构和秩序更感兴趣。

可是倒下的树虽然会腐烂，同时又有新的树木不断生长起来，种子和胚胎能够称之为完全成熟的或生物。与通常情形中的有序消退无序（熵）增长相反，宇宙却在永不停歇地从无序中产生有序。

于是他们开始询问，宇宙为什么会永不歇息地形成秩序和结构？系统为何能从随机无物开始，自主发展成复杂的整体？为什么那么久了宇宙都没有解体？这种逆熵的自组织系统是如何成为可能？

复杂性研究就诞生于这群谜团之中。

研究对象

复杂性科学的研究对象是复杂系统。目前对于复杂系统有一个比较通俗的定义：由大量相互作用的成分组成，不存在中央控制，通过简单运作的规则会产生出复杂的集体行为和复杂的信息处理，并通过学习和进化产生适应性。包括大脑、免疫系统、细胞、昆虫社会、全球经济、生物进化、万维网等等。

我们还可以把复杂系统简单地理解为介于秩序和混沌之间的系统。它既不像闹钟、集成电路板这类有序的系统，也和飓风、湍流那种无法预测的混沌系统相去甚远。想象你正在用手机玩一个控制小球的游戏，小球受随机力的驱动，会在跷跷板上滚动，你需要倾斜手机，避免小球掉落。如果小球即将或者已经朝着左侧运动，你要向右倾斜手机，尽量让它保持在跷跷板中间。这种没有完全固定在某个位置，但也没有滚落跷跷板的持久不均衡的状态，就是复杂系统所在之处。这个地方——经常被称为混沌的边缘——就是系统中各种因素没有静止在某一个状态，但也没有动荡至解体的那个地方；就是生命有足够的稳定性来支撑自己的存在，又有足够的创造性使自己名副其实为生命的那个地方。

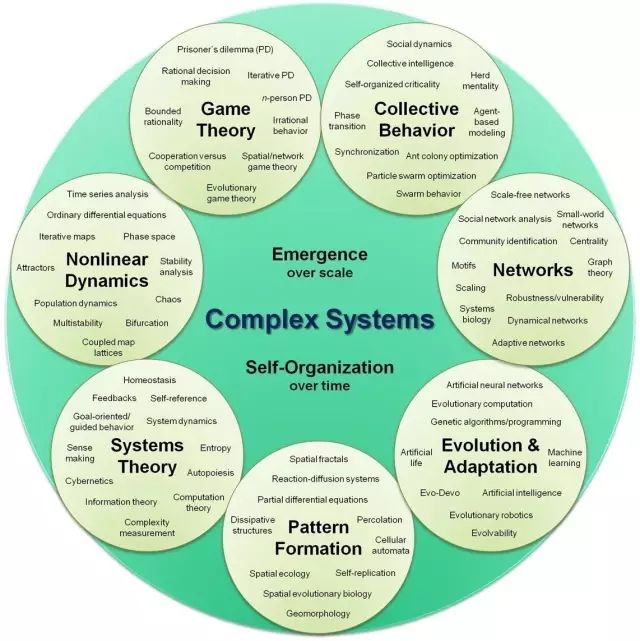
因为复杂系统不存在中央控制者，我们将它成为自组织（self-organizing），因为简单规则以难以预测的方式产生出复杂行为，我们有时也称之为涌现（emergent）。下图出自维基“复杂系统”词条，图中对复杂系统的定义是：随着时间演化，出现自组织，在不同的尺度上，出现涌现。

从图中，我们还可以看到复杂系统涉及许多研究领域，包括：系统理论、非线性动力学、博弈论、集体行为、复杂网络、演化和适应性、斑图形成等等。

核心问题

复杂性科学研究的核心问题是：

涌现和自组织行为是如何产生的？

对应到自然和社会中的问题是：

细胞如何自组织成眼睛和大脑？
经济系统中自利的个体如何形成结构复杂的全球市场？
所谓的“智能”和“意识”是如何从不具有智能和意识的物质中涌现出来的？
我们能不能建造出真正具有生命和智能的机器？
……

复杂性科学核心概念

1. 自组织临界性

宇宙为何能以大爆炸中产生的几种粒子开始，变得越来越复杂，最终演变成现在这个丰富多彩的世界呢？为什么宇宙这么久了还没解体？这背后是否有“上帝之手”在干预？如果没有，是偶然还是必然？

Per Bak给出了答案。他指出“自组织临界性（Self-Organized Criticality，SOC）是自然界趋向最大复杂性的驱动力”，“是目前所知的产生复杂性的唯一普遍机制”，它可以解释诸如生物进化和物种灭绝、地震、交通阻塞等种种现象。

SOC指的是复杂系统能够通过一个漫长的自组织过程演化到一个临界态，处于临界态的一个微小的局域扰动可能会通过类似“多米诺效应”的机制被放大，其效应可能会延伸到整个系统，形成一个大的雪崩（灾变）。处于临界态的系统中会出现各种大小的“雪崩”事件，并且雪崩的时间尺度和空间尺度均服从幂律分布，幂律分布是自组织临界态的指纹。分形现象和1/f噪声是自组织临界现象的空间和时间的印记（Bak）。

所谓“自组织”是指该状态的形成主要是由系统内部组织间的相互作用产生，而不是由任何外界因素控制或主导所致。所谓“临界态”是指系统处于一种特殊敏感状态，微小的局部变化可以不断放大、扩延至整个系统。

沙堆模型

Bak 等人使用沙堆模型来形象地说明自组织临界性的形成和特点。

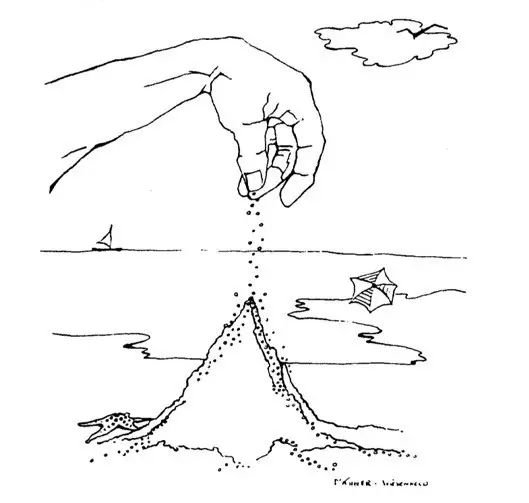
他们让沙子一粒一粒落在桌上，形成逐渐增高的一小堆，借助慢速录象和计算机模仿，精确地计算每在沙堆顶部落置一粒沙会连带多少沙粒移动；初始阶段，落下的沙粒对沙堆整体影响很小；然而当沙堆增高到一定程度，落下一粒沙却可能导致整个沙堆发生坍塌。Bak等人由此提出“自组织临界”的理论；沙堆一达到“临界”状态，每粒沙与其他沙粒就处于“一体性”接触，那时每粒新落下的沙都会产生一种 “力波”，尽管微细，却能贯穿沙堆整体，把碰撞次第传给所有沙粒，导致沙堆发生整体性的连锁改变或重新组合；沙堆的结构将随每粒新沙落下而变得脆弱，最终发生结构性失衡——坍塌。临界态时，沙崩规模的大小与其出现的频率呈幂函数关系。

鸟群迁徙

我们还可以借助鸟群迁徙来帮助我们更好地理解自组织临界性。

在天空中飞翔的鸟群，常常需要躲避各个方向的捕食者。一旦有危险，它们会快速做出反应，不断切换自己的阵型，向前、转弯、变形……我们不禁会为这种鸟群的自组织感到惊讶，整个鸟群看起来就像一个巨型的“生物体”，很难相信这种转变是由许许多多独立的、无智慧的个体聚在一起完成的。

这种现象暗示了鸟群被集中在某个临界性上。计算机科学家们总结了群体运动模拟的几个核心要点：

体积排斥：每个模拟的个体（boid）都会占据一定的体积，而这些体积永远不会相交，即每个个体都会避免与最近的个体发生碰撞。
速度对齐：每个个体与其近邻的个体们保持速度同步。
聚集倾向：粒子不会倾向于独立行动（粒子群保持维持），每个个体会尽量与附近个体靠近，避免被孤立。

从这三个基本原则出发，就可以对动物的群体运动进行非常逼真的模拟。有趣的是，这三条规则都是局部的规则，并没有“领导”在其中发挥作用，任意的个体都仅仅只是根据自己附近的其它粒子的运动情况调整自己的运动方向，就可以产生如此复杂“智能”的行为。

2. 复杂适应系统和涌现

复杂适应系统统（Complex Adaptive System，CAS）是一类具有代表性的复杂系统。它的基本思想是：CAS的复杂性起源于其中主体（Active Agent）的适应性，正是这些主体与其它主体以及环境间的相互作用，不断改变着它们的自身，同时也改变着环境。CAS最重要的特征是适应性，即系统中的主体能够与环境以及其它主体进行交流，在这种交流的过程中“学习　或积累经验”，不断进行着演化学习，并且根据学到的经验改变自身的结构和行为方式。各个底层主体通过相互间的交互、交流、可以在上一层次，在整体层次上涌现出新的结构、现象和更复杂的行为。这个过程，主体与环境不断反复交流，永不停止的相互作用、相互影响、相互进化。

复杂适应系统的特性

系统具有明显的层次性，各层之间的界线分明。
层与层间相对独立，层与层之间的直接关联作用少，主体主要与同一层的主体进行交互。
主体具有智能性、适应性、主动性。系统中的主体可以自动调整自身的状态、参数以适应环境，或与其它主体进行协同、合作或竞争，争取最大的生存机会或利益，这种自发的协作和竞争正是自然界生物“适者生存，不适者淘汰”的根源。这同时也反应出复杂适应系统是一个基于主体的，不断演化发展的系统。在这个演化过程中，主体的性能参数在变，主体的功能、属性在变，整个系统的功能结构也产生了相应的变化。　
主体具有并发性。系统中的主体是并行地对环境中的各种刺激作了出应，进行演化。　
引进了随机因素的作用，使它具有更强的描述和表达能力。

主体的基本性质

复杂性系统使用适应性主体一词，是为了强调它的主动，强调它有自己的目标，内部结构和生存动力。

主体在适应和演化过程中有七个基本性质：

聚集（特性）：主体可以在一定条件下，在双方彼此接受时组成一个新的主体——聚集主体，在系统中像一个单独的主体那样行动。
标识（机制）：标识对聚集主体形成起作用，就像因特网上的一条消息标题会让会议组的成员联结起来。
非线性（特性）：主体以及它们的属性在发生变化时，并非遵从简单的线性关系。特别是在与系统的反复交互作用中，这一点更为明显。　
流（特性）：在主体与环境之间存在有物质资源、能量和信息流，这些流的渠道是否畅通，周转迅速到什么程度，都直接影响系统的演化过程。
多样性（特性）：在适应过程中由于种种原因，主体之间的差别会发展与扩大，最终形成分化。
内部模型（机制）：这一点表明了层次的观念。每个主体都有复杂的内部机制。对于整个系统来说，这就统称为内部模型。
积木（机制）：复杂系统常常是由相对简单的一些部分，通过改变组合方式而形成的。因此，复杂性往往不在于积木的多少和大小，而在于原有积木的重新组合。

3. 复杂网络

许多自然、技术和文化现象经常被描述为网络。大脑是神经元通过突触连接起来的网络；社会是由各种各样的关系连接起来的人（或组织）组成的网络；万维网是现代社会的典型网络。网络可以定义为：由边连接在一起的节点组成的集合。节点对应网络中的个体（例如神经元、人、网站），边则是节点之间的关联（例如突触、社会关系、网页超链接）。复杂网络是由数量巨大的节点和节点之间错综复杂的关系共同构成的网络结构。

随机生成的BA模型复杂网络

网络科学的目的就是提炼出这些网络的共性进行研究。同时，网络科学家也希望能理解自然界中的网络是如何发展而来的，以及它们是如何随时间变化的。

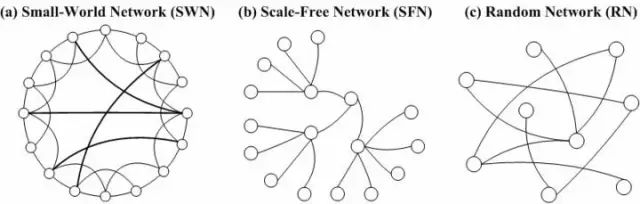
小世界网络

人们常说“这世界真小”，而几乎所有人都有过“小世界”的经历：遇到一个陌生人不久后，发现“我们居然有共同的朋友”，又或者突然有一天发现，你认为不会有交集的两个朋友原来互相认识。

这种出乎意料的关系到底有多常见？这个世界到底小到什么程度？20世纪50年代，哈佛大学的心理学家米尔格兰姆对这个问题产生了兴趣。他设计了一个实验，想弄清在美国一个人平均要通过几个熟人关系才能联系到另一个人。最后发现，一个人平均通过6个熟人就能找到想要联系的人。这个发现后来被称为“六度分隔（six degrees of separation）”。

米尔格兰姆受限于当时的技术，只做了小范围的实验。30多年后，邓肯·沃茨等人利用互联网技术在全球范围内对“六度分隔”理论进行了大规模验证。沃茨的验证得出，成功的信息链表明，志愿者将信息传送到任何一个目标“估计需要5到7个步骤，平均数正是6个步骤”。同时，他们还从数学上定义了小世界网络的概念，并且研究了怎样的网络结构会有这种特性。

先看一个最简单的规则网络（左图）：由60个节点组成的环，每个节点与相邻的两个节点相连。两个节点之间的路径长度就是两个节点之间最短路径的边的数量，平均路径长度就是网络中所有节点之间的路径长度的平均值，所以这个规则网络的平均路径长度是15。

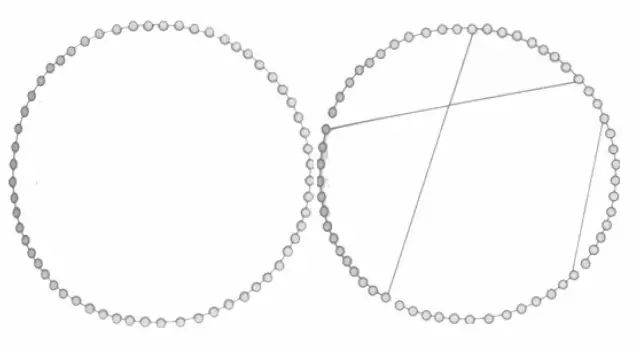
有趣的是，沃茨对这样的网络稍微改动，随意增加三条长连接，平均路径长度就降到了9。沃茨还发现，节点数越多，效应越明显。例如一个1000个节点的规则网络，平均路径是250，如果增加5%的连接，平均路径长度会一下降到20。但不管网络的规模有多大，前5个随机连接会将平均路径长度减少约一半。

所以小世界的特性是：一个网络如果只有少量的长程连接，相对于节点数量来说平均路径却很短，则为小世界网络。小世界网络也常表现出高度集群性：任选三个节点A、B、C，如果A与B、C相连，则B与C也很有可能相连。真实世界的许多网络都有小世界特性，比如我的朋友的朋友也很有可能是我的朋友。

无尺度网络

无尺度网络是一种更类似现实世界网络的小世界网络。

在万维网中，节点是网页，边是网页之间的超链接。假设网页A有个链接指向网页B，而网页B没有链接指向网页A，则A有一个出连接，B有一个入连接。我们将一个网页的入连接数称为网页的入度。大部分网页的入度很低，而极少部分网络的入度很高。

研究者发现，网页入度分布可以用非常简单的规则来表示：入度为k的网页数量正比于1/k²（k必须≥1000）。从下图可以看到，入度k为1000的网页相对较多，随着k增大，频率下降很快，到k为10000时，网页数量已经很少了。如果我们改变尺度，把k为10000的那个区域放大，就会出现第二幅图的分布情况。第三幅图可以看到更大的尺度仍然有相同的现象。这种分布满足幂率分布，被称为自相似，因为不管在哪种尺度上进行绘制，形状都一样。这就是无尺度一词的由来。无尺度网络有4个显著特征：

相对较少的节点具有很高的度（中心节点）；
节点连接度的取值范围很大（度的取值多样）；
自相似性；
小世界结构。所有的无尺度网络同时也具有小世界特性，但不是所有具有小世界特性的网络都是无尺度网络。

无尺度网络对节点的随机删除具有稳健性，但如果中心节点失效或是受到攻击就会非常脆弱。原因很简单：如果随机删除节点，则极有可能删除的是低连接度的节点，因为网络中绝大部分节点都是低连接度节点。但如果删除了中心节点，网络就有可能会失去无尺度特性，并且无法正常运转。例如，谷歌出故障会对整个万维网形成很大冲击。

4. 幂率分布

在自然界与日常生活中，包括身高、体重、考试成绩、篮球赛得分、地区降水量、各物种的数量等等都遵循正态分布。正态分布有一定的尺度——比如，身高是70~270cm，考试成绩是0~100分。在正态分布中，平均值同时也是频率最高的值，例如165cm既是平均身高也是最常见的身高。正态分布形似钟形，又经常称之为钟形曲线。

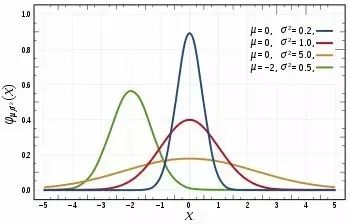
另一种常见的统计现象是幂率分布。简单地说就是两个变量为幂函数的关系。

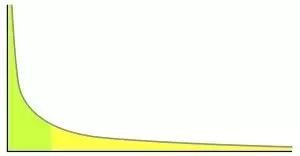
自然界与日常生活中也有许多事件规律遵循幂率分布，比如地震规模大小的分布、月球表面上月坑直径的分布、行星间碎片大小的分布、太阳耀斑强度的分布、计算机文件大小的分布、战争规模的分布、人类语言中单词频率的分布、大多数国家姓氏的分布、论文被引用的次数的分布、网页被点击次数的分布、书籍及唱片的销售册数或张数的分布、每类生物中物种数的分布、甚至电影所获得的奥斯卡奖项数的分布、个人收入的分布等等，都是典型的幂律分布。

“80/20法则”常被用于描述收入分配中出现的幂率分布，即一个国家80%的财富集中在这个国家20%的高收入人群中。但当我们用“放大镜”来看一个幂率分布的“尾巴”时，我们还会继续得到与原来的幂指数完全相同的一个幂律分布，也就是说，把那20%高收入的人选出来，再对他们进行统计，会发现这些人财产总和的80%依然会集中在这些人的20%中。

这种现象通常是因为形成了某种正反馈，在很多幂律形成中，我们都能看到类似的正反馈：大网站每天有大量的用户访问、社交网络上的大V更容易吸引新用户关注。所以幂率往往代表着某种增长法则，我们的技术、财富往往并不是线性增长，而是指数级增长。

带来的思维转变

不是科学家的人总认为科学是演绎出来的。但其实科学主要是通过比喻而来的。现在的情形是，人们头脑中的某一类比喻发生了变化。——布莱恩·阿瑟

十八世纪的隐喻认为宇宙是台简单、有规律、可预测、能够自我运行的牛顿式的机器。而复杂性理论的隐喻，似乎更接近一棵树从种子长成参天大树，或是一群头脑简单的小鸟有机自组，复杂而类似生命的行为是几条简单的、由下而上的规则所导致的结果。

正是这个隐喻的变化给我们带来一整个世界观的改变。

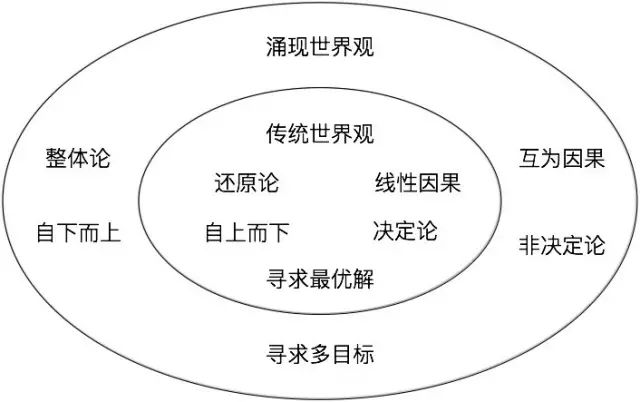
简单还原到复杂整体

传统科学强调还原论，还原论最早的倡议者之一笛卡儿这样描述他的科学方法：“将面临的所有问题尽可能地细分，细至能用最佳的方式将其解决为止”，并且“以特定的顺序引导我的思维，从最简单和最容易理解的对象开始，一步一步逐渐上升，直至最复杂的知识”。复杂性科学则复兴了整体论，认为整体不一定能还原为部分，部分之和不一定等于整体。

自上而下到自下而上

在做某件复杂的事情时——比如治理十亿人口或靠两条腿行走，人们最常想到的办法就是，按顺序列出一个需要完成的任务清单，然后在中央指挥部或大脑的指令下完成这些任务。这种“唯中央意图”遵循的是自上而下的控制思路。当年的计划经济就是按这种合乎逻辑却又极不切合实际的方式运作的。

直到现在，自上而下控制的方法仍然随处可见：我们在产品启动之时，就定好所有功能和规则，然后按步执行，而不是想办法尽快地与用户沟通想法和原型，让产品在一次次碰撞中生长；我们规划孩子的未来，而不是创造环境让他自己成长；我们“管理”团队，而不是激发团队的可能，让他们引导自己前进。

历史已经告诉我们，面对一个复杂系统，这种“自上而下控制”是效率最低的方式，更好的方法，是提供土壤，让它自下而上的自然涌现。

线性到非线性

我们的世界有些事情是线性运作的。比如声音是一个线性系统，当双簧管和弦乐器合奏时，你依然可以将它们单独地分辨出来；再比如你在街头买了一份报纸，对你去超市买一支牙膏不会有什么影响。

然而，世界中大多数事情不是线性的。我们的大脑就不是线性的：虽然双簧管和弦乐的声音独立进入你的耳朵，但是这两种乐器的和声在你情感上产生的影响远远大于这两种乐器的单独作用；数百万人做出的购买决定可能会互相影响，从而导致经济繁荣或萧条，而经济气候又会反过来影响购买力。

这是一种交叉的因果关系：A影响其它一切，而其它一切又反过来影响A。真正的起因将在网络中横向传播开来，最终触发某一特定事件的原因将无从获知。用数学来表示这个特征，就是个非线性的方程式：画出来的图线是弯曲的。

所以我们要谨慎避免用简单的线性因果思维去解释复杂现象，比如某某产品做了这个功能活跃度大大提升，所以我也增加这个功能就好了。

寻求最优解到寻求多目标

想象一局象棋，最理想的情况是，一开始两个棋手就能够在脑海中计算所有可能性，然后开始布局最佳棋步。但没有人会这么下棋，因为这个可能性是无穷无尽的。人们实际上能够预测和采取行动的内容与所谓的“最优”相去甚远。所以你要保持尽可能多的选择。你选择的是可生存的和可行的方案，而不是最优的方案。你要做的是在前途未卜的世界上变得更强健、更有生存能力。

因此，我们要做的是不断行动，让机会涌现，然后抓住它。

成功孕育成功

古语云“失败是成功之母”。它可以宽慰我们，让我们在失败时不会气馁，东山再起。但我们不能忽略的是更常见的收益递增现象。每当你使用一个想法、一种语言或者一项技能时，你都在强化它、巩固它并使其更具被重用的可能。这就是所谓的正反馈或滚雪球。成功孕育成功。任何改变其所处环境以使其产出更多的事物，玩的都是收益递增的游戏。这个定律在经济学、生物学、计算机科学以及人类心理学中都起作用。地球上的生命改变着地球以产生更多的生命。信心建立起信心。秩序造就更多的秩序。既得者得之。