专栏名称: Python学习交流

每天更新，更新python相关的知识。希望诸君有所收获！

Python最牛逼数据分析库！月薪35K大牛：整理的NumPy详细教程！

Python学习交流 · 公众号 · Python · 2018-01-30 21:54

正文

NumPy在数据分析就像Django在web开发中那样出名，就是老大哥，也是在工作中最常用的库，没有之一，今天给大家详细的讲解一下这个库的妙用！

103456743

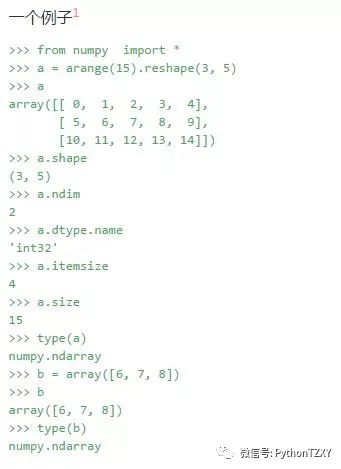
ndarray.ndim

数组轴的个数，在python的世界中，轴的个数被称作秩
ndarray.shape

数组的维度。这是一个指示数组在每个维度上大小的整数元组。例如一个n排m列的矩阵，它的shape属性将是(2,3),这个元组的长度显然是秩，即维度或者ndim属性
ndarray.size

数组元素的总个数，等于shape属性中元组元素的乘积。
ndarray.dtype

一个用来描述数组中元素类型的对象，可以通过创造或指定dtype使用标准Python类型。另外NumPy提供它自己的数据类型。
ndarray.itemsize

数组中每个元素的字节大小。例如，一个元素类型为float64的数组itemsiz属性值为8(=64/8),又如，一个元素类型为complex32的数组item属性为4(=32/8).
ndarray.data

包含实际数组元素的缓冲区，通常我们不需要使用这个属性，因为我们总是通过索引来使用数组中的元素。

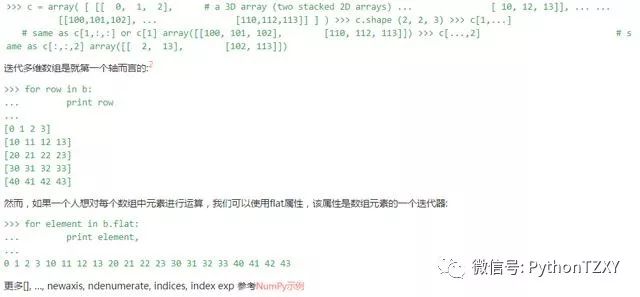
x[1,2,…] 等同于 x[1,2,:,:,:],
x[…,3] 等同于 x[:,:,:,:,3]
x[4,…,5,:] 等同 x[4,:,:,5,:].

进阶

广播法则(rule)

广播法则能使通用函数有意义地处理不具有相同形状的输入。

广播第一法则是，如果所有的输入数组维度不都相同，一个“1”将被重复地添加在维度较小的数组上直至所有的数组拥有一样的维度。

广播第二法则确定长度为1的数组沿着特殊的方向表现地好像它有沿着那个方向最大形状的大小。对数组来说，沿着那个维度的数组元素的值理应相同。

应用广播法则之后，所有数组的大小必须匹配。更多细节可以从这个文档找到。

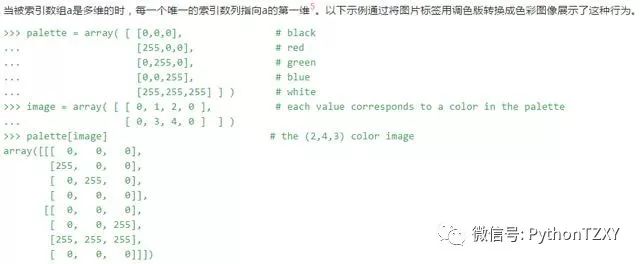
第二种通过布尔来索引的方法更近似于整数索引；对数组的每个维度我们给一个一维布尔数组来选择我们想要的切片。

>>>
 a = arange(12).reshape(3,4)>>> b1 = array([False,True,True]) #
 first dim selection>>> b2 = array([True,False,True,False]) # 
second dim selection>>>>>> a[b1,:] # selecting 
rowsarray([[ 4, 5, 6, 7], [ 8, 9, 10, 11]])>>>>>> 
a[b1] # same thingarray([[ 4, 5, 6, 7], [ 8, 9, 10, 
11]])>>>>>> a[:,b2] # selecting columnsarray([[ 0, 2],
 [ 4, 6], [ 8, 10]])>>>>>> a[b1,b2] # a weird thing to
 doarray([ 4, 10])

注意一维数组的长度必须和你想要切片的维度或轴的长度一致，在之前的例子中，b1是一个秩为1长度为三的数组(a的行数)，b2(长度为4)与a的第二秩(列)相一致。7

ix_()函数

ix_ 函数可以为了获得多元组的结果而用来结合不同向量。例如，如果你想要用所有向量a、b和c元素组成的三元组来计算 a+b*c ：

>>>
 a = array([2,3,4,5])>>> b = array([8,5,4])>>> c = 
array([5,4,6,8,3])>>> ax,bx,cx = ix_(a,b,c)>>> 
axarray([[[2]], [[3]], [[4]], [[5]]])>>> bxarray([[[8], [5], 
[4]]])>>> cxarray([[[5, 4, 6, 8, 3]]])>>> ax.shape, 
bx.shape, cx.shape((4, 1, 1), (1, 3, 1), (1, 1, 5))>>> result =
 ax+bx*cx>>> resultarray([[[42, 34, 50, 66, 26], [27, 22, 32, 
42, 17], [22, 18, 26, 34, 14]], [[43, 35, 51, 67, 27], [28, 23, 33, 43, 
18], [23, 19, 27, 35, 15]], [[44, 36, 52, 68, 28], [29, 24, 34, 44, 19],
 [24, 20, 28, 36, 16]], [[45, 37, 53, 69, 29], [30, 25, 35, 45, 20], 
[25, 21, 29, 37, 17]]])>>> result[3,2,4]17>>> 
a[3]+b[2]*c[4]17

你也可以实行如下简化：

def ufunc_reduce(ufct, *vectors): vs = ix_(*vectors) r = ufct.identity for v in vs: r = ufct(r,v) return r

然后这样使用它：

>>>
 ufunc_reduce(add,a,b,c)array([[[15, 14, 16, 18, 13], [12, 11, 13, 15, 
10], [11, 10, 12, 14, 9]], [[16, 15, 17, 19, 14], [13, 12, 14, 16, 11], 
[12, 11, 13, 15, 10]], [[17, 16, 18, 20, 15], [14, 13, 15, 17, 12], [13,
 12, 14, 16, 11]], [[18, 17, 19, 21, 16], [15, 14, 16, 18, 13], [14, 13,
 15, 17, 12]]])

这个reduce与ufunc.reduce(比如说add.reduce)相比的优势在于它利用了广播法则，避免了创建一个输出大小乘以向量个数的参数数组。8

用字符串索引

参见RecordArray。

线性代数

继续前进，基本线性代数包含在这里。

简单数组运算

参考numpy文件夹中的linalg.py获得更多信息

>>>
 from numpy import *>>> from numpy.linalg import *>>> a
 = array([[1.0, 2.0], [3.0, 4.0]])>>> print a[[ 1. 2.][ 3. 
4.]]>>> a.transpose()array([[ 1., 3.], [ 2., 4.]])>>> 
inv(a)array([[-2. , 1. ], [ 1.5, -0.5]])>>> u = eye(2) # unit 
2x2 matrix; "eye" represents "I">>> uarray([[ 1., 0.], [ 0., 
1.]])>>> j = array([[0.0, -1.0], [1.0, 0.0]])>>> dot 
(j, j) # matrix productarray([[-1., 0.], [ 0., -1.]])>>> 
trace(u) # trace2.0>>> y = array([[5.], [7.]])>>> 
solve(a, y)array([[-3.], [ 4.]])>>> eig(j)(array([ 0.+1.j, 
0.-1.j]),array([[ 0.70710678+0.j, 0.70710678+0.j], [ 
0.00000000-0.70710678j, 0.00000000+0.70710678j]]))Parameters: square 
matrixReturns The eigenvalues, each repeated according to its 
multiplicity. The normalized (unit "length") eigenvectors, such that the
 column ``v[:,i]`` is the eigenvector corresponding to the eigenvalue 
``w[i]`` .

矩阵类

这是一个关于矩阵类的简短介绍。

>>> A = 
matrix('1.0 2.0; 3.0 4.0')>>> A[[ 1. 2.][ 3. 4.]]>>> 
type(A) # file where class is defined>>> A.T # transpose[[ 1. 
3.][ 2. 4.]]>>> X = matrix('5.0 7.0')>>> Y = 
X.T>>> Y[[5.][7.]]>>> print A*Y # matrix 
multiplication[[19.][43.]]>>> print A.I # inverse[[-2. 1. ][ 
1.5 -0.5]]>>> solve(A, Y) # solving linear 
equationmatrix([[-3.], [ 4.]])

索引：比较矩阵和二维数组

注意NumPy中数组和矩阵有些重要的区别。NumPy提供了两个基本的对象：一个N维数组对象和一个通用函数对象。其它对象都是建构在它们之上的。特别的，矩阵是继承自NumPy数组对象的二维数组对象。对数组和矩阵，索引都必须包含合适的一个或多个这些组合：整数标量、省略号 (ellipses)、整数列表;布尔值，整数或布尔值构成的元组，和一个一维整数或布尔值数组。矩阵可以被用作矩阵的索引，但是通常需要数组、列表或者其它形式来完成这个任务。

现在有些和Python索引不同的了：你可以同时使用逗号分割索引来沿着多个轴索引。

>>> print A[:,1]; print A[:,1].shape[1 5 9](3,)>>> print M[:,1]; print M[:,1].shape[[1][5][9]](3, 1)

>>> A[:,[1,3]]array([[ 1, 3], [ 5, 7], [ 9, 11]])

稍微复杂点的方法是使用 take() 方法(method):

>>> A[:,].take([1,3],axis=1)array([[ 1, 3], [ 5, 7], [ 9, 11]])

如果我们想跳过第一行，我们可以这样：

>>> A[1:,].take([1,3],axis=1)array([[ 5, 7], [ 9, 11]])

或者我们仅仅使用 A[1:,[1,3]] 。还有一种方法是通过矩阵向量积(叉积)。

>>> A[ix_((1,2),(1,3))]array([[ 5, 7], [ 9, 11]])

为了读者的方便，在次写下之前的矩阵：

>>> A[ix_((1,2),(1,3))]array([[ 5, 7], [ 9, 11]])

现在让我们做些更复杂的。比如说我们想要保留第一行大于1的列。一种方法是创建布尔索引：

>>>
 A[0,:]>1array([False, False, True, True], dtype=bool)>>> 
A[:,A[0,:]>1]array([[ 2, 3], [ 6, 7], [10, 11]])

就是我们想要的！但是索引矩阵没这么方便。

>>> M[0,:]>1matrix([[False, False, True, True]], dtype=bool)>>> M[:,M[0,:]>1]matrix([[2, 3]])

技巧和提示

下面我们给出简短和有用的提示。

“自动”改变形状

更改数组的维度，你可以省略一个尺寸，它将被自动推导出来。

>>>
 a = arange(30)>>> a.shape = 2,-1,3 # -1 means "whatever is 
needed">>> a.shape(2, 5, 3)>>> aarray([[[ 0, 1, 2], [ 
3, 4, 5], [ 6, 7, 8], [ 9, 10, 11], [12, 13, 14]], [[15, 16, 17], [18, 
19, 20], [21, 22, 23], [24, 25, 26], [27, 28, 29]]])

2　NumPy-快速处理数据

标准安装的Python中用列表(list)保存一组值，可以用来当作数组使用，不过由于列表的元素可以是任何对象，因此列表中所保存的是对象的指针。这样为了保存一个简单的[1,2,3]，需要有3个指针和三个整数对象。对于数值运算来说这种结构显然比较浪费内存和CPU计算时间。

此外Python还提供了一个array模块，array对象和列表不同，它直接保存数值，和C语言的一维数组比较类似。但是由于它不支持多维，也没有各种运算函数，因此也不适合做数值运算。

NumPy的诞生弥补了这些不足，NumPy提供了两种基本的对象：ndarray（N-dimensional array object）和 ufunc（universal function object）。ndarray(下文统一称之为数组)是存储单一数据类型的多维数组，而ufunc则是能够对数组进行处理的函数。

数组的大小可以通过其shape属性获得：

>>> a.shape(4,)>>> c.shape(3, 4)

数组a的shape只有一个元素，因此它是一维数组。而数组c的shape有两个元素，因此它是二维数组，其中第0轴的长度为3，第1轴的长度为4。还可以通过修改数组的shape属性，在保持数组元素个数不变的情况下，改变数组每个轴的长度。下面的例子将数组c的shape改为(4,3)，注意从(3,4)改为(4,3)并不是对数组进行转置，而只是改变每个轴的大小，数组元素在内存中的位置并没有改变：

数组的元素类型可以通过dtype属性获得。上面例子中的参数序列的元素都是整数，因此所创建的数组的元素类型也是整数，并且是32bit的长整型。可以通过dtype参数在创建时指定元素类型:

>>>
 np.array([[1, 2, 3, 4],[4, 5, 6, 7], [7, 8, 9, 10]], 
dtype=np.float)array([[ 1., 2., 3., 4.], [ 4., 5., 6., 7.], [ 7., 8., 
9., 10.]])>>> np.array([[1, 2, 3, 4],[4, 5, 6, 7], [7, 8, 9, 
10]], dtype=np.complex)array([[ 1.+0.j, 2.+0.j, 3.+0.j, 4.+0.j], [ 
4.+0.j, 5.+0.j, 6.+0.j, 7.+0.j], [ 7.+0.j, 8.+0.j, 9.+0.j, 10.+0.j]])

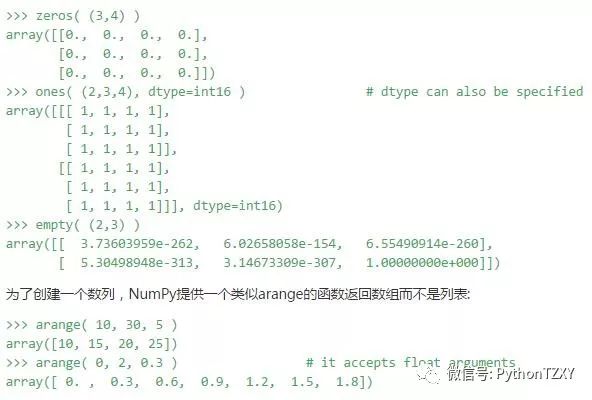
上面的例子都是先创建一个Python序列，然后通过array函数将其转换为数组，这样做显然效率不高。因此NumPy提供了很多专门用来创建数组的函数。下面的每个函数都有一些关键字参数，具体用法请查看函数说明。

arange函数类似于python的range函数，通过指定开始值、终值和步长来创建一维数组，注意数组不包括终值:
```
>>> np.arange(0,1,0.1)array([ 0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
```
linspace函数通过指定开始值、终值和元素个数来创建一维数组，可以通过endpoint关键字指定是否包括终值，缺省设置是包括终值:
```
>>>
 np.linspace(0, 1, 12)array([ 0. , 0.09090909, 0.18181818, 0.27272727, 
0.36363636, 0.45454545, 0.54545455, 0.63636364, 0.72727273, 0.81818182, 
0.90909091, 1. ])
```

logspace函数和linspace类似，不过它创建等比数列，下面的例子产生1(10^0)到100(10^2)、有20个元素的等比数列:

>>>
 np.logspace(0, 2, 20)array([ 1. , 1.27427499, 1.62377674, 2.06913808, 
2.6366509 , 3.35981829, 4.2813324 , 5.45559478, 6.95192796, 8.8586679 , 
11.28837892, 14.38449888, 18.32980711, 23.35721469, 29.76351442, 
37.92690191, 48.32930239, 61.58482111, 78.47599704, 100. ])

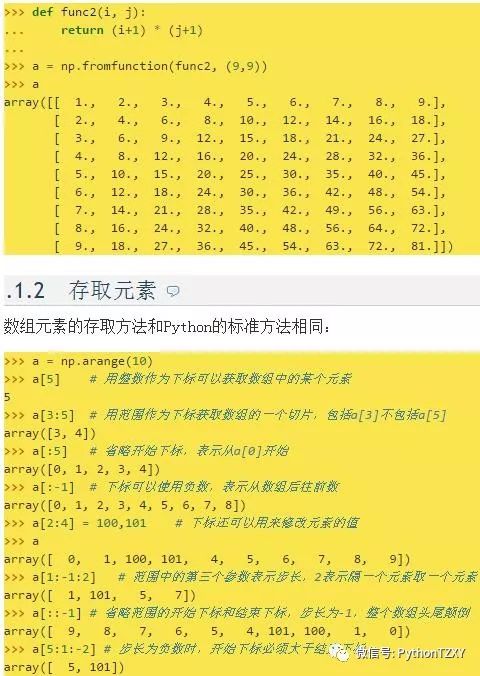
使用布尔数组

当使用布尔数组b作为下标存取数组x中的元素时，将收集数组x中所有在数组b中对应下标为True的元素。使用布尔数组作为下标获得的数组不和原始数组共享数据空间，注意这种方式只对应于布尔数组，不能使用布尔列表。

.1.3　多维数组

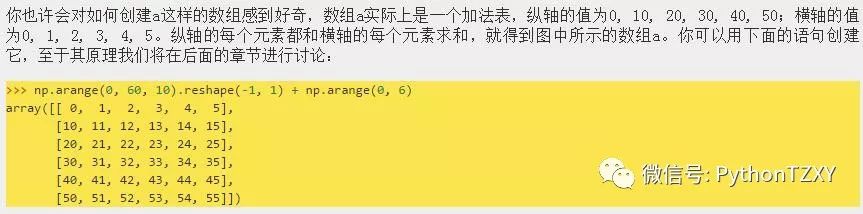
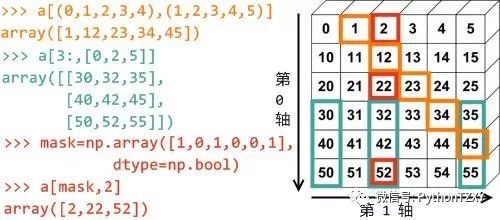
多维数组的存取和一维数组类似，因为多维数组有多个轴，因此它的下标需要用多个值来表示，NumPy采用组元(tuple)作为数组的下标。如图2.1所示，a为一个6x6的数组，图中用颜色区分了各个下标以及其对应的选择区域。

组元不需要圆括号

虽然我们经常在Python中用圆括号将组元括起来，但是其实组元的语法定义只需要用逗号隔开即可，例如 x,y=y,x 就是用组元交换变量值的一个例子。

a[(0,1,2,3,4),(1,2,3,4,5)] : 用于存取数组的下标和仍然是一个有两个元素的组元，组元中的每个元素都是整数序列，分别对应数组的第0轴和第1轴。从两个序列的对应位置取出两个整数组成下标： a[0,1], a[1,2], ..., a[4,5]。
a[3:, [0, 2, 5]] : 下标中的第0轴是一个范围，它选取第3行之后的所有行；第1轴是整数序列，它选取第0, 2, 5三列。
a[mask, 2] : 下标的第0轴是一个布尔数组，它选取第0，2，5行；第1轴是一个整数，选取第2列。

2.1.4　结构数组

在C语言中我们可以通过struct关键字定义结构类型，结构中的字段占据连续的内存空间，每个结构体占用的内存大小都相同，因此可以很容易地定义结构数组。和C语言一样，在NumPy中也很容易对这种结构数组进行操作。只要NumPy中的结构定义和C语言中的定义相同，NumPy就可以很方便地读取C语言的结构数组的二进制数据，转换为NumPy的结构数组。

假设我们需要定义一个结构数组，它的每个元素都有name, age和weight字段。在NumPy中可以如下定义

内存对齐

C语言的结构体为了内存寻址方便，会自动的添加一些填充用的字节，这叫做内存对齐。例如如果把下面的name[32]改为name[30]的话，由于内存对齐问题，在name和age中间会填补两个字节，最终的结构体大小不会改变。因此如果numpy中的所配置的内存大小不符合C语言的对齐规范的话，将会出现数据错位。为了解决这个问题，在创建dtype对象时，可以传递参数align=True，这样numpy的结构数组的内存对齐和C语言的结构体就一致了。

用下面的字典参数也可以定义结构类型，字典的关键字为结构中字段名，值为字段的类型描述，但是由于字典的关键字是没有顺序的，因此字段的顺序需要在类型描述中给出，类型描述是一个组元，它的第二个值给出字段的字节为单位的偏移量，例如age字段的偏移量为25个字节：

>>> np.dtype({'surname':('S25',0),'age':(np.uint8,25)})dtype([('surname', '|S25'), ('age', '|u1')])

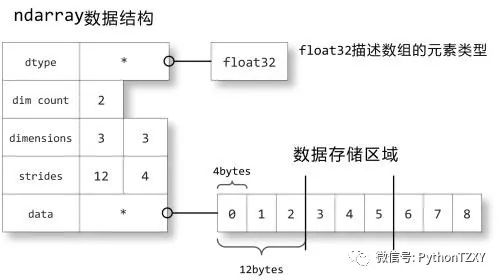
2.1.5　内存结构

下面让我们来看看ndarray数组对象是如何在内存中储存的。如图2.3所示，关于数组的描述信息保存在一个数据结构中，这个结构引用两个对象：一块用于保存数据的存储区域和一个用于描述元素类型的dtype对象。

sin函数的第二个参数也是x，那么它所做的事情就是对x中的每给值求正弦值，并且把结果保存到x中的对应的位置中。此时函数的返回值仍然是整个计算的结果，只不过它就是x，因此两个变量的id是相同的(变量t和变量x指向同一块内存区域)。

我用下面这个小程序，比较了一下numpy.math和P

ython标准库的math.sin的计算速度：:

请注意numpy.sin的计算速度只有math.sin的1/5。这是因为numpy.sin为了同时支持数组和单个值的计算，其C语言的内部实现要比math.sin复杂很多，如果我们同样在Python级别进行循环的话，就会看出其中的差别了。此外，numpy.sin返回的数的类型和math.sin返回的类型有所不同，math.sin返回的是Python的标准float类型，而numpy.sin则返回一个numpy.float64类型：

Python最牛逼数据分析库！月薪35K大牛：整理的NumPy详细教程！

正文

2 NumPy-快速处理数据

请到「今天看啥」查看全文

2　NumPy-快速处理数据