所谓“数值表”,也可以理解成“收藏夹”。人们在数学计算的过程中,如果得到了重要的结论,就把它们记录下来。久而久之,积累形成一张表,就叫数值表。下次遇到类似问题的时候,我们就不必再次计算了,直接查表便可以得到结果。
在我们的日常生活中,数值表无处不在。比如说个最简单的。九九乘法表,就是一张数值表。
只不过九九乘法表实在太简单了,似乎其中的每一个结论都是天造地设,天经地义的。所以我们经常意识不到,表中的那
45
个等式,它们本身就是重要的计算成果。
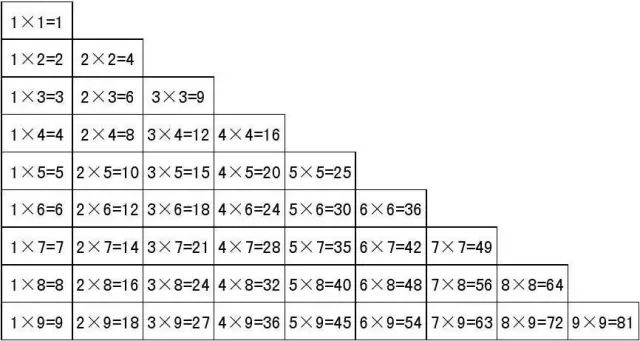
九九乘法表是怎么来的呢?当然不是天上掉下来的。而是用加法一步一步推出来的。
我们以幼教为例。假如幼儿背到“四六二十四”卡壳了,那么这时候不妨让他们从“一六得六”开始,“二六”,“三六”地顺序念下去。这样一来,等于是把乘法分解成多次加法。让他们把“四六二十四”这个结论,重新推导一遍。
经过多次重复之后,幼儿便把这个结果记到了心里。而这个过程,恰恰是数值表的本意。只不过许多人成年之后,就把当初的经历给忘记了。
九九乘法表虽然只有
45
句话,但是它的意义并不是点状的,一句话只能解决一个具体运算。实际上,它里面的每一句话,都是一条速算捷径。
比如说
49*7
=?严格地说,这是求
7
的
3
次方,如果我们背过立方表的话,就知道它等于
343
。但是绝大多数人看到这个式子,都会不由自主地念到“五七三十五”,从而猜到它的值在
350
左右。
为什么会这样呢?因为九九乘法表的结论在我们的脑海中已经根深蒂固了。所以我们愿意对问题进行一些近似,从而把它归纳到九九乘法表中现成的形式。这样就可以得到迅速的解答。
当然,走捷径肯定要承担一定的误差。这就好像我们开车,有的时候为了上高速,需要绕一段远路。关键是算总账,看合不合算。
所以说,数值表原本只是对先前计算结果的被动记录。但是当它被归纳整理,成熟到一定程度时,又会反过来形成“路径依赖”,影响我们将来处理问题的方法。这是一个非常有意思的现象。
相传在春秋时代,齐桓公招贤纳士,很久都没有人应聘。这时有个老头前来晋见,献“九九”之术。也就是说,他自称会背九九乘法表,想凭这个当官。
齐桓公说你这个本事好像不够格吧。老头说,如果我本事小,你也很重视。那么本事大的人听说了,肯定会加倍积极。齐桓公觉得有理,于是就款待了这个老头。这件事传开之后,四方贤士因此云集到齐国。
这个故事跟“千金买骨”的典故很像。不过从史料的角度看,它可以说明九九乘法表在春秋时代的地位。
一方面,九九乘法在当年肯定已经不算什么高深的学问了。但是另一方面,它也还没有普及到尽人皆知的地步。所以那个老头还可以凭它捞一顿饭吃吃。如果他只知道
1+1
=
2
就来应聘,那恐怕只能吃一顿板子罢了。
放眼全球,九九乘法表远远不是最早的数值表。比齐桓公还要再早上千年,两河流域的巴比伦人,就已经编制出了好多数值表。比如下面这张,就是“翻倍表”。它给出了
1
到
20
,以及
30
、
40
、
50
,这些数字翻倍之后的值。答案从
2
到
100
不等。
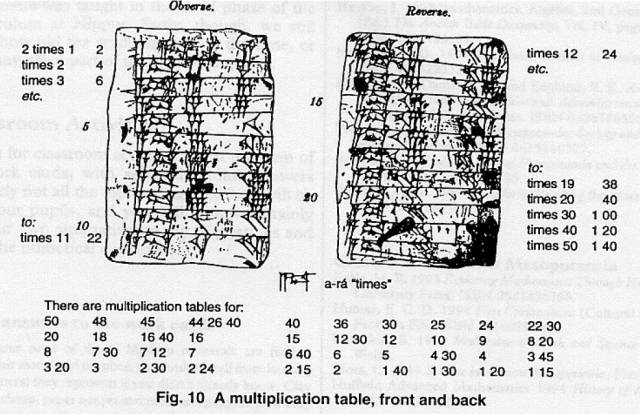
我们在《数字符号与古代文明》一节中介绍过,两河流域采用的数字符号体系,是最早由苏美尔人建立的“模糊位值制”。所以有很多我们现在觉得显而易见的答案,在当时计算起来还是有点小困难的。
比如说
6
的翻倍是
12
。要把
12
表达出来,先要把
10
个下三角进位成
1
个左三角,然后再加上
2
个下三角,这样就是
10+2
=
12
。
再比如
50
的翻倍是
100
。这时候
6
个左三角要进位到整个数位的左边,写
1
个下三角,然后再在原位写
4
个左三角,这样就是
1*60+40
=
100
。
从这里我们就可以看出,符号体系的对数学的影响是多么深刻。当然,巴比伦人的数学水平绝对不止于“翻倍表”这种小儿科而已。我们再看看下面这张“除数表”。
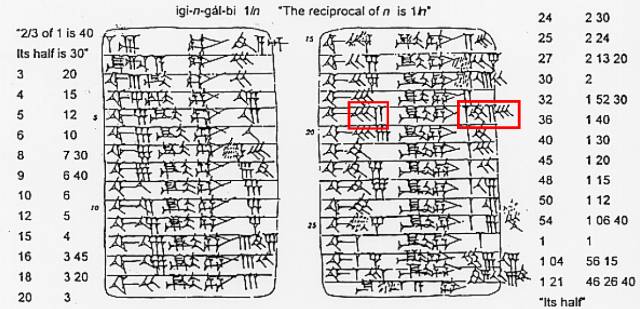
这张“除数表”给出了
60
除以各个数字得到的分数值。比如
60/3=20
,
60/4=15
,
60/5
=
10
,一直到
60/54=1.1111
,
60/64=0.9375
。
这些计算就有点难度了。如果必须使用楔形文字来演算的话,即使是受过良好教育的现代人,也未必能够算得非常清楚。
对巴比伦人来说,手边常备这么一张数值表,做算术的时候肯定会轻松许多。所以这样一块记载了前人智慧的泥板,颇有一点武功秘籍的味道,价值是相当大的。
两河流域历代数学家的心血,就这样凝成一张张数值表,代代相传。直到亚历山大帝国横空出世,古希腊人把整个楔形文字的符号体系全部抛弃了。这些数值表也就一下子失去了意义,从此长眠地下。
同样的事情,在罗马帝国崩溃之后,又发生了一次。
当时古希腊数学的绝大部分成果,被交到了伊斯兰文明的手里。不过伊斯兰数学家对《几何原本》等理论著作的兴趣不大。他们最推崇的数学家叫托勒密。他们把托勒密文集称为
Megisti Syntaxis
,也就是“数学大全”。其中最令他们如获至宝的一篇东西,叫作《弦表》。
《弦表》受到欢迎是可以理解的。因为它是一张数值表,没有什么条条框框,满满的都是答案,直接拿去就可以用。
这种拿来主义的精神流传至今。
我们的现行初中数学课本里面,还有这张《弦表》。不信你可以去看,原封不动,一模一样。只不过改了个名字,叫作“三角函数表”。
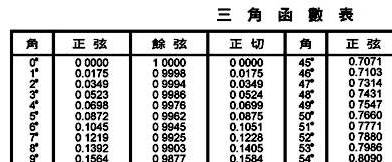
从内容上看,《弦表》记录了不同角度的正弦和余弦值。这些数据当时主要是用在天文学上面。当然,它里面的角度都是根据当时的度量体系,按照圆周
360
度来记录的。
大家千万不要小看了这张《弦表》。它的历史作用可大着呢。
从
罗马帝国到阿拉伯帝国,也算是改朝换代了。假如阿拉伯人提出,要改一个度量,把圆周分成
10
度,或者
100
度。行不行?从纯数学的角度看,这没什么大不了的,随时可行。
但是这样一来,《弦表》里面的数据就失效了,全部都要重算。所以如果你怕麻烦,想要继续使用《弦表》的话,那么你的度量体系就必须跟它保持一致,圆周必须是
360
度。
我们可以对比一下,
地中海世界的这2次数学文化传承。
因为古希腊人抛弃了巴比伦人的数字符号体系,所以巴比伦人在数值计算方面的宝贵积累全部都被废掉了。
比如对开根号的研究,巴比伦人很早就达到极高的成就。但是到了
1000
多年后的毕达哥拉斯时代,√
2
的计算居然又重新引起了轰动。这不是开历史的倒车吗?
风水轮流转。当伊斯兰文明取代古罗马的时候,正是为了继续使用那些数值表,充分享受前人的积累,所以便把先前符号体系的部分遗迹,也一并保留了下来。其中最显著的一个例子就是
60
进制。
这一保留,就一直流传到今天。对于现代人来说,时间和角度的
60
进制虽然显得有些格格不入。但是为了与过去的数据保持兼容,恐怕谁也不敢打它们的主意,想要去改弦更张。
这也是一种“路径依赖”。
伊斯兰数学家如此看重《弦表》,主要是用于天文学。古代人对于天文学的热情,现代人可能比较难以理解。
实际上,古代的观星术和占星术完全是两回事。拿天上的事情当幌子,说地上的事,那叫占星术。拿天上的事情说天上的事,就星论星,才叫观星术。
天上的星体运行,谁都看得到,没有任何遮掩和作弊的办法。说错了随时打脸。所以研究观星术,绝对是需要科学精神的。
观星术的实际用途,主要是两个方面。一是制定历法。这方面中国比较厉害。
在文艺复兴之前,古代历法的最高成就,来自元朝郭守敬的“四海测验”。
为了计算地球曲率对历法的影响,郭守敬设定了
27
个天文观测点。南起南海中沙群岛,北至西伯利亚通古斯河,纵跨
50
个纬度。如此壮举,想来也只有“大哉乾元”可以实现。
请注意,所有的历法,本质上都是数值表。
观星术的另一大用途就是航海导航。这方面一直是地中海世界领先。尤其是
1492
年哥伦布发现新大陆之后,欧洲人对天文观测的热情更是与日俱增。
在此后的
1
、
2
个世纪中,要论对欧洲天文学的贡献,大家熟知的哥白尼恐怕排不上第一。哥白尼出身名门,敢想敢说。但是他提出的日心说,实际上只是一个大胆的设想。既没有理论,也没有数据支持。所以在当时,他的观点并没有形成很大的影响,更没有受到后来布鲁诺那样残酷的教会压迫。
相比于轰轰烈烈的理论争鸣,欧洲天文学的真正突破来自于一条灰线。而这条灰线则发端于丹麦天文学家第谷。
第谷掌管着当时世界上最好的天文台。他用高超的观测技巧,积累了大量精确的天文数据。他的这些资料,最后整理出来就是一套数值表。因为天体运行是周期循环的。所以只要按照一项数据查表,就可以很容易地得到相应天体的其它数据。
我们说第谷的贡献是决定性的,但是他在科学史上的知名度却很低。这是因为他的研究成果,被他的天文台继任台长:开普勒,摘了桃子。
开普勒的名气就大多了。他的观测技巧不如第谷,但是数学知识很丰富。他的贡献在于,把第谷的海量观测数据总结成三个规律。后世称之为开普勒三大定律。
为了说明开普勒的工作内容,我们在这里举一个简化后的例子。比如说有一张数值表,它里面写明:
当
A
=
2
时,
B
=
4
;
当
A
=
3
时,
B
=
8
;
……
当
A
=
10
时,
B
=
1024
;
……
乍一看,
A
和
B
之间关系很凌乱。你只能老老实实地把它们列成一张表。需要计算的时候,挨个去查。
但是假如你熟悉指数函数,那么就很容易发现,其实
B
就等于
2
的
A
次方。于是你就不用啰里啰嗦地去记整张表了,直接用一个函数公式就可以表达它的全部内容了。这是数学史上的又一次飞跃。
开普勒的名气虽然很大,但是有一个人的名气比他还要大。那就是牛顿。在高中物理课上,我们都学过,开普勒三大定律和牛顿三大定律再加万有引力定律是等价的。
所谓等价,在数学上的意思就是说,牛顿定律不过是开普勒定律的另一种表述而已。内容没变,换个说法。
当然,我们这里绝对没有贬低牛顿的意思。万有引力定律的抽象程度比开普勒三大定律更高,数学推导也完善得多。但是它们的“合法性”基础是共同的。也就是说,你理论再好,大家凭什么相信你是对的?归根结蒂还是因为第谷的数值表。
人们用牛顿力学去套“金木水火土”五大行星的数据,都没有发现问题。但是天王星的观测数据与牛顿力学的计算不符。这怎么解释?















