前言
本文主要有两个目的:
-
-
学习如何扩展Pytorch算子,自己实现了一个能够forward和backward的卷积算子;
首先介绍了计算图的自动求导方法,然后对卷积运算中Kernel和Input的梯度进行了推导,之后基于Pytorch实现了卷积算子并做了正确性检验。
本文的代码在这个GitHub仓库:
https://github.com/dragonylee/myDL/blob/master/%E6%89%A9%E5%B1%95%E6%B5%8B%E8%AF%95.ipynb
。
计算图
计算图(Computational Graphs)是
torch.autograd
自动求导的理论基础,描述为一个有向无环图(DAG),箭头的方向是前向传播(forward)的方向,而逆向的反向传播(backward)的过程可以很方便地对任意变量求偏导。为了方便说明,这里举一个简单的例子:
其中
是输入,
是输出。
根据链式求导法则我们可得:
在Pytorch(Python)里定义上述三个函数:
def square(x):
return x ** 2
def mul3(x):
return x * 3
def mul_(x, y):
return x * y
然后用
torchviz
可视化其复合函数的计算图:
x = torch.tensor(3., requires_grad=True, dtype=torch.float)
y = torch.tensor(2., requires_grad=True, dtype=torch.float)
a = square(x) # a=x^2
b = mul3(a) # b=3a
c = mul_(b, y) # c=by
torchviz.make_dot(c, {"x": x, "y": y, "c": c}).view()
得到如下结果:
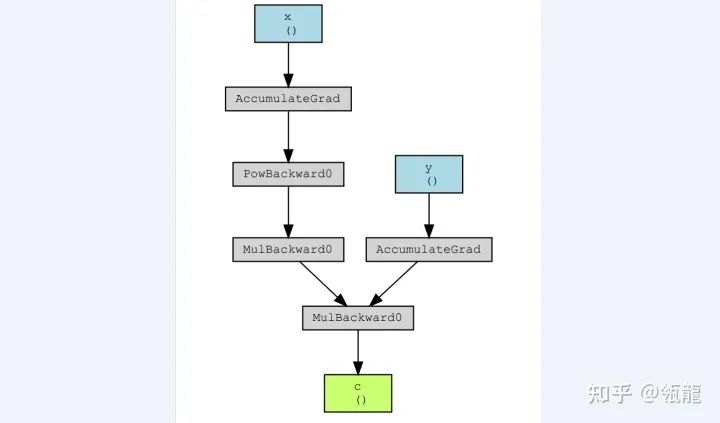
忽略“Accumulate”这个操作,在该计算图上的反向求导过程表示如下:
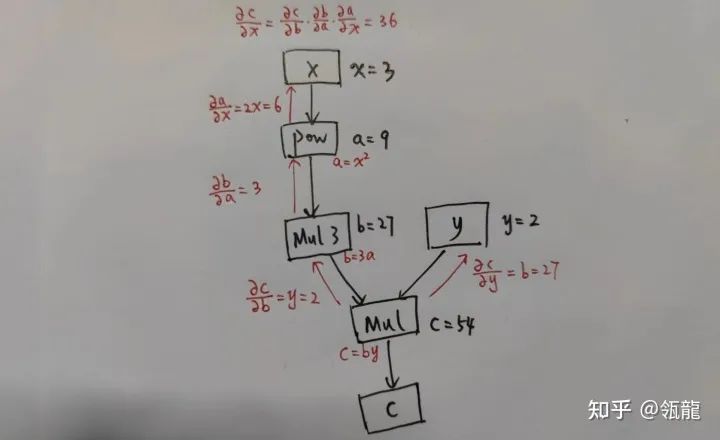
这很清晰地展示了计算图的功能,它记录了每一个变量(包括输出、中间变量)的计算函数(可以称之为一个
算子
,就是图中的方框,入边是输入,出边是输出),从而可以数值计算出相应的导数。实际上,任何变量qqq对ppp求导都可以对两者之间的反向链路进行累乘得到。
对输出
调用
.backward()
后,可以查看导数值:
c.backward()
print(y.grad)
print(x.grad)
输出结果和上图的计算结果一致。注意在backward过程中非叶子节点可以调用
.retain_grad()
来记录grad。
以前我一直以为自动求导是一个很复杂的操作,没想到一个计算图就非常简洁地实现了,才发现“我以为”的复杂操作其实是形式化的求导……
卷积运算与梯度推导
本文所涉及的卷积运算是最平凡的卷积运算,不包含stride, padding, dilation, bias等。定义卷积运算
Output
Input
Kernel,
其中
为输入, Kernel
为卷积 核, Output
Tensor
为输出, 且有
。
如何实现卷积?
可以先用
nn.Unfold
将输入的tensor展开,注意Unfold()也是可以指定stride, dilation等参数的,但我们这里不考虑这些,因此只用传入kernel_size,就可以将Input展开为Tensor
的形式。
input_unf = nn.Unfold(kernel_size=K)(input)
然后通过
view
将Input转变为Tensor
的形式。
input_unf = input_unf.view((B, Cin, -1, M, M))
同样通过
view
将Kernel转变为Tensor
的形式。
kernel_view = kernel.view((Cout, Cin, K * K))
而输出Output是Tensor
的形式。
在这里就可以直接用
Einstein求和标记
将卷积运算写出来了:

代码为
output = torch.einsum("ijklm,njk->inlm", input_unf, kernel_view)
如何计算梯度?
这部分求导的推导是我自己在草稿纸上完成的,后面经过一些验证应该或许可以保证是正确的。
为了能够用Pytorch自带的 gradcheck 来验证backward梯度计算的正确性, 我们有必要对每个输入参数都进行求导, 假设最终的Loss函数结果为
(是一个标量), 我们需要计算对输入Input的导数
以及对卷积核Kernel的导数
。
为了方便推导,先不考虑batch和channel,也就是Input, Kernel, Output都是二维的。
Kernel的梯度
根据链式求导法则我们可以将此导数(偏导)写作
式中
已知 (backward过程中会作为参数一直传下去),也就是计算图中当前卷积算子后面的链路所有梯度的累乘,其size与Output一致。
那么问题就是求Output对Kernel的偏导,我们用一个简单的例子来推导:
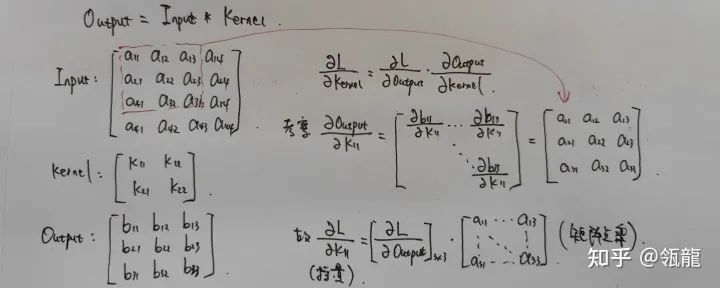
可以发现,
竟然就是
和Input矩阵的左上子矩阵的点积, 对于其它的
也是同理, 因此我们可以得到结论:
也就是说,Kernel的梯度,就是以Output的梯度作为卷积核,对Input卷积的结果。
Input的梯度
同样,Input的梯度可以写作
式中
已知, 同样沿用上面的例子来推导:

我们可以发现, 把
适当的0填充后, 以旋转
的Kernel做卷积运算, 就得到了
。公式可以写作( 可能不太规范 ):

因此Input的梯度计算方式可以表述为:Input的梯度, 就是以旋转180°的Kernel作为卷积核, 对
反卷积的结果。
自定义卷积算子
本文的一个很大目的,就是让我自己学会怎么扩展Pytorch的算子,从官方文档了解到,需要实现一个继承
torch.autograd.Function
的函数,并且实现
forward
和
backward
静态函数,才能适应Pytorch的自动求导框架,有一些需要注意的细节:
-
forward
和
backward
函数的第一个参数都是
ctx
,就是context的意思,与
self
类似,一般如果在backward过程中要用到forward的参数,在forward时就要调用
ctx.save_for_backward()
保存起来;
-
forward
有多少个输入,
backward
就要有多少个输出,这个看计算图就能明白了,如果不需要求梯度的入边,可以返回
None
;
梯度求解
前面在定义卷积运算时,都是考虑了Batch和Channel的,而在推导对Input和Kernel的梯度时,却为了方便没有考虑这两个参数。实际上在实现时,要特别注意每个数据的
view
的每个维度之间的关系。
例如我这里定义的:
Input : Tensor
Kernel: Tensor
Output: Tensor
在求Kernel的梯度时, 根据公式
Input
, 这里的维度是
Input: Tensor















