近日,有网友在知乎开帖,将自己总结的线性代数逻辑框架分享了出来,本来仅仅只是学习分享,没想到又又又把同济版线性代数拉出来鞭尸一回。
开帖如下:
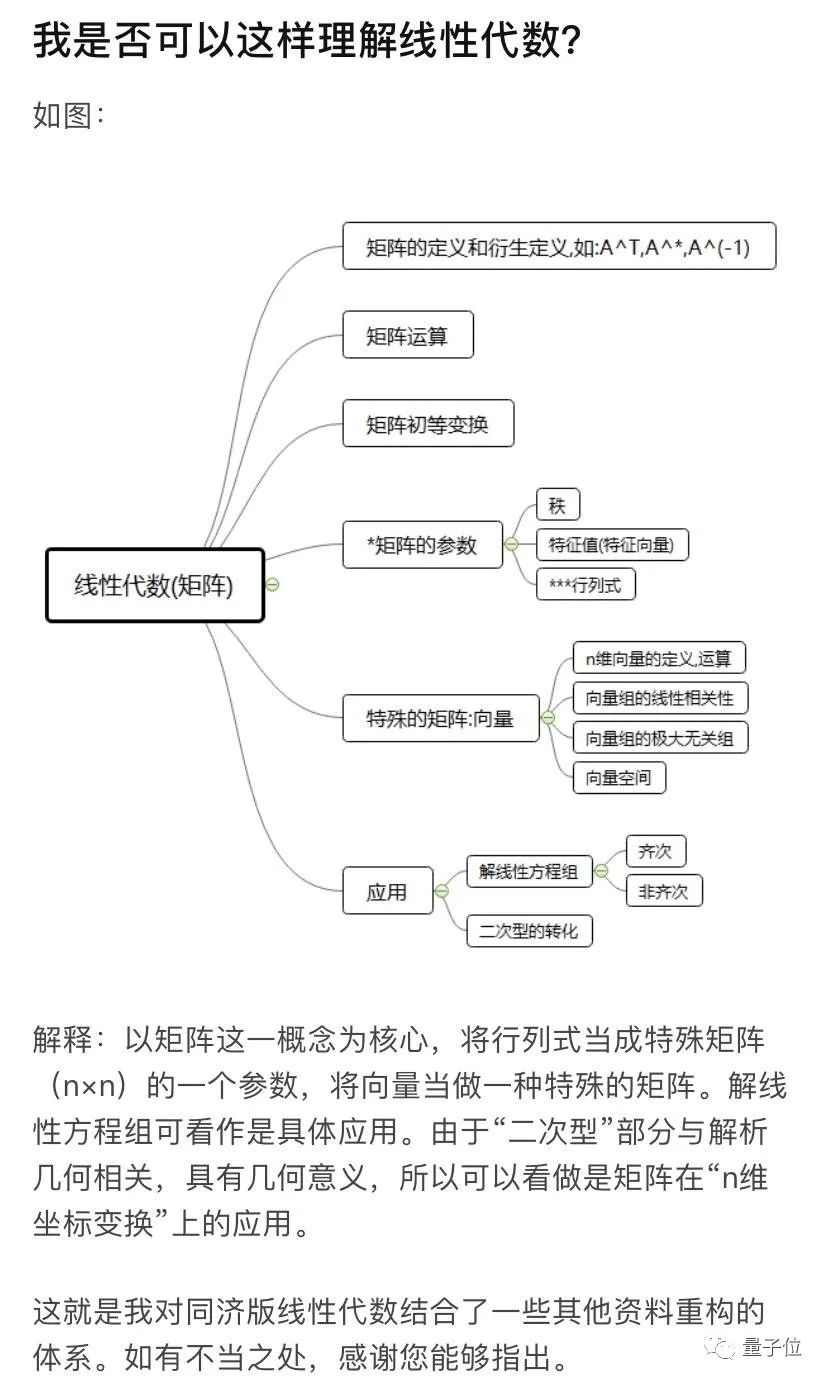
对于楼主的框架,广大网友表示不应该把矩阵作为理解线性代数的核心。
答主 @杨数森表示,线性代数的最核心问题就是
怎样的线性变换是相似的。

最好不要把矩阵作为线性代数的核心,就像不要把初等函数作为微积分的核心一样。
线性代数的最核心问题就是怎样的线性变换是相似的,而这些相似的线性变换具有怎样的特征。引入特征值为这个问题提供了巨大的帮助,却不够彻底,因为尚不能解释为何存在非零的幂零变换。
经过复杂的讨论,我们知道复线性变换的 Jordan 标准型是判断线性变换是否相似的标志,也是衡量线性变换的特征的方式。
所谓两个线性变换是相似的,就是它们能在适当的基下表示成相同的矩阵,而 Jordan 标准型就是其中的代表。
为了把线性代数应用到分析和几何领域,需要在线性空间中引入度量,而内积正是确定度量的巧妙方法。
欧氏空间是带有内积的线性空间,其中的内积是正定、对称的双线性函数。在有限维欧氏空间中,能够顺应所给内积的基是标准正交基,保持内积不变的变换是正交变换。欧氏空间中的另一个有意义的变换是对称变换,而它也恰好对应于二次型。
也有网友认为,向量空间、线性空间以及线性空间之间的态射应该是线性代数的核心。

更有网友表示,之所以会产生这样的误解,很大原因是
教材的编写框架
对人造成了误导。
同济版《线性代数》再一次被推到了风口浪尖。
同济版《线性代数》为何会引起众怒?
同济版《线性代数》为何会频频引起 “众怒” 呢?
早在 2019 年,知乎上便有了关于这版教材的
吐槽
讨论。
吐槽理由主要在于教材章节混杂、原理晦涩难懂,往往学完一本书也不明所以。
最令人诟病的便是
教材内容编排不合理
,无论是从行列式开始、还是从矩阵入手,教材开篇生硬地引入大量全新的概念,对于广大学子而言都深感莫名其妙。

尽管学习了行列式,但是大家行列式的认识也只停留在盲目做习题这一层面,把这行乘一个系数加到另一行上,再把另一行减过来,但是却不明白这么来回折腾的意义是什么。
此外,作为一门本身就十分抽象的学科,同济版《线性代数》对于许多概念的解释仍旧是冗长的下定义模式,缺乏直观的几何理解,这也使许多人更加不理解学习线性代数的意义。
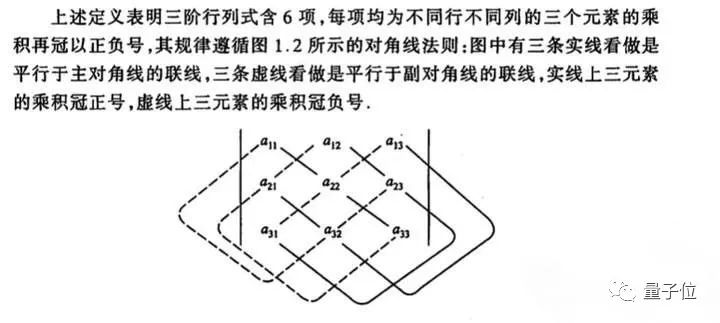
△
定义虽然讲解了对角线法则,但是却没有解释为什么四阶行列式开始便不使用该方法
不够合理的课程内容编排、晦涩难懂的定义原理,让人感觉这不是在学习一门课程,而是被不由分说地抛到一个强制的世界中,只是在考试的皮鞭下被迫赶路。
你的线性代数,之前可能都学错了
其实,同济版《线性代数》之所以会饱受吐槽,还有一个更大的原因:无论是科研还是实际工程应用,线性代数的身影无处不在。如果没有理解其中原理,在日后的运用中可谓是步履维艰。
CSDN 副总裁孟岩曾在《理解矩阵》一文中表示 “不少人即使能够很熟练地以线性代数为工具进行过科研和应用工作,但是对于很多初学者提出来的看上去很基础的问题并不清楚。”
比如说:矩阵究竟是什么东西?向量可以被认为是具有 n 个相互独立性质(维度)的对象的表示,矩阵又是什么呢?
如果认为矩阵是一组列(行)向量组成的新的复合向量的展开式,那么为什么这种展开式具有如此广泛的应用?
特别是为什么偏偏二维的展开式如此有用?如果矩阵中每一个元素又是一个向量,那么再展开一次,变成三维的立方阵,是不是更有用?

面对这一类的问题,许多老手们就好像大人在面对小孩子的刨根问底,最后总会迫不得已地说:“就是这么规定的,你接受并且记住就好。”
然而这样的问题如果不能获得回答,线性代数对于学习者而言就是一个简单粗暴的、莫名其妙的规则合集。












