2016全国高中数学联赛试题及评分标准

上海初高中数学 · 公众号 · 初高中 · 2017-08-23 19:04

正文

9月将至，开学的同时，每年一年一度的全国高中数学联赛也即将来了，同学们可知道高中联赛的前世今生吗？

从1956年起，在华罗庚、苏步青等老一辈数学家的倡导下，开始举办中学数学竞赛，在北京、上海、福建、天津、南京、武汉、成都等省市都开展了数学竞赛，并举办了由京、津、沪、粤、川、辽、皖合办的高中数学联赛。1979年，我国大陆上的29个省、市、自治区都举办了中学数学竞赛。

1980年，在大连召开的第一届全国数学普及工作会议上，确定将数学竞赛作为中国数学会及各省、市、自治区数学会的一项经常性工作，每年9月第二个星期日举行“全国高中数学联合竞赛”。

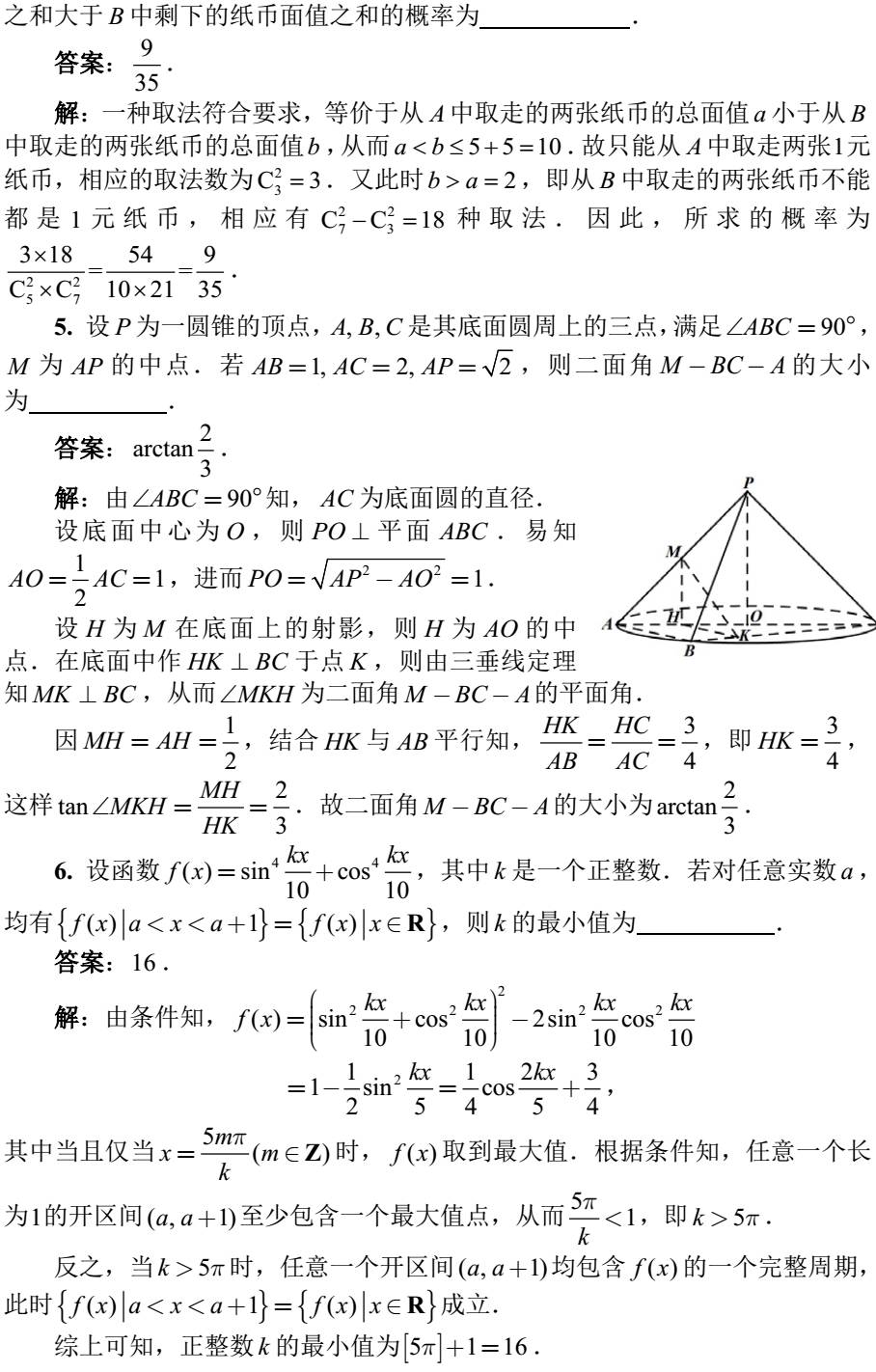
竞赛分为一试和二试，在这项竞赛中取得优异成绩的全国约200名学生有资格参加由中国数学会奥林匹克委员会主办的“中国数学奥林匹克( CMO )暨全国中学生数学冬令营”(每年元月)。各省的参赛名额由3人到8人不等，视该省当年的联赛考试成绩而定，且对于承办方省份有一定额外的优惠。在CMO中成绩优异的60名左右的学生可以进入国家集训队。经过集训队的选拔，将有6名表现最顶尖的选手进入中国国家代表队，参加国际数学奥林匹克( IMO )。

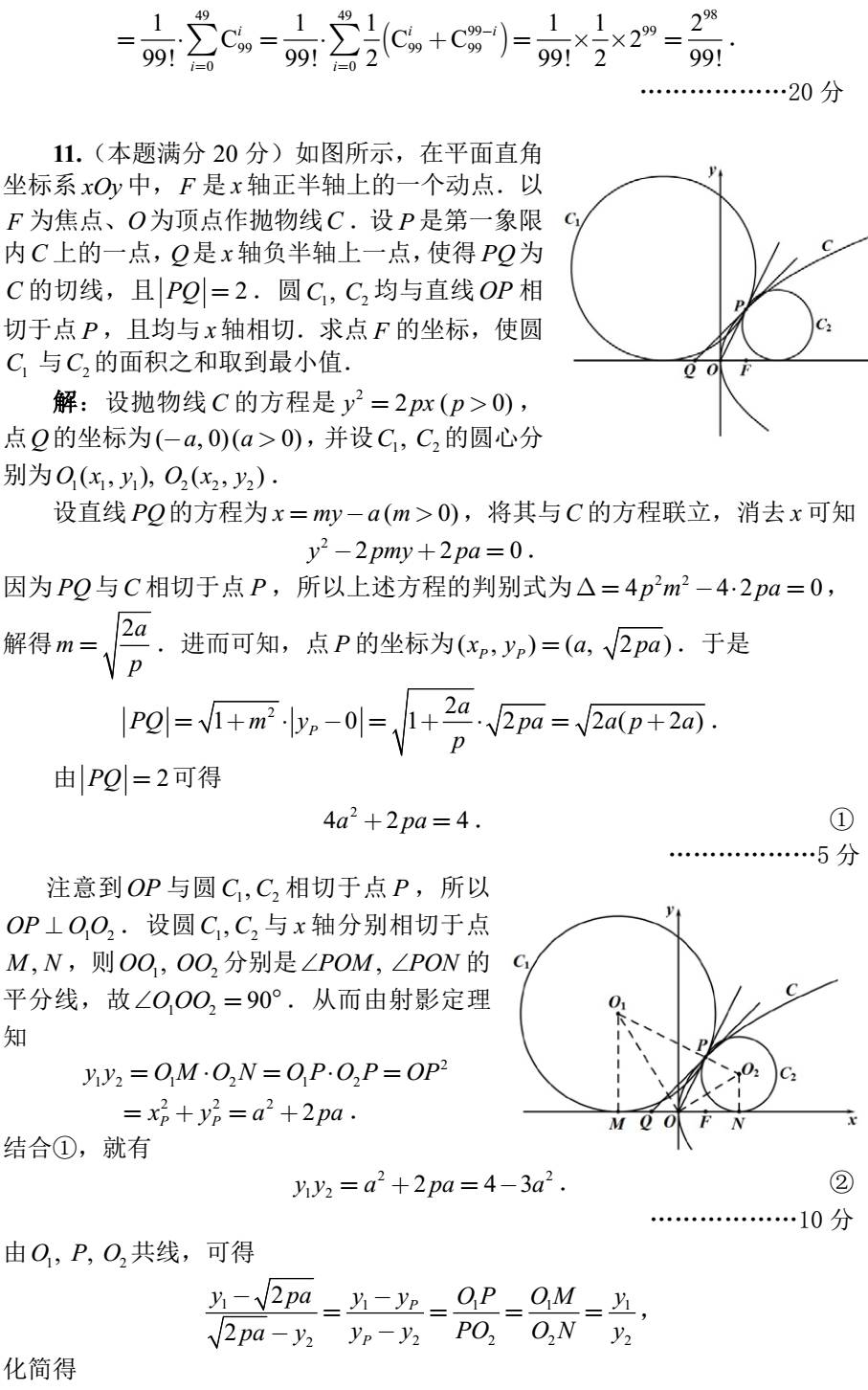
为了促进拔尖人才的尽快成长，教育部规定： 在高中阶段获得全国数学联赛省、市、自治区赛区一等奖者便获得保送重点大学的资格 ，对于没有保送者在高考中加分，加分情况根据各省市政策而定，有些省、市、自治区保留了竞赛获奖者高考加5分到20分不等，而部分省级行政区已经取消了竞赛加分。 对二、三等奖获得者，各省、市、自治区又出台了不同的政策，其中包括自主招生资格等优惠录取政策 。为严格标准，中国数学会每年限定一等奖名额1000名左右，并划分到各省、市、自治区。各省、市、自治区在上报一等奖候选人名单的同时，还要交上他们的试卷，最终由中国数学会对其试卷审核后确定获奖名单。

☆ 试题模式

自2010年起，全国高中数学联赛试题新规则如下：

联赛分为一试、加试（即俗称的“二试”）。各个省份自己组织的“初赛”、“初试”、“复赛”等等，都不是正式的全国联赛名称及程序。一试和加试均在每年10月中旬的第一个周日举行。

一试

考试时间为上午8：00-9：20，共80分钟。试题分填空题和解答题两部分，满分120分。其中填空题8道，每题8分；解答题3道，分别为16分、20分、20分。

加试（二试）

考试时间为9：40-12：10，共150分钟。试题为四道解答题，前两道每题40分，后两道每题50分，满分180分。试题内容涵盖平面几何、代数、数论、组合数学等。

依据考试结果评选出各省级赛区级一、二、三等奖。其中一等奖由各省负责阅卷评分，然后将一等奖的考卷寄送到主办方（当年的主办方），由主办方复评，最终由主管单位（中国科协）负责最终的评定并公布。二、三等奖由各个省自己决定。各省、市、自治区赛区一等奖排名靠前的同学可参加中国数学奥林匹克（CMO）。

☆ 知识范围

一试

全国高中数学联赛的一试竞赛大纲，完全按照全日制中学《数学教学大纲》中所规定的教学要求和内容，即高考所规定的知识范围和方法，在方法的要求上略有提高，其中概率和微积分初步不考。

加试（二试）

全国高中数学联赛(加试)在知识方面有所扩展，适当增加一些教学大纲之外的内容，所增加内容是：

1．平面几何

西姆松定理；三角形旁心、费马点、欧拉线；几何不等式；几何极值问题；几何中的变换：对称、平移、旋转；圆的幂和根轴；面积方法，复数方法，向量方法，解析几何方法。

2．代数

周期函数，带绝对值的函数；三角公式，三角恒等式，三角方程，三角不等式，反三角函数；递归，递归数列及其性质，一阶、二阶线性常系数递归数列的通项公式；第二数学归纳法；均值不等式，柯西不等式，排序不等式，切比雪夫不等式，一元凸函数及其应用；复数及其指数形式、三角形式，欧拉公式，棣莫弗定理，单位根；多项式的除法定理、因式分解定理，多项式的相等，整系数多项式的有理根*，多项式的插值公式*； n次多项式根的个数，根与系数的关系，实系数多项式虚根成对定理；函数迭代，求n次迭代*，简单的函数方程*。