如果你玩过MMOARPG游戏,比如魔兽,你会发现人物行走会很有趣,为了模仿人物行走的真实体验,他们会选择最近路线达到目的地,期间会避开高山或者湖水,绕过箱子或者树林,直到走到你所选定的目的地。
这种看似普通的路径在程序实现起来就需要一定的寻路算法来解决,如何在最短时间内找到一条路径最短的路线,这是寻路算法首先要考虑的问题。
在这篇文章中我们会循序渐进来讲解寻路算法是如何演进的,从文中你会看到一种算法从简单到高效所遇到的问题,以及,带着问题来阅读,理解更快。
本篇主要包含以下内容:
1、图
2、宽度最优搜索
3、Dijkstra 算法
4、贪心算法
5、A*搜索算法
6、B*搜索算法
你所看到的人物行走方式:

开发人员实际所看到的方式:
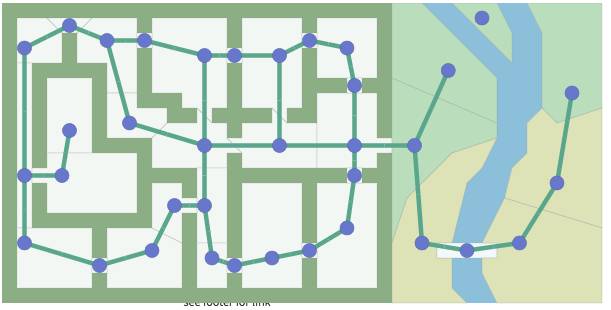
或者是这种:
对于一张地图,开发人员需要通过一定的方案将其转换为数据对象,常见的就是以上这种把地图切个成网格,当然了地图的划分方式不一定非要用网格这种方式,采用多边形方式也可以,这取决于你的游戏。
一般情况下,同等面积的地图采用更少的顶点,寻路算法会更快。寻路中常用的数据结构就是图,我们先来了解一下基础。
在讲寻路算法之前我们先了解一种数据结构—图,网格某种意义上也是图的演变,只是图形变了而已,理解了图的概念可以帮助我们更好理解寻路算法。
图的基本定义:
图的正式表达式是G=(V,E),V是代表顶点的集合,E和V是一种二元关系,可以理解为边,比如有条边从顶点U到顶点V结束,那么E可以用(u,v)来表示这条边。具体的有向图和无向图,也是边是否有方向来区分。
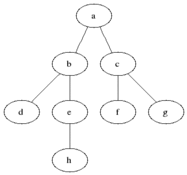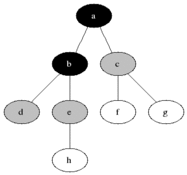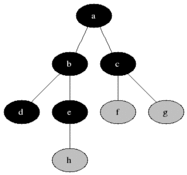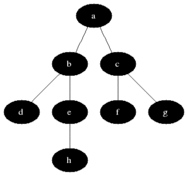
为了方便理解,我们文中所有的数据演示都是基于网格地图来进行讲解,以下是几种关系梳理,以A为顶点,BCDE为子顶点,我们可以把每个格子也看是一个顶点。
搜索算法:
对一个图进行搜索意味着按照某种特定的顺序依次访问其顶点。对于多图算法来说,广度优先算法和深度优先搜索算法都十分重要,因为它们提供了一套系统地访问图数据结构的方法。我们着重讲解广度优先搜索算法。
深度优先搜索:
深度优先算法和最小路径关系不大,我们只简单介绍。

深度优先搜索算法(简称DFS)是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点,尽可能深的搜索树的分支。

广度优先搜索算法(简称BFS)又称为宽度优先搜索,是一种图形搜索算法,是探讨最短路径的第一个模型,我们会顺着这个思路往下讲。
BFS是一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位址,彻底地搜索整张图,直到找到结果为止它的步骤如下:

- 首先将根节点放入队列中。
- 从队列中取出第一个节点,并检验它是否为目标。
- 如果找到目标,则结束搜寻并回传结果。
- 否则将它所有尚未检验过的直接子节点(邻节点)加入队列中。
- 若队列为空,表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。

网格:

我们看下代码(js):
var frontier = new Array();
frontier.put(start);
var visited = new Array();
visited[start] = true;
while(frontier.length>0){
current = frontier.get();
//查找周围顶点
for(next in graph.neighbors(current)){
var notInVisited = visited.indexOf(next)==-1;
//没有访问过
if(notInVisited) {
frontier.put(next);
visited[next] = true;
}
}
}
从上可以发现,宽度搜索就是以开始顶点为起点,访问其子节点(在网格中是访问周围节点),然后不断的循环这个过程,直到找到目标,这种算法比较符合常规逻辑,把所有的的顶点全部枚举一遍。不过这种方式也有很明显的缺点。
缺陷:
1、效率底下, 时间复杂度是:T(n) = O(n^2)
2、每个顶点之间没有权值,无法定义优先级,不能找到最优路线。比如遇到水域需要绕过行走,在宽度算法里面无法涉及。
如何解决这个问题?我们来看Dijkstra 算法。
宽度优先搜索算法,解决了起始顶点到目标顶点路径规划问题,但不是最优以及合适的,因为它的边没有权值(比如距离),路径无法进行估算比较最优解。
为何权值这么重要,因为真实环境中,2个顶点之间的路线并非一直都是直线,需要绕过障碍物才能达到目的地,比如森林,湖水,高山,都需要绕过而行,并非直接穿过。
比如我采用宽度优先算法,遇到如下情况,他会直接穿过障碍物(绿色部分 ),明显这个不是我们想要的结果:





