本节我们再谈置换矩阵与转置矩阵,并介绍对称阵。之后便进入学习线代的关键所在:向量空间与子空间。
所谓的置换矩阵 P,就是用来完成行交换的矩阵,更具体来讲,是行重新排列 了的单位矩阵。例如 I 就是一个置换矩阵,只不过 I 对矩阵没影响。
那么对于 n 阶矩阵来说,有多少个置换矩阵呢?答案是:n!种,也就是将单 位矩阵 I 各行重新排列后所有可能的情况数量。


在讲消元法的时候,主元位置为 0 是一件很让人头疼的事情,这时就需要置 换矩阵 P 来完成行交换,确保消元过程顺利进行。上节课学习 A = LU 分解时, 我们没有考虑要交换行的过程,如果我们想写出更普适的 LU 分解式的话,必须把行交换情况考虑进去,即:
PA = LU
先用行交换使得主元位置不为 0,行顺序正确。其后再用 LU 分解。
之前简单介绍过转置矩阵,即

对称矩阵,顾名思义,就是主对角线两侧元素对应相等的矩阵。或者说,对 矩阵 A,如果有:

首先明确“向量空间”的概念,它表示一整个空间的向量,但是要注意,不是任意向量的集合都能被称为向量空间。所谓的向量空间,必须满足一定规则, 就是:该空间对线性运算(相加,数乘)封闭。类似:v → 3v 或 v,w → v+w 运算,若得到的 3v 或者 v+w 都仍然在此空间中,那么这个空间可称为向量空间。
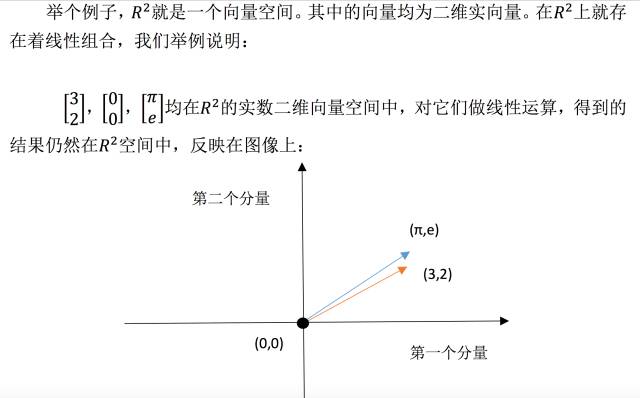

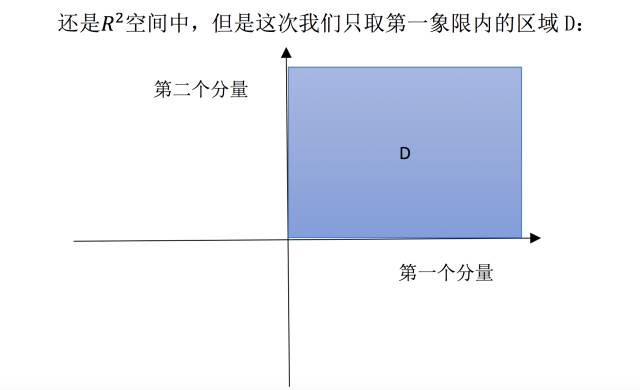
很明显,这部分空间无法满足“线性组合仍在空间中”的要求,比如数乘运算时,随便取个负数,向量就跑到第三象限去,脱离 D 空间范围内了。
上面的反例已经证明了。在向量空间里随便取其一部分,很可能得到的不是 向量空间。那如果我们取向量空间的一部分,将其打乱,构成的有没有可能是向 量空间呢?
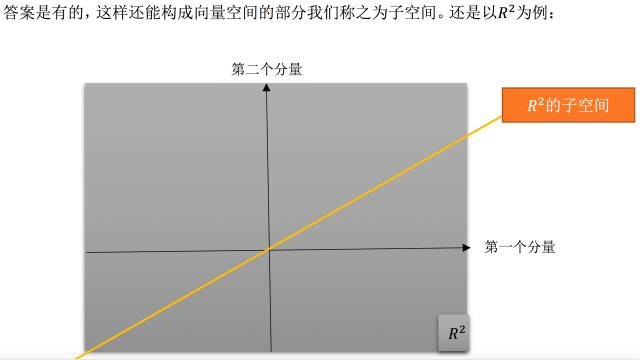

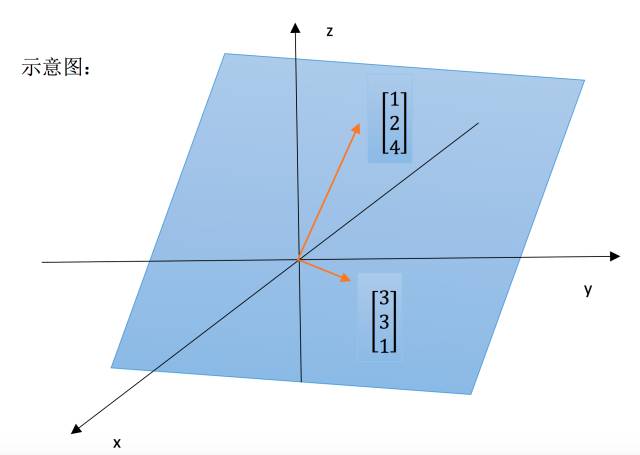
上面介绍的子空间都是基于已知的图像来寻找的,接下来我们来通过具体的 矩阵来构造出一个子空间,比如:列向量构造出的列空间。

转自:机器学习算法与自然语言处理




