
数据挖掘入门与实战 公众号: datadw
按照前面文章的方法进行数据预测,完全不使用POI,天气,交通情况的数据,可以达到0.43的成绩。
不过如果想要获得更好的成绩,简单的预测方法显然无法满足要求了。
GBDT
网友说可以使用GBDT的方法来进行数据预测。所以,我们先来聊聊GBDT算法的一些基础知识。
熵
凡是说到算法,人工智能,机器学习的文章,多半一定要说到 熵 这个概念的。什么是熵?
百度一下:
熵(entropy)指的是体系的混乱的程度,它在控制论、概率论、数论、天体物理、生命科学等领域都有重要应用,在不同的学科中也有引申出的更为具体的定义,是各领域十分重要的参量。熵由鲁道夫·克劳修斯(Rudolf
Clausius)提出,并应用在热力学中。后来在,克劳德·艾尔伍德·香农(Claude Elwood
Shannon)第一次将熵的概念引入到信息论中来。
一个体系越是单调,则熵越低,反之亦然。
这里我们引用数据挖掘大神的文章来接单说一下熵。
如果有一个字符串,里面包含了4种字符,每种出现的概率都是P= 1/4。
P(X=A) = 1/4
P(X=B) = 1/4
P(X=C) = 1/4
P(X=D) = 1/4
这样的字符串可能是:BAACBADCDADDDA。传送这样的字符串,每一个字符需要用几个bit?
答案是2个bit
A = 00, B = 01, C = 10, D =11
如果有一个字符串,里面包含了4种字符,但是每个字符串出现的概率不同
P(X=A) = 1/2
P(X=B) = 1/4
P(X=C) = 1/8
P(X=D) = 1/8
传送这样的字符串,每一个字符平均需要用几个bit?注意这里说平均。
答案是1.75个bit
A = 0, B = 10, C = 110, D =111
(如果使用等概率的方法, A = 00, B = 01, C = 10, D =11,则无法节省编码量,还是2个bit)
这里巧妙的做到了,出现概率高的字符,使用的bit位少,同时做到了编码上的问题。
(AB =〉010 和 C 110,D 111 不重复。AA =〉00 和 B 10 不重复 等)
有如果有一个字符串,里面3种字符串,每种出现概率都是 1/3呢?
最简单的编码方式是 A = 00, B = 01, C = 10, 这样是2个bit,但是如果好好计算一下,可以做到1.6个bit。
A=10,B= 11,C = 0(理论上是1.58496 个bit)
有如果有一个字符串,里面N种字符串,每种出现概率是 PN呢?
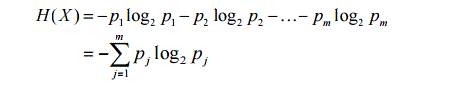
如果有一个字符串,里面包含了4种字符,每种出现的概率都是P= 1/4 = 0.25。
log(0.25,2) = - 2
H(X) = - (1/4) log(0.25,2) - (1/4) log(0.25,2) - (1/4) log(0.25,2) - (1/4) log(0.25,2) = 2;
如果要表示下图的H(X)和H(Y)呢?
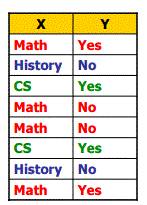
这个很容易计算
H(X)= 1.5
P(Math) = 1/2 P(History)= 1/4 P(CS)= 1/4
log(0.25,2) = - 2 log(0.5,2) = - 1
H(X) = - (1/2) log(0.5,2) - (1/4) log(0.25,2) - (1/4) * log(0.25,2) = 0.5 + 0.5 + 0.5 = 1.5;
H(Y)= 1
P(Yes) = 1/2 P(No) = 1/2
H(Y) = - (1/2) log(0.5,2) - (1/2) log(0.5,2) = 0.5 + 0.5 = 1;
如果说,我们的计算范围只是 X = Math 的数据。那么这个时候 H(Y | X = Math) 是多少呢?是多少呢?答案是1。(一共4条记录,但是Y有两种可能性)
如果说,我们的计算范围只是 X = Histroy 的数据。那么这个时候 H(Y| X = Histroy)是多少呢?答案也是 0 。(一共2条记录,但是Y只是一种可能性)
如果说,我们的计算范围只是 X = CS 的数据。那么这个时候 H(Y| X = CS)是多少呢?答案也是 0 。(一共2条记录,但是Y只是一种可能性)
H(Y | X ): 条件熵 Conditional Entropy
现在我们考虑一个问题,如果我们需要将Y传输出去。当然,如果直接传输的话, H(Y)= 1。
如果我们在传输的时候,双方都知道X的值,则需要熵定义为H(Y | X )。
例如:大家都知道X=History,则 Y 必然是 NO, H(Y ) = 0 , Histroy的可能性是1/4 ,需要的传输量是 0(CS同理)
大家都知道X=Math,则 Y 可能是 Yes或者No,H(Y ) = 1 ,Math的可能性是1/2 ,需要的平均传输率是 1/2 1 = 0.5
Math的概率 P(Math) = 1/2 ; History的概率 P(Histroy)= 1/4; History的概率 P(CS)= 1/4;
则我们定义H(Y | X ) = H(Y | X = Math) P(Math) + H(Y| X = Histroy) P(Histroy) + H(Y| X = CS) P(CS) = 0.5

Information Gain 信息增益 和 Relative Information Gain
从上文可知,比起直接传输Y,条件熵则更加划算了。这些划算的部分,我们称为信息增益IG。
IG(Y|X) = H(Y) - H(Y | X)
上面的例子,IG(Y|X) = H(Y) - H(Y | X) = 1 - 0.5 = 0.5
进一步,这样划算的部分,占原来所需部分的比重是多少呢?
RIG= IG(Y|X) / H(Y) = 0.5 / 1 = 0.5 (节省的部分占了50%)
信息增益是什么,我们先从它的用处来了解它:
信息增益是特征选择中的一个重要指标,它定义为一个特征能够为分类系统带来多少信息,带来的信息越多,该特征越重要。
离散化
回到滴滴算法的问题,我们应该挑选哪些指标作为GBDT的参考呢?
所有的这些指标在使用之前都进行一下离散化。
关于离散化的好处:数据处理:离散化好处多
http://blog.sina.com.cn/s/blog_652090850100ynds.html
例如,在滴滴算法大赛里面,天气中的PM值,交通拥堵状况都是一些具体的数值,这里用离散化后,才能放入决策树中。
GBDT实现(C#)
///
/// 回归分类树节点
///
class TreeNode
{
///
/// 节点属性名字
///
public string attrName { set; get; }
///
/// 节点索引标号
///
public int nodeIndex { set; get; }
///
/// 包含的叶子节点数
///
public int leafNum { set; get; }
///
/// 节点误差率
///
public double alpha { set; get; }
///
/// 父亲分类属性值
///
public string parentAttrValue { set; get; }
///
/// 孩子节点
///
public TreeNode[] childAttrNode { set; get; }
///
/// 数据记录索引
///
public List dataIndex { set; get; }
}
(隐)马尔可夫模型的思考
在滴滴算法问题中,你需要预测的是第4个时间片,前3个时间片的状态是已经知道的。
如果我们知道第一个时间片和第二个时间片的GAP是呈现上升或者持平或者下降的状态变化,记作 C1,第二和第三个时间片变化记作 C2。
是不是可以通过C1 ,C2 ,拟合出 C3呢?
社会工程学
在拟合的时候,不可避免的会考虑各种天气对于订单的影响,但是官方并没有给出天气的类型和天气描述之间的关系。
通过对于数据的分析,我们可以知道采样数据是来自上海市(感谢某位做天气研究的同学)
然后通过查阅历史资料,我们也可以初步获得所有天气类型值和天气描述的关系,这个是无法用程序和算法完成的,所以我认为这也是社会工程学的一部分。
public static string GetWeatherType(int type)
{
string des = "未知";
switch (type)
{
case 1:
des = "雾";
break;
case 2:
des = "晴";
break;
case 3:
des = "轻雾";
break;
case 4:
des = "降水";
break;
case 6:
//2016-01-22上海雨夹雪
des = "雪";
break;
case 8:
des = "雷暴";
break;
case 9:
des = "霾";
break;
default:
des = "未知";
break;
}
return des;
}
决策树(分类)
组委会是要求测算GAP值,是个定量问题。在这之前,我们看一下是否能够限定性分析一下GAP的高低呢?
从滴滴算法大赛的数据可以知道,数据的特征值大约有这些:
有一些特征需要自己去发现
整理出来的表格大概像这个样子的(不完全,示例)
| 天气类型 | 交通状态 | 工作日 | GAP分类 |
|---|
| 晴 | 拥挤 | 是 | 高 |
| 雷暴 | 轻度拥挤 | 否 | 低 |
| 晴 | 拥挤 | 否 | 中 |
| 雪 | 拥挤 | 否 | 中 |
| 晴 | 重度拥挤 | 是 | 高 |
这个时候,我们到底先用哪个条件作为优先决策的依据呢?答案就是上文提到的信息增益。
Information Gain 信息增益 和 Relative Information Gain
IG(GAP分类 | 天气类型) = H(GAP分类) - H(GAP分类 | 天气类型)
IG(GAP分类 | 交通状态) = H(GAP分类) - H(GAP分类 | 交通状态)
IG(GAP分类 | 工作日) = H(GAP分类) - H(GAP分类 | 工作日)
哪个数字最大就挑选哪个作为第一优先分类条件。
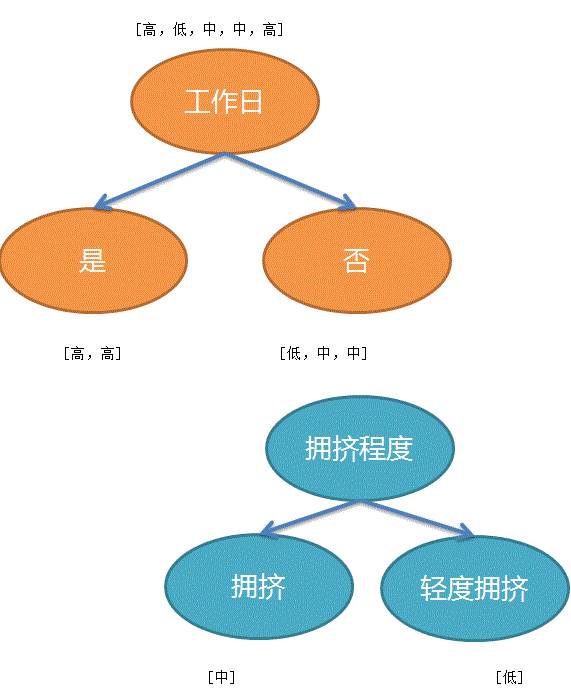
现在我们假设工作日是最高信息增益的,作为第一个决策条件
第一次分组之后就是这个样子了:
| 天气类型 | 交通状态 | 工作日 | GAP分类 |
|---|
| 晴 | 拥挤 | 是 | 高 |
| 晴 | 重度拥挤 | 是 | 高 |
| 天气类型 | 交通状态 | 工作日 | GAP分类 |
|---|
| 雷暴 | 轻度拥挤 | 节假日 | 低 |
| 晴 | 拥挤 | 否 | 中 |
| 雪 | 拥挤 | 否 | 中 |
按照理论(大神的文章,以后会翻译的),工作日组的GAP分类都一致了,所以就无需决策了。
对于节假日组,根据交通状态进行再分类
| 天气类型 | 交通状态 | 工作日 | GAP分类 |
|---|
| 雷暴 | 轻度拥挤 | 否 | 低 |
| 晴 | 拥挤 | 否 | 中 |
| 雪 | 拥挤 | 否 | 中 |
交通状态再分类结果如下
| 天气类型 | 交通状态 | 工作日 | GAP分类 |
|---|
| 晴 | 拥挤 | 否 | 中 |
| 雪 | 拥挤 | 否 | 中 |
这里无需天气类型就可以完成分类决策了。
(当然还有一种情况是所有特征都用完了,还是不能完全分类,这个时候可以使用多数表决的方式决定分类)
决策树(定量)
上面是一个定性的过程,下面我们来看一下,如果需要定量怎么处理呢?
| 天气类型 | 交通状态 | 工作日 | GAP数 |
|---|
| 晴 | 拥挤 | 是 | 893 |
| 雷暴 | 轻度拥挤 | 否 | 375 |
| 晴 | 拥挤 | 否 | 542 |
| 雪 | 拥挤 | 否 | 437 |
| 晴 | 重度拥挤 | 是 | 753 |
| 天气类型 | 交通状态 | 工作日 | GAP数 | 误差 |
|---|
| 晴 | 拥挤 | 是 | 893 | 293 |
| 雷暴 | 轻度拥挤 | 否 | 375 | 225 |
| 晴 | 拥挤 | 否 | 542 | 58 |
| 雪 | 拥挤 | 否 | 437 | 167 |
| 晴 | 重度拥挤 | 是 | 753 | 153 |
第一次分类怎么处理呢?
分裂的时候选取使得误差下降最多的分裂
如果我们选择工作日作为分裂条件
工作日的均值是:(893 + 753 )/ 2 = 823
| 天气类型 | 交通状态 | 工作日 | GAP数 | 误差 |
|---|
| 晴 | 拥挤 | 是 | 893 | +70 |
| 晴 | 重度拥挤 | 是 | 753 | -70 |
误差的方差是: 70 × 70 + 70 × 70 = 9800
节假日的均值是:(375 + 542 + 437 )/ 3 = 451
| 天气类型 | 交通状态 | 工作日 | GAP数 | 误差 |
|---|
| 雷暴 | 轻度拥挤 | 否 | 375 | -76 |
| 晴 | 拥挤 | 否 | 542 | +91 |
| 雪 | 拥挤 | 否 | 437 | -14 |
误差的方差是: 76 × 76 + 91 × 91 + 14 × 14 = 14253
按照是否为工作日分裂之后的总误差是 9800 + 14253 = 24053
当然标准做法是计算所有的总误差,然后选取最小的总误差的特征作为分类特征
(如果在这里结束,则认为工作日的预测是823,节假日的预测是541当然这还没有完)
第一颗树:
工作日:+823
休息日:+451
| 天气类型 | 交通状态 | 工作日 | GAP数 | 误差 |
|---|
| 晴 | 拥挤 | 是 | 893 | +70 |
| 晴 | 重度拥挤 | 是 | 753 | -70 |
| 雷暴 | 轻度拥挤 | 否 | 375 | -76 |
| 晴 | 拥挤 | 否 | 542 | +91 |
| 雪 | 拥挤 | 否 | 437 | -14 |
第二颗树:
如果按照拥挤分类呢?
注意这里我们使用的输入值是误差!!
| 天气类型 | 交通状态 | 工作日误差 |
|---|
| 晴 | 拥挤 | +70 |
| 晴 | 拥挤 | +91 |
| 雪 | 拥挤 | -14 |
| 雷暴 | 轻度拥挤 | -76 |
| 晴 | 重度拥挤 | -70 |
首先计算均值:
轻度拥挤 : -76
重度拥挤 : -70
拥挤 : +49
(这些数字的意思是,如果你认为工作日的预测是823,节假日的预测是541,两者都需要根据拥挤程度根据上述值进行修正)
| 天气类型 | 交通状态 | 工作日误差 | 交通状态误差 |
|---|
| 晴 | 拥挤 | +70 | +21 |
| 晴 | 拥挤 | +91 | + 42 |
| 雪 | 拥挤 | -14 | - 63 |
| 雷暴 | 轻度拥挤 | -76 | 0 |
| 晴 | 重度拥挤 | -70 | 0 |
第三颗树:
| 天气类型 | 交通状态:拥挤 |
|---|
| 晴 | +21 |
| 晴 | + 42 |
| 雪 | - 63 |
晴天:+ 31
雪:- 63
在交通状态为拥堵的时候,如果是晴天,修正 31,雪:修正 -63
预测一下
工作日 +823
拥挤:+49
拥挤 且 雪天:-63
预测:809
C#代码
回归分类树节点
///
/// 回归分类树节点
///
class TreeNode
{
///
/// 节点属性名字
///
public string attrName { set; get; }
///
/// 节点索引标号
///
public int nodeIndex { set; get; }
///
/// 包含的叶子节点数
///
public int leafNum { set; get; }
///
/// 节点误差率
///
public double alpha { set; get; }
///
/// 父亲分类属性值
///
public string parentAttrValue { set; get; }
///
/// 孩子节点
///
public TreeNode[] childAttrNode { set; get; }
///
/// 数据记录索引
///
public List dataIndex { set; get; }
}
数据挖掘入门与实战
搜索添加微信公众号:datadw
教你机器学习,教你数据挖掘

长按图片,识别二维码,点关注
公众号: weic2c
据分析入门与实战

长按图片,识别二维码,点关注














