(
宝安区开学考
)
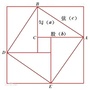
如图，在
钝
角
△ABC
中，
tan∠ABC=
,AC=10,BC=20,D
是
AC
的中点，延长
BE
至点
E
，满足
∠DCE=∠ABC
，则
CE=_______
方法一：过点
C
作
CG⊥BC
交
BA
延长线于点
G
，
设∠
ABC=
α
，则
tan
α
=
，得
CG=10
，
BG=10
，且有
CA=CG
，于是∠
CAG=
∠
G
，而
α
+
∠
G=90
°，∠
CAG+
∠
ACE=90
°，延长
CE
交
AG
于点
F
，则
CF
⊥
BG
，且
AF=2
，
CF=4
，
AB=6
，连接
DF
，则∠
DFC=
∠
DCF=
α
=
∠
FCG
，得
DF||CG
，在△
BGH
中，有
点评：此法主要是线段数据与正切值产生的联系而得,通过辅助线可得等腰三角形，利用特殊点可得平行线，利用比例得CE的长.
方法二：
12345
原理
作
CF
平分
∠ACB
，知
tanβ=1/3
,
而
tanα=1/2
,
得
α+β=45°
，即∠
CFG=45
°，同理得∠
FCG=45
°，
点评：
12345模型，初中平面几何不得不说，掌握好可以秒解很多题目
延长
CE
交
BA
延长线于点
G
，知
CG
⊥
BG
，
CG=4
，
AG=2
，
AB=6
,
过点
D
作
DH||BG,D
为
AC
的中点得
DH=
,
且
CH=GH,
而
DH
：
BG=1
：
4
，得
EH
：
GH=1
：
3
，得
CE
：
EG=3
：
4
，得
CE=
方法三：
平行构造相似
过点
D
作
DM||BC
交
CE
于点
M
由
∠CDM=∠ACB
，
∠DCM=∠ABC
得
△CDM~△BCA
，得
DM=5/2
，
CM=
，而
得
EC=
点评：方法三、方法四、方法五，有类似之处，都是利用相似+平行，双重比例求出线段长.
方法四：相似
过点
A
作
AG||BE,
得
E
为
GC
的中点，
FG:GE=FA:AB=1:3,
得
EF
：
EC=4
：
3
，得
EC=
方法五：平行
+
相似
过点
A
作
AN||CE
交
BD
于点
M
，交
BC
于点
N
，
易知△
CAN~
△
CBA
得
AN=3
，
CN=5
，
BN=15
，
MN
：
CE=BN
：
BC=3
：
4
，同时△
AMD
≌△
CED
，得
AM=EC
，故
AM
：
MN=4
：
3
，得
EC=AM
=
方法六：解三角形
(
可自行处理
)
