Evasion of tipping in complex systems through spatial pattern formation
期刊:
Science
DOI
:
10.1126/science.abj0359
日期:
2021
年
10
月
8
日
一作兼通讯:
Max Rietkerk
机构:
Utrecht University
,
Netherlands
写在前面
临界点(
tipping point
,也有称为转折点)是生态系统监测、预警等方面的一个重要概念。外源或内源扰动超过一定限度(
threshold
),可能会导致生态系统从一个平衡态跃变到另一个相对较次的平衡态,并且不易恢复。公众号此前多篇推文曾介绍过生态系统临界点的必要性和重要性。
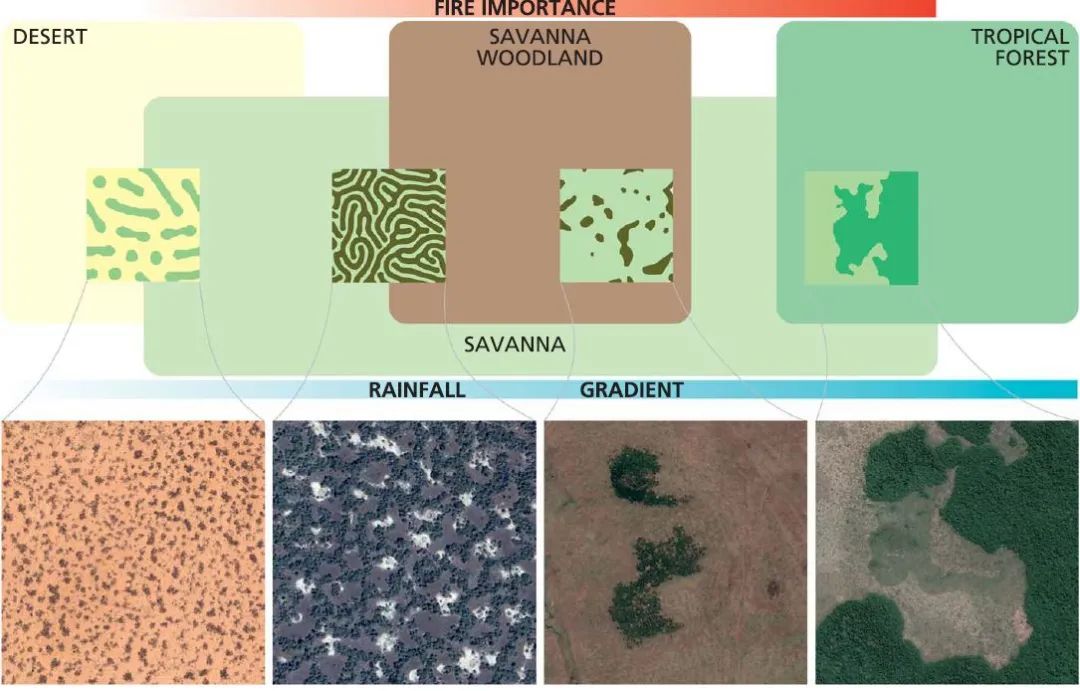
现在研究的一个重点就是,如何寻找系统跃变的早期预警信号。以空间尺度较大的生态系统(比如旱地和稀树草原系统)为例,已有研究认为,这些生态系统的临界转变往往伴随着规则的植被
空间自组织
格局的形成。即,随着环境条件的恶化,植被覆盖的均一性(
uniform coverage
)无法维持,并逐渐转变为具有一定规则的空间格局(
regular spatial patterns
)。本期推荐的综述文章则认为,这种
空间自组织
斑图的形成,未必是跃变的早期预警信号。相反地,由于生态系统异质性和多稳态的共存,这种空间自组织斑图的形成可能是生态系统弹性的表征,可以帮助生态系统规避临界点。
文章简介
当前的地球正处于所谓的人类世(
anthropocene
)。处于同一时期的人类,则不得不思考气候变化和土地利用变化等过程对地球及其相关生态系统的可能影响。临界转变(
critical transitions
)是理解上述内容的重要概念之一。在外力扰动下,系统可能被迫跃出原始平衡态的吸引域(
basin of attraction
),而转入一个相对较次的平衡态
——
这一转变即称为临界转变。基于此,目前研究的一个重点就是寻找生态系统状态跃变的早期预警信号(
early warning signals
)。基于空间自组织形成的“图灵斑图(
Turing patterns
)”是目前备受关注和认可的一个早期预警信号。
(长期以来,人们对生态系统
空间自组织(
spatial self-organization
)
斑图的认识主要是基于计算机和人工智能之父艾伦·图灵(
Alan Turing
)提出的尺度依赖性“活化子
-
抑制子
”
理论(也称为“图灵理论”)。“图灵理论
”
很好地描述了生态系统中种群出生、死亡、迁移等生态过程,并且用布朗运动近似描述了生物个体的运动行为特征。“图灵斑图”故此得名。)
然而随着研究和观测的发展,一些研究发现这种空间自组织未必是系统临界转变的早期预警信号。相反地,空间自组织协助生态系统规避临界点,从而使自身成为生态系统弹性的信号。这些研究主要是基于近期的空间模型数学分析和对真实生态系统的观测。这两种方法都揭示了生态系统的多稳态特征。即,在同一环境条件下,共存有多种不同的空间格局,其中每种格局都可以在较宽的条件变化幅度内稳定存在。结果就是,通过空间自组织,复杂生态系统的状态可以在临界点之外继续维持。
此外,具有临界性质的复杂系统在遇到扰动后,后续改变的发生未必会导致整个系统趋于临界。相反地,由于系统自身允许多个状态的共存(
coexistence states
,“共存态”),所谓的改变可能只发生在局部区域。通过这一替代途径,即使环境条件继续恶化,这些空间格局也可能在临界点之外继续维持。本研究将“图灵斑图”和“共存态”都视为空间自组织。通过多种多样的空间自组织途径来规避临界点,可能对很多的生态系统,包括地球本身,都具有重要意义。
为了更好地理解复杂生态系统如何通过空间自组织来规避临界点,本研究以稀树草原生态系统(
savanna ecosystems
)为例进行了详细说明。此外,本研究认为,通过更多的数学分析,应该可以获取生态系统和地球系统各组分规避临界点的通用条件。未来还需要分析,在何种情境下,小规模的“图灵斑图
”
可以生成、并聚集成大规模的局域性互作结构,从而协助复杂系统规避临界点。此外,还需要关注全球变化对“共存态”边界的影响,以及人为活动对空间域的限制作用和同质化过程的影响。
图表解读
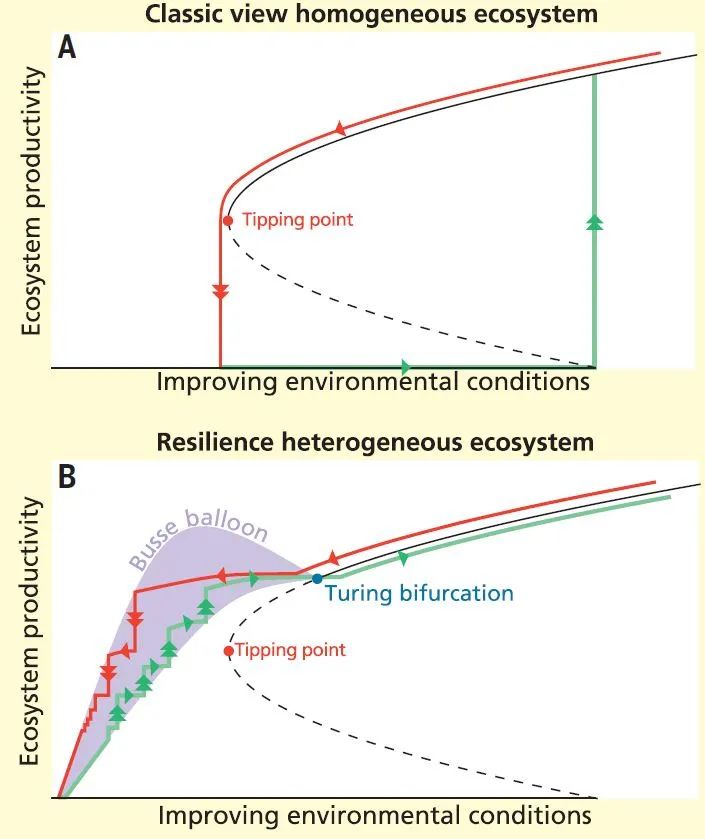
图
1.
均质与异质生态系统的弹性(
resilience
)。图中,实线表示稳定平衡,虚线表示不稳定平衡。双箭头表示生态系统的转变(转换),单箭头表示生态系统的微调。图中给出了生态系统退化(红色)与恢复(绿色)的典型轨迹,从中可以看出,具有异质性和空间自组织特征的生态系统,具有相对较窄小的迟滞圈(
hysteresis loop
)。(
A
)均质(
homogeneous
)生态系统的弹性。通常认为,随着环境条件的恶化,生态系统的状态或者生产力会发生小幅度的调整。当环境条件的改变越过临界点(
tippingpoint
,图中红色点),生态系统就会发生灾难性转变(
B-
临界点)。(
B
)异质(
heterogeneous
)生态系统的弹性。在多稳态生态系统中,图灵分岔点(
Turing bifurcation
,图中蓝色点)之外的任一环境条件,都会驱动系统进入多重稳定、空间自组织状态,即图中的紫色阴影区域(也称为
Busse balloon
)。此种情形下,生态系统中会发生很多的小转变(
smaller shifts
),而非临界转变(
critical transition
)。这些小转变对生态系统整体的功能和生产力的影响是比较小的。