基于深度学习的图像检索

算法与数学之美 · 公众号 · 算法 · 2017-03-20 22:04

正文

“

基于深度学习的图像检索：Deep Learning of Binary Hash Codes for Fast Image Retrieval

来源：知乎和傻牛一起闯天下

编辑：Gemini

Deep Learning of Binary Hash Codes for Fast Image Retrieval 这篇文章发表在2015CVPR workshop

文章链接：http://www.cv-foundation.org/openaccess/content_cvpr_workshops_2015/W03/papers/Lin_Deep_Learning_of_2015_CVPR_paper.pdf

代码链接：https://github.com/kevinlin311tw/caffe-cvprw15

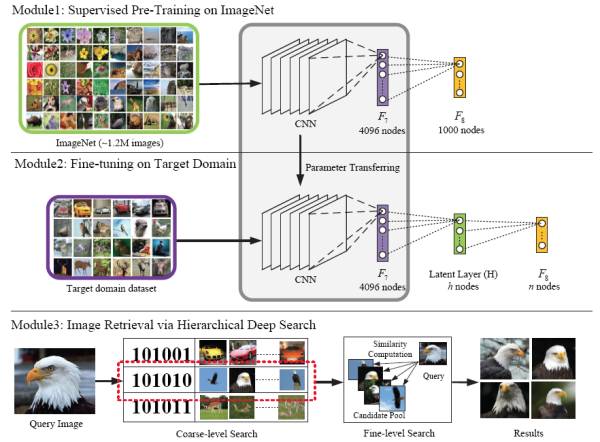
图一算法框架流程

这篇文章的想法很巧妙，在一个深层CNN的最后一个全连接层（fc8）和倒数第二个全连接层（fc7）之间加了一层全连接隐层，就是图一中绿色的latent layer （H）。这样一来，既可以得到深层的CNN特征，文中主要用的是fc7的特征，还可以得到二分的哈希编码，即来自H。这个隐层H不仅是对fc7的一个特征概括，而且是一个连接CNN网络的中层特征与高层特征的桥梁。

1. Domain Adaption

为了让一个网络能够对某一类物体高鲁棒，即target domain adaption，用一类主题目标数据集来整定(fine-tune)整个网络。fc8的节点数由目标类别数决定，H的节点数在文中有两种尝试：48和128。这两个层在fine-tune时，是随机初始化的，其中H的初始化参考了LSH[1]的方法，即通过随机映射来构造哈希位。通过这样训练，得到的网络能够产生对特定物体的描述子以及对应的哈希编码。

2. Image Retrieval

主要提出了一种从粗糙到细致的检索方案（coarse-to-fine）。H层首先被二值化：

粗糙检索是用H层的二分哈希码，相似性用hamming距离衡量。待检索图像设为I，将I和所有的图像的对应H层编码进行比对后，选择出hamming距离小于一个阈值的m个构成一个池，其中包含了这m个比较相似的图像。

细致检索则用到的是fc7层的特征，相似性用欧氏距离衡量。距离越小，则越相似。从粗糙检索得到的m个图像池中选出最相似的前k个图像作为最后的检索结果。每两张图128维的H层哈希码距离计算速度是0.113ms，4096维的fc7层特征的距离计算需要109.767ms，因此可见二值化哈希码检索的速度优势。

3. 实验结果

作者在MINIST，CIFAR-10，YAHOO-1M三个数据集上做了实验，并且在分类和检索上都做了实验，结果都很不错，特别是在CIFAR-10上图像检索的精度有30%的提升。

（1）MINIST

左边第一列是待检索图像，右边是48和128位H层节点分别得到的结果。可以看到检索出的数字都是正确的，并且在这个数据集上48位的效果更好，128位的太高，容易引起过拟合。

（2）CIFAR-10

在这个数据集上128位的H层节点比48位的效果更好，比如128检索出更多的马头，而48位的更多的全身的马。

（3）YAHOO-1M

作者在这个数据集上比较了只用fc7,只用H和同时用两者（粗糙到细致）的结果，实验结果表明是两者都用的效果更好。

可以看到如果只用alexnet而不进行fine-tune的话，检索出的结果精度很低。

4. 总结

这个方法整篇文章看下来给人的感觉比较工程，全篇讲理论和方法的部分很少，几乎没有什么数学公式，但是效果好，这个最重要。想法很简单，但是很巧妙，值得学习。代码已经开源，准备尝试。

[1] Gionis A, Indyk P, Motwani R. Similarity search in high dimensions via hashing[C]//VLDB. 1999, 99(6): 518-529.

往期经典文章回顾