文章链接:https://www.nature.com/articles/s41586-024-07156-y
文章摘要
材料中电子的谷自由度为实现节能信息存储提供了途径,并为量子信息处理带来了诱人的前景。当前利用谷偏振的挑战是需要单层结构或特定材料工程的对称条件、避免能量耗散的非谐振光学控制以及以光速切换谷偏振的能力。我们展示了使用块状 MoS2(一种在谷处没有贝里曲率的中心对称材料)对谷偏振的全光学和非谐振控制。我们的通用方法利用自旋角动量形状的三叶形光控制脉冲来切换材料的电子拓扑,并通过简单的相位旋转瞬时打破时间和空间反转对称性来诱导谷极化。我们通过非共线光学探针脉冲的二次谐波的瞬态生成来确认谷偏振,具体取决于三叶形相位旋转。研究表明,对谷自由度的直接光学控制并不限于单层结构。事实上,对于具有任意层数的系统和散装材料来说,这种控制是可能的。非谐振谷控制是通用的,并且在光速下,开启了设计在量子相干时间尺度上运行的高效多材料谷电子器件的可能性。
光波电子器件设想对用于太赫兹信息处理的材料中的载流子动力学进行子周期光学控制。除了速度之外,一个核心要求是编码信息以实现经典比特,其中材料固有的量子相关性为光波量子比特应用提供了一条途径。这种诱人的前景是与过渡金属二硫属化物(TMDC)半导体中电子带中的局部极值相关的谷赝自旋 。在单层形式中, K谷和K'谷分别用间隙谐振圆偏振光处理。光谷选择规则源自能带的轨道特征及其贝里曲率 。在块状TMDC中,这种光谷选择是不可行的,因此存在多种努力,致力于通过操纵介电环境来克服单层材料施加的限制,例如,通过应变工程、通过不同的堆叠配置、通过偏置层,或者通过使用层间激子。然而,实现光波谷电子学的重大障碍是(1)间隙共振激发,导致特定材料的谷切换速率和光学设置;(2)需要突破材料工程的反演对称性。更糟糕的是,大多数具有有趣量子特性的单层材料在质量、尺寸或环境稳定性方面都受到严重限制。与材料无关的光学控制方案将允许利用材料或材料组合来呈现否则无法获得的特定属性。
万能谷控制机制
在这里,我们将展示如图1a所示的强光学和非共振三叶形场提供了用于光学切换和控制块体六边形材料中的谷偏振的通用且与材料无关的手段。虽然参考已经暗示了这种可能性,但仍然利用了单层的固有空间反演对称性破缺,在这里我们展示了具有三叶形自旋角动量整形的非共振强光场打破了时间和空间反演对称性。三叶形控制场是双圆的,但两个场分量具有相反的旋向性,并且一个分量是另一个分量的二次谐波;参见图2中的插图。三叶形图案是六角形TMDC特有的,因为它的对称性与六角形材料的三角形子晶格相匹配,而六角形材料是三重对称的。
图1显示了应用强三叶形场的双层MoS2 (六方2H相,空间群194)的时间依赖性第一原理模拟的结果(图1a和方法)。图1b显示了第一个布里渊区中所有导带上的电子密度之和。尽管 A 层和 B 层之间旋转 180°,但 k 空间投影电子密度的颜色代码清楚地显示了谷极化。在这种情况下,谷偏振的机制与材料本征光谷选择规则所实现的机制根本不同。相反,所示的谷极化是由于对称选择规则而产生的。一方面,由于三叶形控制场和层子晶格之间的匹配对称性,复合激光修饰晶体中的空间反演对称性被打破。另一方面,三叶形控制场引起复杂的第二邻域跳跃
16(图1c),类似于Haldane拓扑模型中的情况,它打破了时间反转对称性并提升了谷简并性。虽然从理论上预测了后一种效应是针对破碎的反转对称单层结构的,但令我们惊讶的是,我们在图1b中看到了类似的效应,即使在中心对称双层情况下也是如此。为了说明物理机制,我们用图1d中修饰的带隙石墨烯系统的有效能带结构来补充数值模拟。我们使用实验的激光参数和无场 MoS2分析计算了激光修改的跳频;有关详细信息,请参阅方法和补充信息。图中可见的是三叶控制场旋转60°时K点和K′点之间的最小间隙切换。对于 30° 旋转(图1c和图1d,中间),三叶草场的方向对两个山谷的影响相同;也就是说,引起的第二邻居跳跃是真实的。
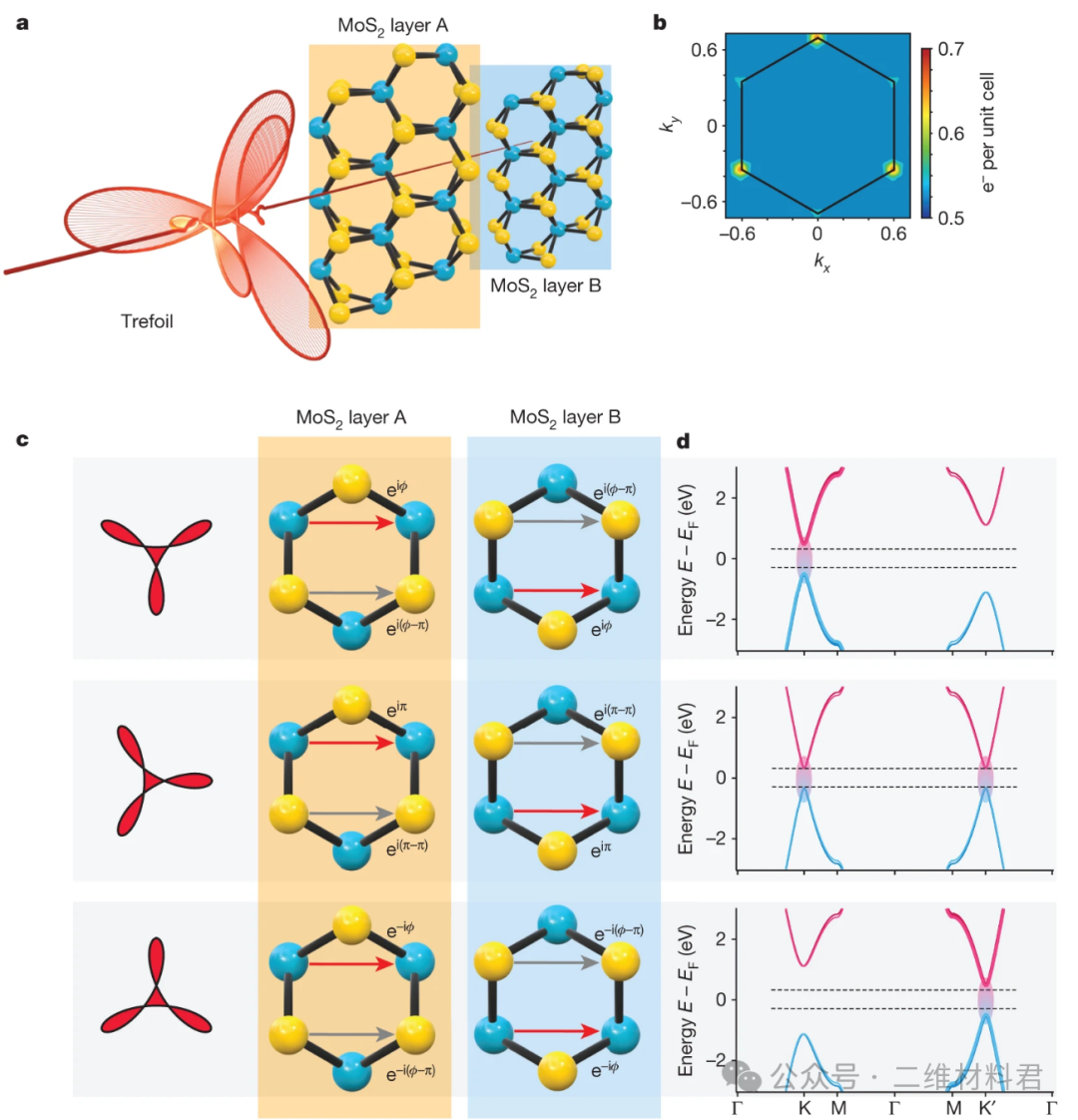
图 1:具有强三叶形场的块状 MoS2中的谷极化。a ,概念草图,显示三叶草场以及块体 2H-MoS2的 A 和 B 交替层。b,根据第一原理计算得出的谷极化第一布里渊池中的电子密度。c,不同原子成分之间的强场感应耦合以及特定三叶形方向的交替 A 层和 B 层。d,能带结构的相关变化。顶部和底部,K 和 K′ 处的谷极化;中、谷退化。
非谐振光控制
在实验中,我们通过将频率为ω 的圆偏振场与其圆偏振二次谐波相结合,在双色马赫-曾德干涉仪(图2)中合成来自中红外光学参量啁啾脉冲放大器系统30 的三叶形场。 2 ω沿相反方向旋转。该激光系统以 160 kHz 的重复频率提供载波包络相位稳定的 3.2 µm、103 fs 脉冲。该输出的一小部分能量进入马赫-曾德干涉仪,在其中一个臂中产生二次谐波。两个臂均包含半波片、偏振器和四分之一波片,以调整基波 ( ω ) 和二次谐波 (2 ω ) 的相对场振幅和偏振状态。对于相反的螺旋度场,合适的相位延迟和 3:2 ( ω : 2 ω ) 的幅度比会导致在两个臂相干组合时生成三叶形场。测得的场振幅为0.032±0.004V Å -1。通过在ω和 2 ω处的光场之间插入相位延迟的楔形调整,可以在子激光周期时间尺度上控制方向。
第一步,我们微调马赫-曾德干涉仪的参数并确认三叶形场的产生。我们通过手性高次谐波光谱在块状 MoS 2的独立式 10.7 ± 0.2 µm 晶体样品上通过检查生成的谐波的对称性来实现这一点作为三叶形场方向的函数并将其与其双圆分量进行比较。图2b显示了样品的显微镜图像。图2b左下角样品的轻微扭曲揭示了晶体取向,从而允许相对于布里渊区调整泵浦和探测场方向。图2c显示了高次谐波光谱测量的结果:双圆分量的光谱,即3.2 µm处的右手圆场(红色填充曲线)、1.6 µm处的左手圆场(蓝色填充曲线)和 360° 旋转集成三叶形控制区域(黑色曲线)。正如中心对称块体 2H-MoS 2所预期的那样,右旋圆形 3.2 µm 场仅产生奇次谐波 H5 和 H7 。类似地,左手圆极化二次谐波场仅显示其基波场的三次谐波 H6。与单个场的情况形成鲜明对比的是,双色三叶形控制场产生偶次谐波阶次。 H8 次谐波最强,比本底噪声高 2.5 dB。奇次谐波 H5 和 H7 平均增加 4.6 倍,而 H6 则被抑制 4.3 倍。 H6 显着不同的行为是空间反演对称性破缺的结果。由此产生的C 3对称性导致 高次谐波产生的H(3 N ± 1)选择规则,其中H(3 N )阶被抑制( N是正整数)。在 H9 的情况下,非零信号归因于对较高非微扰谐波的抑制减少,正如我们在扩展数据图2中对可比三叶形场的模拟中观察到的那样。在使用设置中的光学传输函数进行校正后,我们的模型很好地再现了测量的高次谐波光谱,尤其是谐波次数的相对强度。图2d进一步证实了泵的三叶形特性。颜色图显示了谐波如何呈现六重对称性作为三叶形场方向的函数,从而确认了材料 2H 相的纯度。
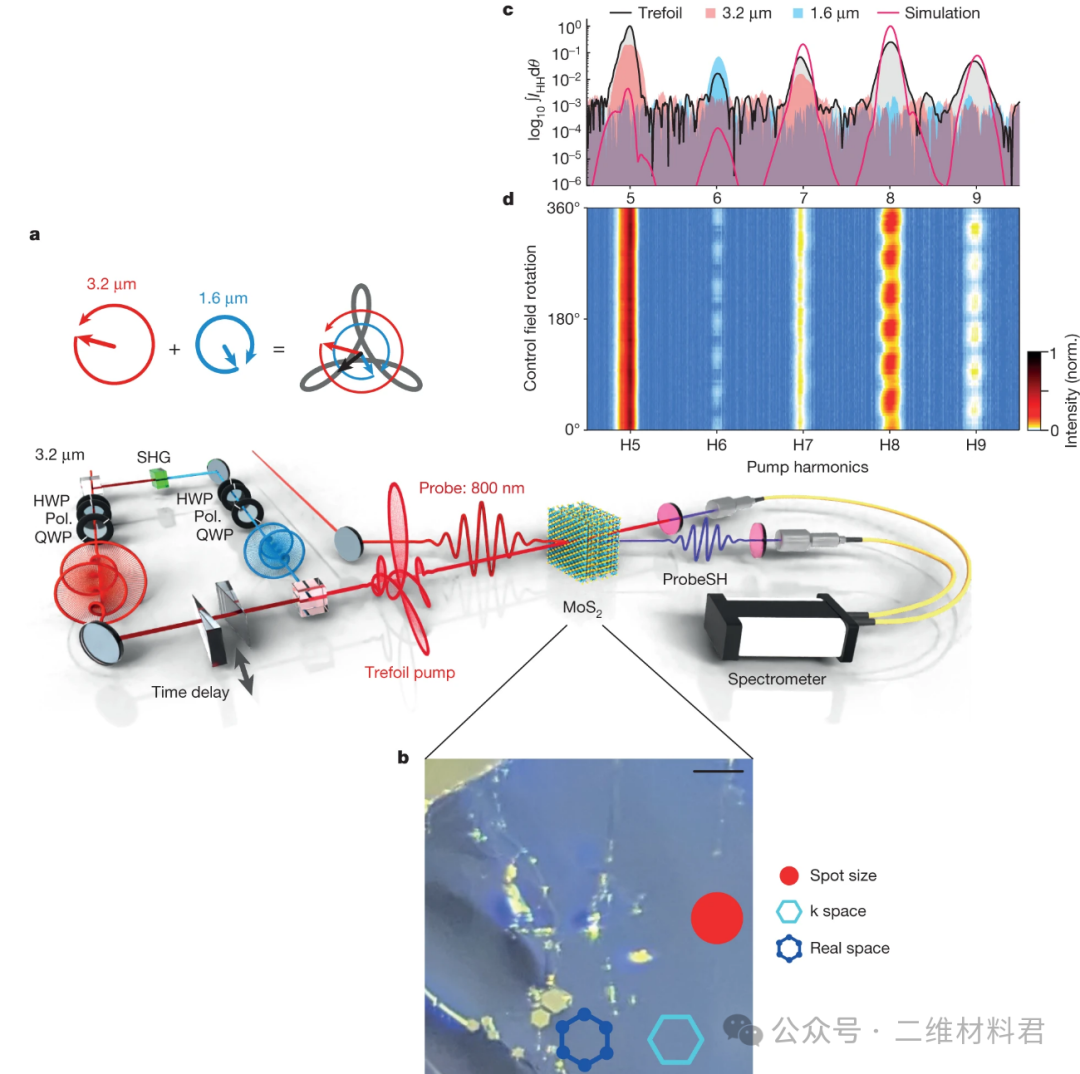
图 2:用于散装 MoS2谷值控制的泵浦-探针设置。a,在 Mach-Zehnder 装置中利用 3.2 和 1.6 µm 的双圆脉冲合成三叶草。 103 fs 半高全宽输入脉冲 3.2 µm 在 Mach-Zehnder 臂之间分配;一部分被倍频以产生二次谐波。两个波长处的相对场振幅可通过每个臂中的半波片 (HWP) 和偏振器 (Pol.) 独立调节。调整四分之一波片 (QWP) 以产生相反旋向的圆偏振。圆形部件在分束器处相干地重新组合,产生三叶形结构。马赫-曾德尔臂之一中的薄楔子可以调整相位,从而导致三叶形结构旋转。b ,MoS2独立样品的显微镜图像。缺陷(左下)可以直接识别晶体方向。样品的原始区域用于实验;指示光斑尺寸(红色)。 800 nm 处的探头是线性偏振的,并以s偏振以 30° 角撞击样品。探头和三叶草泵均被检测并进行光谱解析。c,各个圆形分量和角积分三叶形的谐波。d,三叶谐波作为旋转的函数。比例尺,100 μm;规范,规范化。
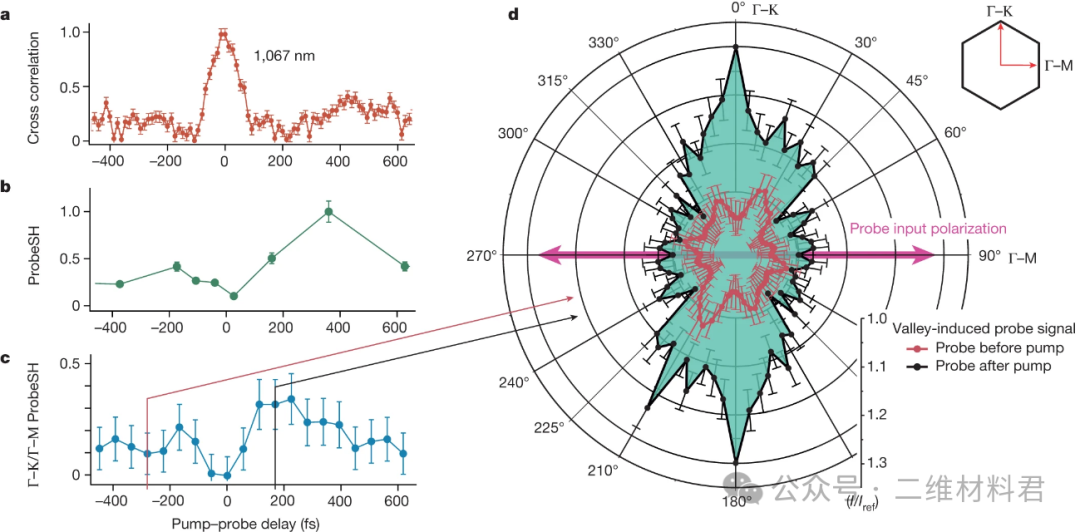
确认了三叶形场的产生后,我们现在研究其在诱导谷极化和控制块状 MoS2方面的功效。我们使用场强为 0.012 ± 0.002 V Å -1的附加弱 800 nm 探针场来检查电子结构的变化以及时空反演对称性的破坏作为三叶形场方向的函数。 800 nm 探测场是线性偏振的,并在s偏振中非共线地询问材料,从而提供无背景测量。在没有三叶形场的情况下,由于多层 2H-MoS2的中心对称性质,从体相中观察不到探针的二次谐波产生(SHG)。由三叶形控制场引起的谷极化引起的对称性变化记录为探头二次谐波 (ProbeSH)。图3显示了三叶草场和探针之间泵浦探针延迟扫描的结果。
三叶泵浦和 800 nm 探测光束的同步光谱测量揭示了泵浦-探测延迟为零时的强参数相互作用。避免这样的背景是非共线探针几何形状的原因。图3a显示了三叶草的 3.2 µm 组件与 1,067 nm 处的 800 nm 探头之间的互相关性,这提供了最大延迟时间“零”。为了测量 ProbeSH,我们记录了 400 nm 处 60° 调制探针信号的功率谱密度(参见方法和扩展数据图3),如图3b所示。我们通过在整个周期内每个泵浦-探测延迟步骤旋转三叶形场来获得这条曲线。对于时延“零”,我们观察到由于强参数相互作用消耗了 800 nm 处的探针基波,ProbeSH 显着减小。因此,这也导致图3b、c中的信号大幅减少。延迟扫描显示,ProbeSH 在三叶草泵之后约 360 fs 达到最大。我们注意到这种延迟与理论预测一致。 ProbeSH 本身的出现就是反演对称性破缺的明显标志,因为如果没有来自体相的三叶形场,它就不会出现。然而,它的起源可以有两个方面:由于打破谷简并性和三叶向量势对谷势的重塑。我们现在将理清这些贡献。