博弈类问题的套路都差不多,下文举例讲解,其核心思路是在二维 dp 的基础上使用元组分别存储两个人的博弈结果。
掌握了这个技巧以后,别人再问你什么俩海盗分宝石,俩人拿硬币的问题,你就告诉别人:
我懒得想,直接给你写个算法算一下得了。
举个例子:
你和你的朋友面前有一排石头堆,用一个数组 piles 表示,piles[i] 表示第 i 堆石子有多少个。
你们轮流拿石头,一次拿一堆,但是只能拿走最左边或者最右边的石头堆。
所有石头被拿完后,谁拥有的石头多,谁获胜。
石头的堆数可以是任意正整数,石头的总数也可以是任意正整数,这样就能打破先手必胜的局面了。
比如有三堆石头
piles = [1,100,3]
,先手不管拿 1 还是 3,能够决定胜负的 100 都会被后手拿走,后手会获胜。
假设两人都很聪明
,请你设计一个算法,返回先手和后手的最后得分(石头总数)之差。
比如上面那个例子,先手能获得 4 分,后手会获得 100 分,你的算法应该返回 -96。
这样推广之后,这个问题算是一道
Hard
的动态规划问题了。
博弈问题的难点在于,两个人要轮流进行选择,而且都贼精明,应该如何编程表示这个过程呢?
一、定义 dp 数组的含义
定义 dp 数组的含义是很有技术含量的,同一问题可能有多种定义方法,不同的定义会引出不同的状态转移方程,不过只要逻辑没有问题,最终都能得到相同的答案。
我建议不要迷恋那些看起来很牛逼,代码很短小的奇技淫巧,最好是稳一点,采取可解释性最好,最容易推广的设计思路。
本文就给出一种博弈问题的通用设计框架。
介绍 dp 数组的含义之前,我们先看一下 dp 数组最终的样子:
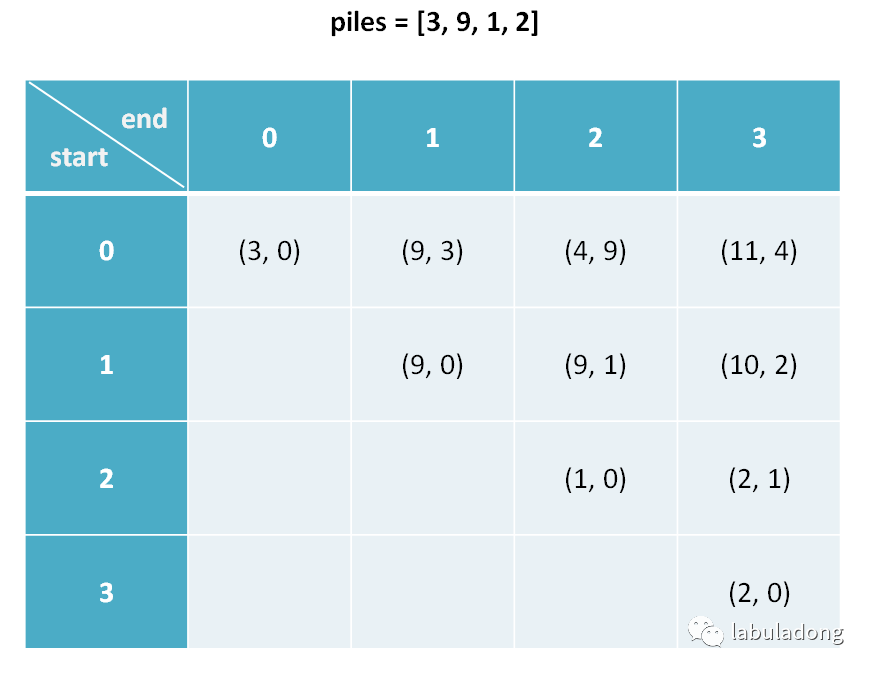
下文讲解时,认为元组是包含 first 和 second 属性的一个类,而且为了节省篇幅,将这两个属性简写为 fir 和 sec。
比如按上图的数据,我们说
dp[1][3].fir = 10
,
dp[0][1].sec = 3
。
先回答几个读者可能提出的问题:
这个二维 dp table 中存储的是元组,怎么编程表示呢?
这个 dp table 有一半根本没用上,怎么优化?
很简单,都不要管,先把解题的思路想明白了再谈也不迟。
以下是对 dp 数组含义的解释:

我们想求的答案是先手和后手最终分数之差,按照这个定义也就是
dp
[0][
n
−1].
f
i
r
−
dp
[0][
n
−1].
sec
二、状态转移方程
写状态转移方程很简单,首先要找到所有「状态」和每个状态可以做的「选择」,然后择优。
根据前面对 dp 数组的定义,
状态显然有三个:
开始的索引 i,结束的索引 j,当前轮到的人。
dp[i][j][fir or sec]
其中:
0 <= i i <= j
对于这个问题的每个状态,可以做的
选择有两个:
选择最左边的那堆石头,或者选择最右边的那堆石头。
我们可以这样穷举所有状态:

上面的伪码是动态规划的一个大致的框架,股票系列问题中也有类似的伪码。
这道题的难点在于,两人是交替进行选择的,也就是说先手的选择会对后手有影响,这怎么表达出来呢?
根据我们对 dp 数组的定义,很容易解决这个难点,
写出状态转移方程:

根据 dp 数组的定义,我们也可以找出
base case
,也就是最简单的情况:

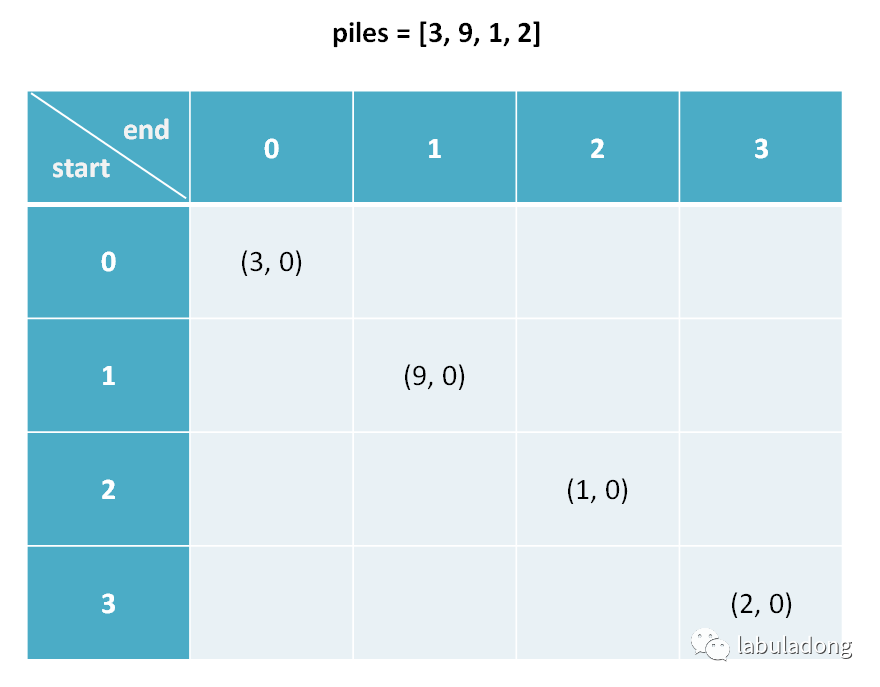
这里需要注意一点,我们发现 base case 是斜着的,而且我们推算 dp[i][j] 时需要用到 dp[i+1][j] 和 dp[i][j-1]:
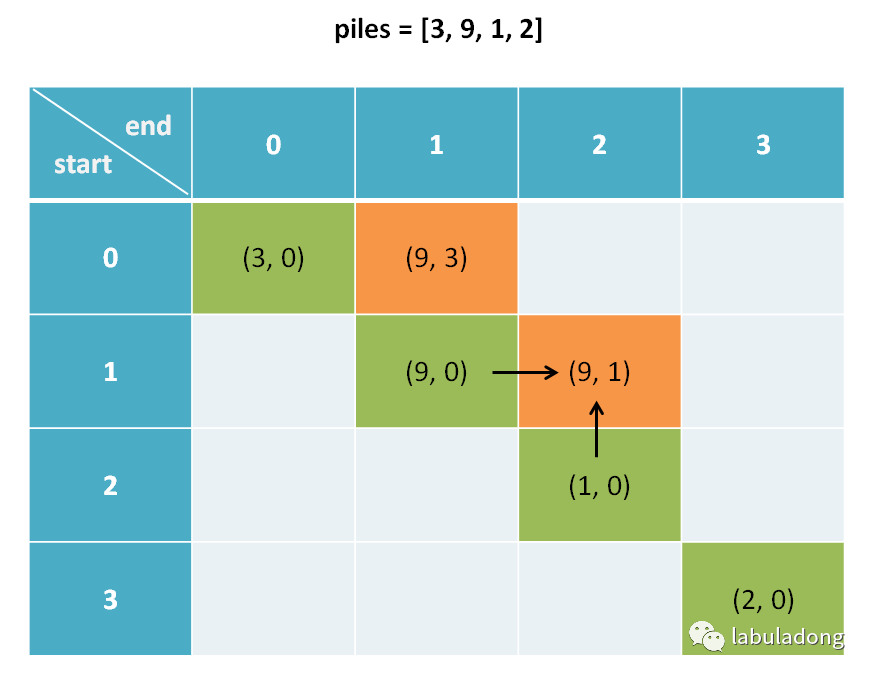
所以说算法不能简单的一行一行遍历 dp 数组,
而要斜着遍历数组:
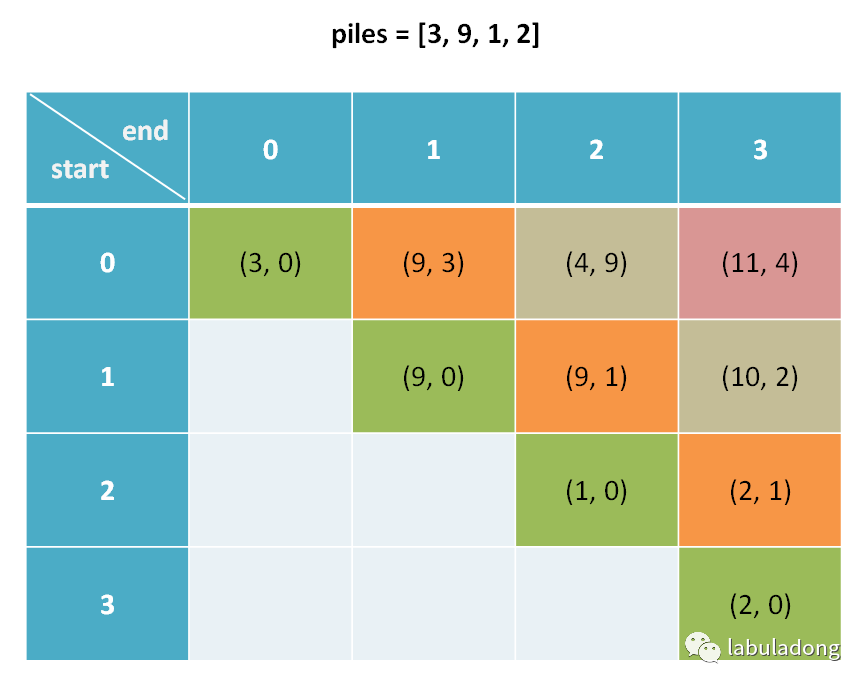
说实话,斜着遍历二维数组说起来容易,你还真不一定能想出来怎么实现,不信你思考一下?
这么巧妙的状态转移方程都列出来了,要是不会写代码实现,那真的很尴尬了。
三、代码实现
如何实现这个 fir 和 sec 元组呢,你可以用 python,自带元组类型;
或者使用 C++ 的 pair 容器;
或者用一个三维数组
dp[n][n][2]
,最后一个维度就相当于元组;
或者我们自己写一个 Pair 类:
class Pair {
int fir, sec;
Pair(int fir, int sec) {
this.fir = fir;
this.sec = sec;
}
}
然后直接把我们的状态转移方程翻译成代码即可,可以注意一下斜着遍历数组的技巧:

动态规划解法,如果没有状态转移方程指导,绝对是一头雾水,但是根据前面的详细解释,读者应该可以清晰理解这一大段代码的含义。
而且,注意到计算
dp[i][j]
只依赖其左边和下边的元素,所以说肯定有优化空间,转换成一维 dp,想象一下把二维平面压扁,也就是投影到一维。
但是,一维 dp 比较复杂,可解释性很差,大家就不必浪费这个时间去理解了。
四、最后总结











