基础准备
前面详细介绍了对数线性模型的理论基础以及SPSS软件关于对数线性模型的菜单设置:
今天将推送SPSS关于对数线性模型的使用方法。先用【选择模型】菜单对多变量的主效应和交互效应项进行筛选,将对频数分布有显著影响的主效应项和交互作用项确定下来,然后再用【常规】菜单对筛选出来的主效应和交互效应建立对数线性模型。
饱和模型和非饱和模型
先解释下饱和模型和非饱和模型的区别与联系。饱和模型就是在对数线性模型中考虑了所有分类变量的主效应和交互效应,而非饱和模型则是将某些无统计意义的交互项从饱和模型中删除掉得到的新模型。
例如,研究性别、人种和血型的相关关系。如果是饱和模型,包括三个主效应:性别、人种和血型对频数分布的作用;交互效应:性别*人种、性别*血型、人种*血型、性别*人种*血型。如果通过主效应项和交互效应项的筛选后,发现某些效应项是无统计学意义的,那么将这些效应项剔出饱和模型,得到的新模型就是非饱和模型。
对数线性模型的饱和模型,拟合的结果是完美匹配的,就是实际频数和理论频数完全相等,拟合优度的卡方值(实际频数与理论频数的差异)等于0,这是因为交叉单元格的每个单元格内的频数都可以被完全的分解和效应解释,可以想象一下交叉单元格,每个单元格内的频数都可以划归为分类变量的某一个水平作用及几个水平的交互作用。
【模型选择】和【常规】
【模型选择】菜单做的是分层对数线性模型,而【常规】菜单做的是一般对数线性模型。一般对数线性模型可以对每个分类变量的每个水平及所有水平的交互效应给出详细的信息,因此一般对数线性模型要求研究者已经有一定的思路和线索,或者只对某些特定效应感兴趣,即已经有关于非饱和模型的设想,通过一般对数线性模型来验证模型设想。如果在研究之前,并不知道分类变量之间可能存在的关系,没有明确的模型设想,那么分层对数线性模型比较适宜,它可以帮助分析者筛选出有统计意义的效应项,帮助分析者建立非饱和模型,这就极大减小了分析工作量。
分层对数线性模型的分析过程主要是寻找符合实测频数分布的适当模型。适当模型不仅代表模型成立,而且要求模型尽量简单,将没有意义的交互作用删除,这样的模型才有分析效果。对数线性模型的模型选择过程包括以下情况:
-
首先建立饱和模型,然后采用向后去除的办法,逐步从模型中剔除无统计学意义的效应。剔除的判断标准就是检查剔除后模型与饱和模型的拟合优度差异,如果拟合优度变化很小,那么就剔除该效应项。
-
首先建立只包含主效应的模型,然后逐步检查交互项加入该模型后,该模型的拟合优度变化是否有差异,如果拟合优度有差异,那么就表示交互效应对模型有贡献,将交互项留在模型中,反之,如果拟合优度变化没有差异,那么交互效应就没有必要加入模型。
需要注意,无论采用哪种模型建立的策略,都要遵循以下原则:如果低阶的效应不存在,那么包含该低阶交互效应项的其他高阶交互效应也将不存在。反之,高阶交互效应有统计学意义,即使低阶效应项无统计学意义,也应将其保留在模型中。例如,研究性别、人种和血型的相关关系,如果性别的主效应项没有意义,那么包含性别变量的所有交互效应都没有意义;如果性别*人种交互效应有统计意义,那么性别和人种两个变量的主效应有统计学意义。
案例分析
生活是数据分析的来源,这也是草堂君做生活统计学公众号的初衷,因此草堂君在介绍每种数据分析方法时,都会基于案例数据的分析背景介绍一些生活常识。真所谓生活中来、生活中去,希望大家在学习的同时拓展大家的知识面。喜欢就下方点个赞,留个言吧!
今天案例的背景是子宫后倾,那就先聊聊什么是子宫后倾以及子宫后倾的危害。子宫后倾又称为子宫后位,是比较常见的临床现象。如下图所示:
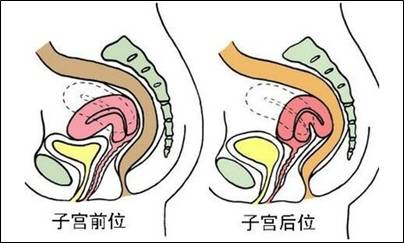
如果子宫纵轴不变,整个子宫向后方倾倒,容易使子宫颈呈上翘状态,即子宫后倾。通常来说,子宫后倾被大家熟知的危害是让女子不易受孕,原因是不易浸泡在精液池中而影响受孕。绝大多数的子宫后倾都能够通过特殊的体位顺利怀孕,只有少数较严重的患者需要接受外科治疗。
某妇幼保健院有个课题,研究子宫后倾的形成因素。通过前期的初步调查,发现子宫后倾与工作姿势和有无生育史有一定相关性。医院从数据库中随机抽取了370名劳动强度和年龄相仿的女职工,并记录她们工作姿势、有无生育史和子宫后倾情况的频数数据,形成下面的SPSS数据:
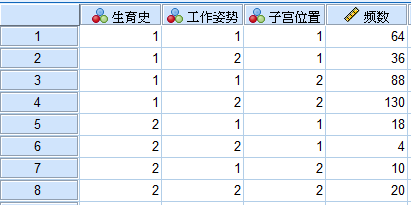
(例题数据文件已经上传到QQ群中,需要的朋友可以前往下载)
分析思路
有无生育史、工作姿势和子宫位置都是分类变量,研究它们之间的相关关系,可以多次使用卡方检验分析,也能通过对数线性模型进行研究。在做对数线性模型分析时,需要首先对数据进行加权处理,原理和操作步骤可以回归这篇推送:
SPSS分析技术:加权个案;让频数记录数据也能用SPSS做列联表分析
。
因为涉及到三个分类变量,因此首先使用【模型选择】菜单做分层对数线性模型分析,然后再用【常用】菜单的一般对数线性模型建立模型,给出结论。
分析步骤
1、选择菜单【分析】-【对数线性】-【选择模型】。将生育史、工作姿势和子宫位置三个分类变量选入因子中,然后点击【定义范围】,因为三个分类变量都是二分类变量,所以最小值填写1,最大值填写2(根据两个类别的数值定义填写)。模型构建使用上面提到的向后去除法,最大步骤数和除去概率保持默认数值即可。
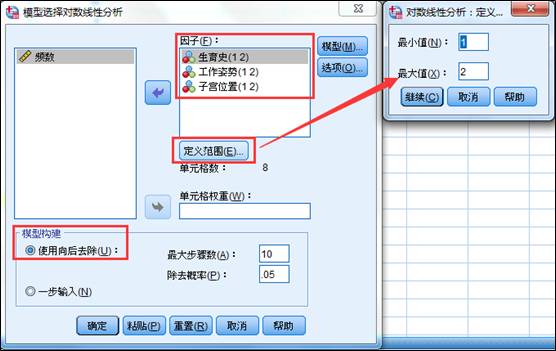
2、点击【确定】,输出结果。
结果解释
1、初始对数线性模型的拟合优度。由于我们没有对模型进行定制,所以初始模型是饱和模型,因此拟合优度检验的卡方值为0。
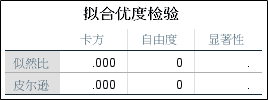
2、K向效应和更高阶效应。下方表格内容显示的是模型中K维交互作用和K维以上交互作用是否有统计学意义,方法是似然比卡方和皮尔逊卡方,无论哪种检验均显示三维交互作用无统计学意义,而二维交互和一维交互(主效应)有统计学意义。
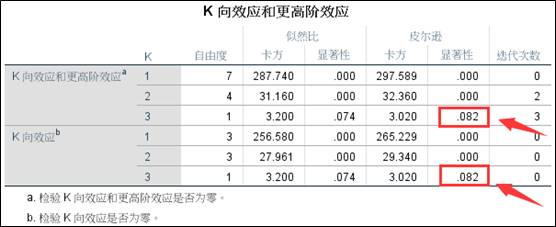
3、分层对数线性模型筛选过程。从结果可知,及鞥过5步以后,最后剩下的效应项有工作位置*子宫位置的二维交互项和生育史主效应,此外当然也包括工作姿势和子宫位置的主效应,原因在上面介绍向后剔除内容是介绍过。因此最后得到的简化线性对数模型效应项包括三个主效应:生育史、工作姿势和子宫位置;一个二阶交互项:工作姿势*子宫位置。
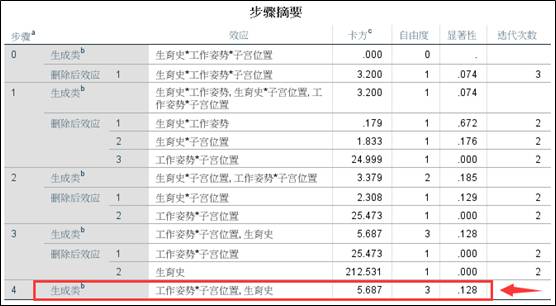
筛选过程的解释如下:
-
第0步:删除三阶交互效应项后,模型的拟合优度的显著性为0.074,大于0.05,说明删除后的模型与饱和模型没有显著性差异,因此可以将三阶交互效应项删除。
-
第1步:剩下的最高阶交互效应是三个二阶交互效应项,可以发现,删除生育史*工作姿势和生育史*子宫位置后,模型卡方检验显著性大于0.05,因此这两项都能够删除。
-
第2步和第3步:逐步删除两个没有统计学意义的二阶交互项。
-
第4步:得到最终的简化不饱和模型,一个二阶交互项:工作姿势*子宫位置,三个主效应项:工作姿势、子宫位置和生育史。
接下来,使用【常规】菜单,进行一般对数线性模型分析。选择菜单【分析】-【对数线性】-【常规】,将生育史、工作姿势和子宫位置选入因子框内;然后选择单元格计数分布为多项分布。
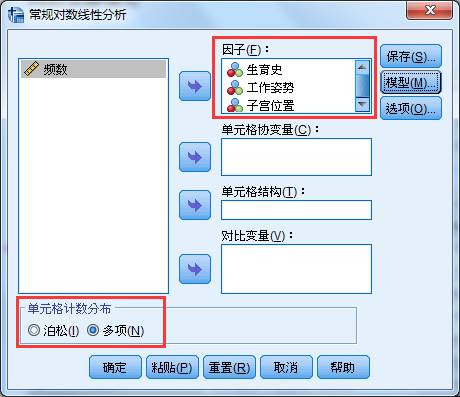
点击【模型】按钮;选择定制模型,然后按照上面分析结果,将三个主效应项和一个二阶交互作用项选中,建立模型。
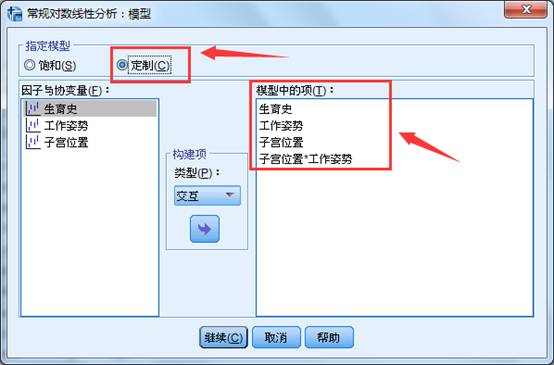
点击【确定】,输出结果。
结果解释
1、实测频数和模型拟合频数的差异表格。该表格显示实测频数和通过模型拟合得到的期望频数,并计算它们之间的差异。
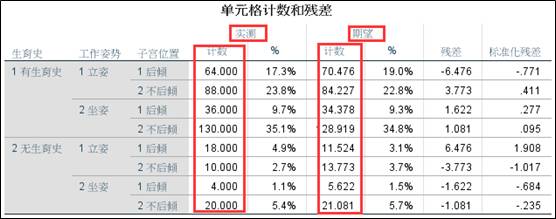
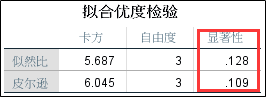
2、不饱和模型的拟合优度检验;结果显示,建立的不饱和模型的两种拟合优度检验结果都大于0.05,说明与饱和模型的差异不显著,也就是说建立的模型是有效的。
3、对数线性模型结果。
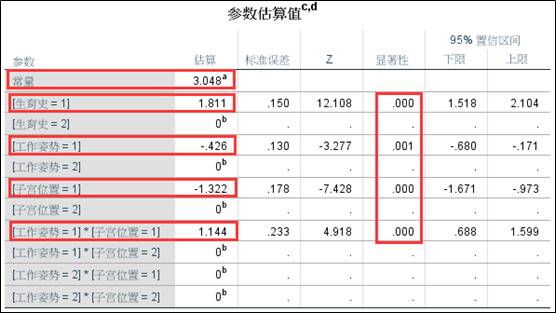
上表是对数线性模型的各参数估计值。模型共有11个参数,但真正进入模型的参数只有5个,这是因为三个分类变量(主效应项)的其中一个分类水平作为参考水平,系数为0,因此最终的系数包括1个常数项,3个主效应项,1个二阶交互项。如果显著性小于0.05,那么说明回归系数所对应的效应项有统计学意义。从结果可知,所有系数都有统计学意义。
根据案例的研究目的,关心的是工作姿势*子宫位置、生育史*子宫位置和生育史*工作姿势*子宫位置这三个交互效应的显著性结果,通过【选择模型】,剔除了没有统计学意义的生育史*子宫位置、生育史*工作姿势*子宫位置这两个交互效应项。剩下的工作姿势和子宫位置通过一般对数线性模型分析,发现其回归系数为1.144,显著性小于0.05,说明工作姿势确实和子宫位置有相关关系。
这里的回归系数的意义是单元格频数的自然对数转换值。这里距离说明,常数项为3.048,exp(3.048)=21.081,也就是三个分类变量作为参考水平的对应单元格的频数,如下图所示。而交互效应项的系数1.144,exp(1.144)=1.139,代表的含义为期望频数70.476/84.227除以34.378/128.919的值,也就是相对危险系数OR。其它的系数大家可以自己进行计算验证。
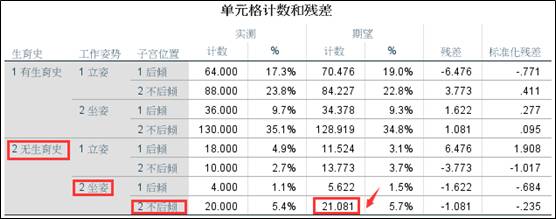
所有例题的数据文件都会上传到QQ群中,需要对照练习的朋友可以前往下载,QQ群号见下方温馨提示。
生活统计学不仅有各种数据分析方法,更有容易被大家忽视的生活常识。

















