智商低下
人生开挂
今天，小天情绪十分低落
，完全找不到工作状态，还差点哭出声。。。
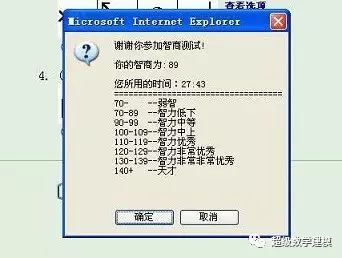
原来，是昨天有一好友发了个智商测试的链接过来，小天也对自己的智商比较好奇（自我感觉良好），于是便花了半个小时完成了测试，结果。。。
89∈智商低下！
这让小天感到十分慌张，于是便求救“万能”的超模君（想要得到超模君的肯定）：“你看我像智商低下的人吗？”
超模君第一反应就是“像啊”，不过看着小天有点“怀疑人生”的眼神，于是便不开玩笑了，安慰道：“才智商低下，又不是弱智。而且这些智商测试很多都是不准的啦，有位数学巨人也曾被测试为智商低下呢。”
小天惊喜万分：“真的吗？！”
超模君：“我什么时候骗过你
。。。”
事实上，早在1905年，法国著名的心理学家比奈和教育家西蒙设计出一种测量智商的量表，因准确率高而风靡全球。谁知突然间被砸了招牌，因为经这个表测验，被判定为“笨人”的群体中，居然有庞加莱，而庞加莱就是那位被公认为世界最后的数学百科全书的数学大师。
1854年4月，庞加莱降生在法国南锡城，从小就表现出极高的智力，有点小害羞，是个招人喜爱的孩子。然而上天却没有眷顾他，自幼患有的运动神经系统疾病，加上5岁时患上的白喉病，让他迅速成为了一个体弱多病、词不达意的人。
1862年，庞加莱开始了他很期待的校园生涯，可是年幼的他很快就发现不对劲了。当年的白喉病让视力受到损伤的庞加莱在上课时压根就看不清黑板的内容，实在没办法的他唯有靠听和记忆来进行学习。
年轻时还是挺帅的嘛
也许因为这样，他的大脑变得出奇的发达，还能过目不忘，甚至能够无需纸笔直接在脑海进行复杂的运算，写作也能一次成型。
（
原来过目不忘也能后天养成）
庞加莱到底是不是数学神童就不知道了，最起码不是笨人。因为直到15岁他才第一次表现出对数学的兴趣，并很快就展现出非凡的数学天赋，以至于被称为“数学魔怪”。
1873年，庞加莱参加法国综合工科大学的入学考试。据说，当时为了测试他的才能特意延长考试时间，让他解答考官们精心设计的“漂亮问题”，结果庞加莱嗖嗖地就答完了，差点把主考官们吓出心脏病来。因此在他的绘画考试和几何作图都得了零分的情况下，他还是拿到了头名进入学校。
求主考官心理阴影面积
进入大学后，庞加莱开启了他勤勤恳恳的数学研究事业。
庞加莱在高斯对椭圆函数研究的基础上进一步推广椭圆函数理论，让他开始赢得国际声誉。紧接着，他在复变函数理论领域开创了单复变自守函数理论，还引入了一种叫自守函数的特殊函数。
所谓自守函数就是在某些变换群的作用下不变的函数，是椭圆函数、双曲函数、三角函数的推广。
庞加莱将复变函数推广到多变量函数，建立了研究多变量复变函数理论的基本方法。就这样，庞加莱一点一点地完善单复变自守函数理论，使得后人基本没有插足的余地。（真羡慕庞加莱与单复变自守函数理论可以长长久久地厮守着）
庞加莱可能觉得单复变自守函数理论已经没有可成长的空间了，便噼里啪啦地研究起组合拓扑，还弄得有模有样。
某天突然灵光一闪，他想出了一个重要的猜想，而这个猜想突然冒出了个三维反例，按照常理来讲，庞加莱应该会越加勤奋地研究这个问题，谁知道他竟然丢下这个猜想转身继续研究天体力学了。
而被丢下的庞加莱猜想在长达一个世纪里差点把后世研究它的拓扑学家搞死，直到佩雷尔曼的出现。
庞加莱提出若任意二维曲面具有与球面相等的同调群、上同调群和同伦群，那么这个曲面必然拓扑等价于球面，这就是著名的庞加莱猜想。但是当他进一步猜想这个结论对任意维空间都能成立时，出现了三维反例，而关于三维空间的证明直到2003年才被佩雷尔曼解决。
佩雷尔曼
作为一位全才，庞加莱还在物理学领域大展拳脚。
一开始，因为深入研究微分方程的需求让庞加莱注意到了三体问题，然后他发现这个三体问题还挺有趣的，就跑去参加当时举办的关于寻求n体问题的竞赛，结果他花两年写了篇论文就轻轻松松地获奖了。
幸福来得太突然很容易被戳破，当时《数学学报》的编辑在评审时发现论文中的结论是错的，于是和庞加莱书信交流了一年后，促使庞加莱得出即使其中某一天体的初始位置发生微小改变，也会是长时间演化后的结果大不相同这么一个重要结论，还顺便创造出混沌理论，至此开创了混沌学。
三体问题是天体力学中的经典问题，主要指三个质量、初始位置和初始速度都是任意的可视为质点的天体，在万有引力的作用下的位置和运动规律问题，比如太阳、地球和月亮。
现在的混沌理论已经发展成为一种质性思考与量化分析兼备的方法，一般用于探讨动态系统中（如化学反应、气象变化、股票市场等）必须用整体、连续的而非单一的数据关系才能解释和预测的行为。
然而庞加莱绝非是一个容易满足于现状的人，在接下来短短几年间他竟然奔跑在爱因斯坦的前方，抢先研究出关于相对论的理论。
庞加莱在1898年提出了光速不变性假设；1902年，阐明了相对性原理；1905年，声明物体移动不可能超过光速，简直像开了挂一样，哗啦哗啦地就成为了相对论的先驱。（棒棒的
）
当然，庞加莱的一生不只是拥有物理和数学，他还对采矿有着一辈子的爱恋。从综合工科大学毕业后他曾经跑到矿业学校学习专门的采矿知识，在研究数学的同时依旧兼顾矿业的工作，一切妥妥的。（开挂的人生无需多言）
所以说啊，智商低真的不代表什么，是牛人就能发光，任一个方面有才能分分钟能致富。
生命如此美好，依然假装充满着无限的可能性，说不定只是测试的机器刚好坏了呢。
本文由超级数学建模编辑整理
部分资料来源于网络
转载请在公众号中，回复“转载”
-----这里是数学思维的聚集地------
“超级数学建模”（微信号supermodeling），每天学一点小知识，轻松了解各种思维，做个好玩的理性派。30万数学精英都在关注！
