knn算法也称k最近邻算法
,其乃十大最有影响力的数据挖掘算法之一,该算法是一种
有监督的挖掘算法
,既可以解决离散因变量的分类问题,也可以做连续因变量的预测问题,而且该算法没有复杂的数据推导公式、更易于常人理解。接下来我们就来看看这个流行算法到底是个什么鬼?
k最近邻算法,从名称上来看还是比较容易理解的,以分类问题为例,
该算法实际上就是寻找与未知分类最近的k个已知分类训练集,然后通过投票的方式,将票数最多的那个类定性为未知分类样本
。也许你觉得这一长串话太啰嗦,还是不易理解,那我们来看一看下面这张图:
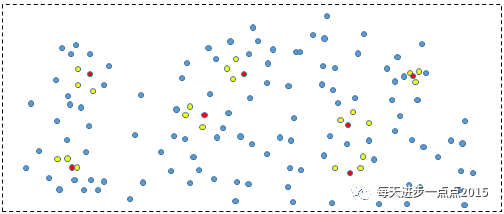
如图所示,图中
蓝色点
为已知分类的训练集,
红色点
为未知分类的测试集,如果需要得知未知分类该属于哪种类别,可以在其周围寻找最近的k个蓝色点。不妨,我们在红点周围寻找到的3个黄点即为最近的点,从而根据3个已知分类的
黄色点
来判断红点属于哪个类(投票方式)。
OK,理解了上面的过程,就是理解了knn算法的思想。既然是计算距离,那距离如何计算呢?这里可能面临着3种情况的距离计算:
1)连续变量间的距离计算?
2)离散变量间的距离计算?
3)含有缺失值的样本间距离计算?
首先我们摆出计算距离的公式,即最常用的欧式距离:
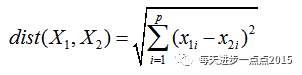
接下来我们就是利用这个公式,针对以上三种不同的情形计算观测点之间的距离。我们曾经说过,
只要跟距离相关的算法,一般都需要对原始数据进行标准化处理,目的是避免距离的值受到不同量纲的影响
。至于标准化方法,主要有两种,即Z标准化或0-1标准化处理,具体公式如下:
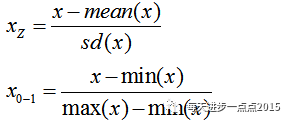
针对以上三种不同情形计算观测点之间的距离,我们利用简单的例子加以说明,目的是帮助读者有一个很好的理解。
如果手中的训练样本如下:
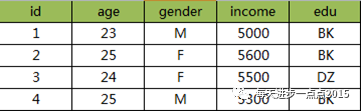
经过0-1标准化的结果为:
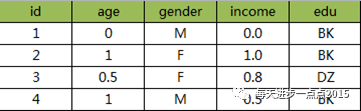
则观测1与其余观测之间的
距离可计算
为:
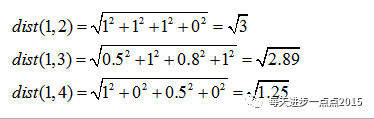
在这里给出计算方法的结论:
1)对于连续变量之间的距离
可以直接按数值差计算;
2)对于离散变量之间的距离
可以按照值是否相同计算,如果值相同则距离差值为0,否则差值为1;
3)对于离散变量(2个水平以上)
需要将其转换为哑变量,然后再
按照2)
的方法计算距离。
好了,对于第一和第二种情况的距离计算我们已轻松解决,
那如果数据中有缺失值该怎么办呢?
这里提供三种解决方案:
1)删除
缺失严重的列或删除缺失非常少的观测,然后对无缺失的情况计算距离;
2)使用替补法或多重插补法
完成缺失值的填充,然后对清洗后的数据计算距离;
3)将缺失值当作特殊值处理
,具体操作如下:
如果原始观测有缺失值,
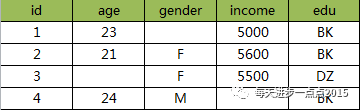
数据标准化处理的结果,
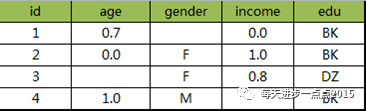
计算含缺失值的距离:
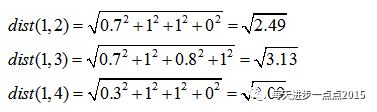
在这里给出计算方法的结论:
1)
对于离散变量
,如果两个观测存在一个或两个都是缺失,则差值为1;
2)对于连续变量
,如果两个观测都是缺失,则差值为1,如果存在一个缺失,则差值取这两个值(|1-x|和|0-x|)的最大值。
对于含缺失值的样本距离可能会稍微复杂一点,但好在三种情况的距离都可以计算。现在还存在最后一个难题,
即knn算法中的k如何确定?
到底该选择最近的几个点才合适?这个问题一旦解决,knn便可自如行走。
关于k值的确定,
一般我们会遍历k的某些值,然后从中选择误差率最低或正确率最高的k值即可
,正如下图所示:
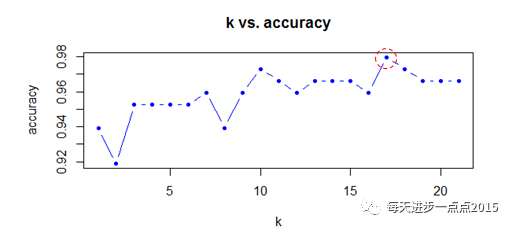
图中的红圈对应的k值即为我们所要寻找的合理值,因为在该k值下,所计算出来的模型准确率最高。
讲完了knn的思想和问题的解决方案,接下来就需要我们做一做实战的内容了,数据来源于网站http://archive.ics.uci.edu/ml/,后面也会给出数据的下载链接。在讲实战之前,需要介绍一下R落地的函数及参数含义:
knn(train,
test, cl, k = 1, l = 0, prob =
FALSE, use.all= TRUE)
train
指定训练样本集;
test
指定测试样本集;
cl
指定训练样本集中分类变量;
k
指定最邻近的k个已知分类样本点,默认为1;
l
指定待判样本点属于某类的最少已知分类样本数,默认为0;
prob
设为TRUE时,可以得到待判样本点属于某类的概率,默认为FALSE;
use.all
控制节点的处理办法,即如果有多个第K近的点与待判样本点的距离相等,默认情况下将这些点都纳入判别样本点,当该参数设为FALSE时,则随机挑选一个样本点作为第K近的判别点。
实战:乳腺癌诊断
#数据读取
cancer
sep = ',')
#给原始数据编辑变量名

#数据探索
dim(cancer)
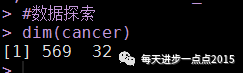
该数据集含有569个样本和32个变量。
str(cancer)
summary(cancer)
从运行结果看(这里没有将结果贴出了,需要读者自己运行试试),数据集中不含有缺失值,除Diagnosis变量外,其余变量均为数值型变量,ID变量为编号,没有任何意义,故在建模过程中将删除该变量。发现各个变量间存在明显的量纲大小,需要进一步对原始数据进行标注化。
#构建标准化函数
standard
(x-mean(x))/sd(x)
}
#将该函数应用到数据框cancer中的每一列(除Diagnosis变量)
cancer_standard
summary(cancer_standard)
#将数据框cancer中的Diagnosis变量合并到cancer_standard中
cancer_standard
names(cancer_standard)[1]
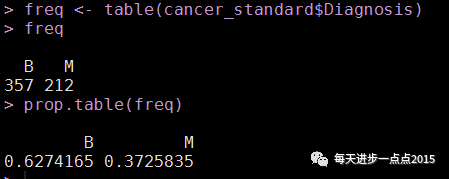
Diagnosis变量为因子变量,表示诊断结果,M表示恶性,B表示良性。我们初步查看一下这两个水平的统计结果。
freq cancer_standard$
Diagnosis)
prop.table(
freq
)
#构建训练集、测试集和验证集
set.seed(1)
index
train
test
训练集和测试集已经抽样完毕,接下来我们需要查看训练集和测试集中因变量的比重是否与总体吻合,从而看抽样是否具有代表性
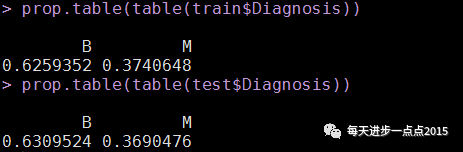
抽出来的效果还不错,训练集和测试集的因变量比例与总体因变量比例大体相当。
#构建模型,以循环的方式选择knn算法中的k值
library(class)
res = NULL
for (i in 1:round(sqrt(nrow(train)))){
model
Freq
accu
res
}
plot(1:round(sqrt(nrow(train))),res,type = 'b', pch = 20, col= 'blue',
main = 'k vs. accuracy',
xlab = 'k', ylab = 'accuracy')
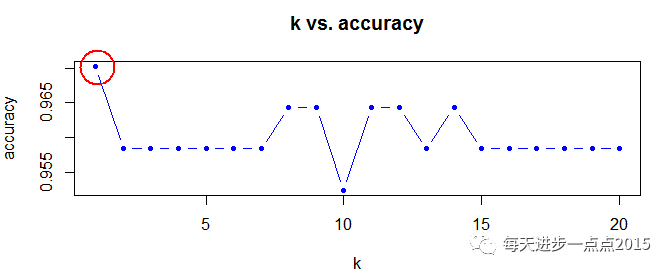
我的天呐,当k等于1时,模型的准确达到了最高,那么我们就不妨使用k=1,作为knn算法的参数。















