有部分数列的通项公式根据脚标为奇数、偶数而有所不同,称为数列的奇偶项问题.
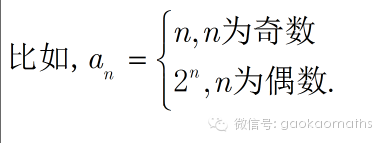
解题过程中,通常要采用奇偶分析法,即对脚标的奇偶分类讨论.
实栗分析:隔项等差数列
看2014年全国高考卷的一道数列题.

分析:题中给出的是通项与前n项和的关系.童鞋们对这种题型训练的较多,基本的办法就是利用二者的关系,把前n项和消去,得到相邻两项或相邻多项的关系.

从(1)问的结论中,我们能判断数列为等差吗?
显然不能,因为等差数列要求后项减去前项是同一个常数,而上式中两项的脚标相差2.
当然,我们可以这样来看:
第一项,第三项,第五项,...,即奇数项可看作等差数列;第二项,第四项,第六项,...即偶数项可看作等差数列
.
但是,我们不能认为整个数列为等差数列
.
特值法:研究隔项等差数列成为完整等差数列的条件
第(2)为探索题.对于探索题的解法,通常我们先假设存在,用特殊项,比如利用前3项成等差,求出参数的值(这个过程利用的是条件的必要性);然后再验证该参数的值的确使得该数列为等差数列(这个过程是证明条件的充分性).
这种先用特殊法求值,再一般验证的办法,有利于减少探索时间,这在高考时间紧迫的情况下尤其显得重要
.

当然,解到这一步不算完,入=4是必要条件,我们还要验证这个条件是充分的——即说明当
入=4时,该数列的确是完整的等差数列.
如何验证呢?
证明数列为等差的途径有以下几个.

其中,1是定义法,4是中项法,
2和3是定义法的拓展和延伸,2称为通项判断法,3称为前n项和判断法.
2和3分别试图从通项和前n项和的形式上描述等差数列,当然方法2和3本质上依然是定义法.
结合第(1)问提供的结论,我们采用通项判断法.为此需要研究数列的通项公式,为此需要采用奇偶分析法.

同样的方法研究偶数项的通项公式.

我们看到,不管n为奇数还是偶数,通项公式的形式是相同的.

在采用奇偶分析法研究数列的通项时,我们采用了
累加法
.这个方法简单易用,属于“无脑解法”,不容易犯错.
当然,因为奇数项成等差,偶数项也成等差,你也可以利用等差数列的通项公式直接写出奇数项和偶数项的通项公式,前提是
项数不要搞错.
推广:隔项等差数列成为完整等差数列的一般条件
下面,思考一个一般化的问题.

请思考2分钟,再往下看.





