
撰文 | ben助教
编辑 | Francesca jin
专栏 | 九章算法
对n个数的序列,a1,a2,……,an,判断是否存在i
样例1
输入: [1,2,3,4]
输出: False
样例2
输入: [3,1,4,2]
输出: True
说明: [1,4,2]是一个132模式
样例3
输入: [-1,3,2,0]
输出: True
说明: [-1,3,2],[-1,3,0],[-1,2,0]均为132模式
枚举i
a. 令min(j)为a(1),a(2),……,a(j)中的最小值,那么如果[a(i),a(j),a(k)]为一个132模式,则[min(j-1),a(j),a(k)]也必为132模式,反之,如果[min(j-1),a(j),a(k)]不是132模式,那么对于任意i
b. min(j)可以用O(n)的时间递推出来,再枚举j,k,判断是否有min(j-1)
a.与方法2相似,我们也可以省去对k的枚举。令max(j)为a(j+1),a(j+2),……,a(n)中小于a(j)的最大值,那么a(k)即可用max(j)代替。与方法2中不同的是,此处要求的不是a(j)以后的数中的最大值,而是要小于a(j)的最大值,这个问题当然可以用线段树或者平衡树来处理,但过于复杂,其实用栈就可以处理这个问题。
b. 我们从后往前枚举j,如果栈顶元素小于a(j),则将栈顶元素出栈,直到栈为空或栈顶元素不小于a(j),再将a(j)压入栈。这样就保证了,栈中元素由栈顶到栈底是非降序的,那么在a(j)入栈前最后一个出栈的就是栈中小于a(j)的最大值。
c. 有一个小问题是,实际的max(j)可能在枚举到j之前就已经出栈了,而导致实际得到的值并非是a(j)以后小于a(j)的最大值,而只是枚举到j时的栈中小于a(j)的最大值,但这对于原问题的求解来说没有影响,故仍把该值记为max(j),有兴趣的读者可以自己分析一下。
d. 得到max(j)后,判断是否有min(j-1)
Follow up:如何快速统计序列中132模式的组数?
这里提供一个思路:从后往前枚举i,同时维护一组键值对{a(k),ans(k)},ans(k)表示满足ia(k)的组数,故a(i)对答案的贡献为所有大于a(i)的a(k)对应的ans(k)之和;加入a(i)后,则将对所有小于a(i)的a(k)对应的ans(k)增加1,同时增加一组键值对{a(i),0}。
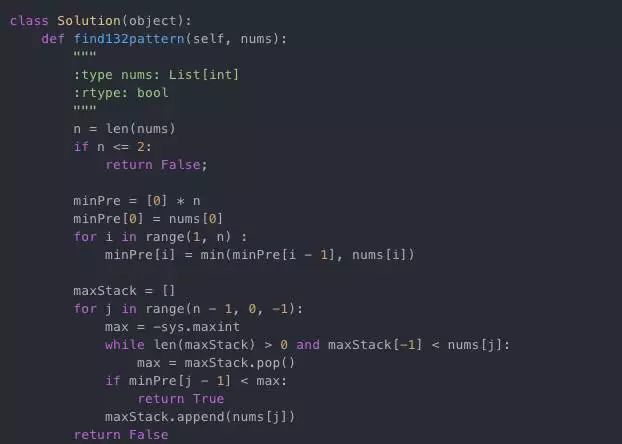
这个问题主要考察对问题的分析预处理的能力,三种不同时间复杂度的算法可以把面试者分成三类,是一道适合面试的好题。给出第二种算法可以hire,给出第三种可以strong hire。
http://www.lintcode.com/zh-cn/problem/implement-stack/
http://www.jiuzhang.com/solution/132-patterns/
回复“简历”,查看简历撰写指南,获取“简历模板”
回复“冷冻期”,查看北美各大IT企业冷冻期信息和注意事项
回复“Career”, 查看Caireer Fair 攻略 check list
回复“薪资”,查看北美各大IT企业New Grades Engineer 薪资水平;
回复“项目”,查看7-14天可以搞定的小项目推荐
回复“评分”,查看系统设计评分指南
回复“behavior”,查看behavior interview指南
回复“晋升”,查看Engineer晋升机制
算法强化班 | 面向Facebook/Google等求职者
各类IT企业的面试算法难度及风格
如何解决中等难度以上的算法题
如何解决follow up问题
正在报名中!
报名登陆官网 www.jiuzhang.com
或点击文末“阅读原文”

















