邢不行是经管之家「量化投资」版块的版主,毕业于香港科技大学,热门教程《量化小讲堂》的作者。
上周邢老师分享了十分接地气的量化炒股方法:一个10年翻400倍的投资策略 |python量化系列
这次邢老师给大家分享一个获得过诺贝尔奖的高大上炒股方式。
假设你有一笔钱准备投资股票,你从A股三千多只股票中挑选了50只,准备作为一个投资组合购买。
那么在这50只股票之间应该如何分配仓位呢?是将资金均分成50份然后每个股票各买20万,还是有的股票多买点有的股票少配点呢?
如何在这些股票之间分配仓位,这个问题就是马克维茨(Harry Markowitz)在1952年用数学解决的问题。他也因此而拿到了诺贝尔经济学奖。

马克维茨
马克维茨提出的解决方案被后世称为资产组合理论,开创了近代金融学。 本文尝试:
理论:从三个股票说起
假设有3只股票A、B、C。其中股票A,在一年后有一半概率上涨20%,一半的概率上涨10%,那么它的期望收益是15%(20% * 0.5 + 10% * 0.5 = 15%)。
股票B、股票C的涨跌概率以及期望收益,如下图所示:
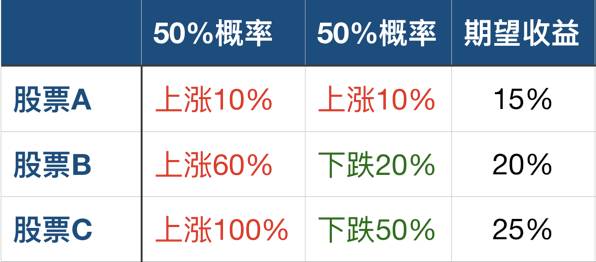
若在这3个股票中选择1个股票买入,你会选择哪个呢?
选择股票A的人偏保守,虽然赚的少一点,但毕竟风险低,任何情况下都是稳赚。
选择股票B,差的情况只亏20%,好得情况却可赚60%,相当不错的选择。
选择股票C就是富贵险中求,虽然风险高,可能亏去一半,但是翻倍的诱惑也是巨大的。
汝之蜜糖彼之砒霜,其实选择哪个股票都是正常的。
理论:收益和风险
在这3个股票中进行选择,其实我们是在权衡收益和风险。我们希望收益越高越好,风险越低越好。
然而金融领域自打有宇宙以来的第一定律就是高收益和低风险不可兼得。收益高,往往风险也高,风险低往往收益也就低了。
所以我们只能根据自己的偏好在收益和风险之间进行权衡,做出最优选择。要进行权衡,必然要先将收益和风险进行量化。
前文中我们用期望收益来量化收益,那用什么方式来量化风险呢?
用方差!
对,就是初中学习过的方差。方差用来描述一组数据的离散程度,而收益的离散程度就是风险。
比如对于股票A,它的方差就是[(0.2 - 0.15)^2 + (0.1 - 0.15)^2] / 2 = 0.0025。同理,股票B和股票C的方差是0.16和0.5625。股票的风险越大,它的方差也就越大,反之,方差大说明这个股票的风险也大。
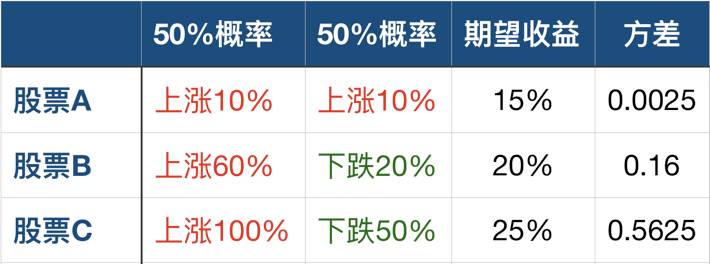
理论:将股票进行组合?
知道如何量化收益和方差后,我们回到A、B、C三个股票上来。如果做一个投票,可能很多人会选择方案B,赚得多赔的少。
但是B真的是最好的选择吗?其实还有更好的选择,比如:将所有钱中的一半买股票A,另一半买C,形成一个组合。
这个组合一年后的收益情况如下图:
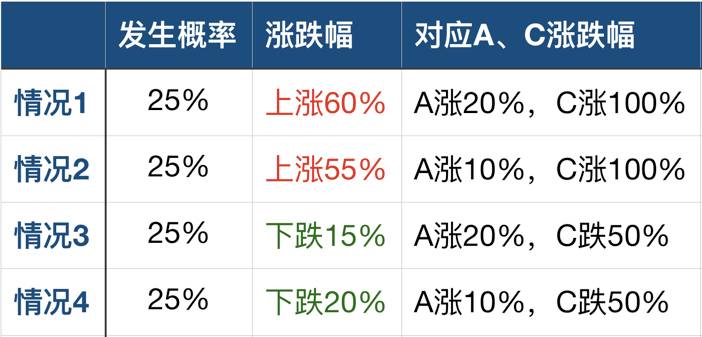
该组合的期望收益是20%,跟B一样。但是组合的方差约为0.14,比B的0.16要小。
也就是说我们通过构建一个组合,得到了一个和B收益一样,但是风险比B小的投资。
那么很显然,相比于这个组合,只买B就是一个愚蠢的选择。
这就是投资组合的威力。
这时候聪明的你一定会问:刚刚平分仓位于A、C构建组合,那么是否存在另外的分配方式,使得该组合在20%的期望收益下,风险(方差)可以更小呢?
或者说我能接受方差为0.1的风险,怎么在3只股票里面分配仓位,可以保证期望收益最大呢?
感兴趣的话可以动笔算算,真的很有意思。
理论:我也能拿诺奖?
其实以上这些问题就是马克维茨当年想要解决的问题。
如何在一堆股票当中通过分配仓位,来使整个组合的期望收益尽可能的高,风险(方差)尽可能的低。或者说,在一定的期望收益下,风险尽可能的低;在一定的风险下,期望收益尽可能的高。
这时候有的朋友可能会说,这看上去也没什么难度嘛,就算是离诺奖无穷远的我,多花点时间也能算来。
是的,以上的计算确实并不复杂。那是因为我们在计算当中想当然的多增加了一个条件——
我们假设这些股票之间的收益是相互独立的,也就是股票和股票之间的收益不会相互影响。
然而现实中所有股票之间都是相关的啊!
有过投资经验的人都知道,工商银行股票上涨的时候,农业银行大概率也会上涨吧?因为互为竞争关系,京东股票上涨,阿里的股票倾向于下跌吧?这些都说明股票之间存在相关性。
所以上面A、B、C三只股票的问题,可能会变成股票A上涨的时候,股票B也有80%的概率上涨;股票A上涨的时候,股票C却有60%的概率下跌。这个时候想要算出最优仓位比例,就比较麻烦了吧?
而人家马克维茨牛就牛在,即使考虑了股票之间的相关性,他也找到了计算的方法。
马克维茨使用相关系数来衡量股票之间的相关性,再结合之前的期望收益、方差,仅仅知道这些,就可以计算出最优的仓位比例,来保证我们的投资组合获得尽可能高的收益以及相应尽可能低的风险。
具体怎么计算这里就不细说了,归根到底是一个标准凸二次规划问题。
接下来我们就用历史数据和python,来验证下拿了诺贝尔奖的理论,在实际投资中是否有用。
实战:全球投资
马克维茨的理论在实际投资当中最经典的应用就是资产的全球化配置。
假设我们有一笔资产想要在全球众多投资品种之间进行投资,例如股票、债券、大宗商品等。目标是希望在保值的前提下,获取比简单理财产品高的收益。
那此时就可以使用马克维茨的理论来进行仓位分配了。为了方便起见,我们选取股票、债券、大宗商品这三类资产,并用其对应的指数作为代表,来进行实验。
即假设我们是要投资这些指数,并在这些指数之间分配仓位。具体的资产以及对应指数见下图:
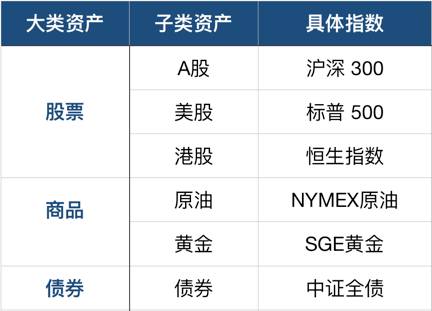
实战:具体策略
用马克维茨的模型,最大的难点就是要确定模型的输入参数。必须知道这些资产未来的期望收益、方差及相关系数才能计算最终的仓位,可是未来发生的事情,我们现在怎么可能知道呢?
实战中一般的做法就是拿过去一段时间的数据来估计这些参数。落实到具体的策略,我们采用如下方法。
在每月的最后一个交易日,根据过去12个月的历史数据计算出每个指数的收益、方差、相关系数。将这些数据作为参数,套入模型中,计算出每个指数的仓位。
按计算出来的仓位买入这些指数并持有整个下个月。在下月末再按照该方法进行调整,如此往复。
其中在计算最优仓位的时候,我们对原始模型进行了微调。优化目标是在组合每月最大跌幅不超过2%(95%置信区间)的条件下,最大化组合的预期收益。
实战:结果
若从2014年开始,我们按照上述的策略进行投资,可以得到如下的结果。
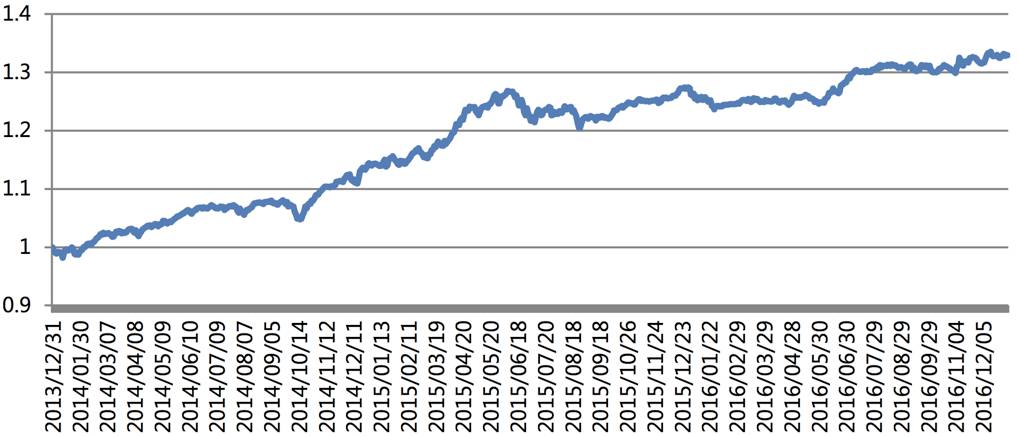
资金曲线
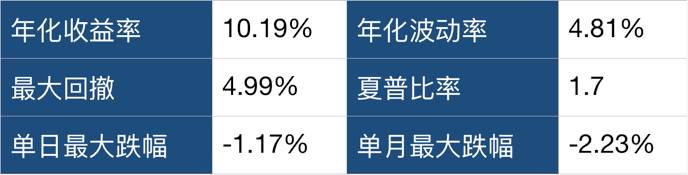
策略评价指标
由图中可以看到,假设我们初始持有1元钱,到2016年末,它会变成1.34元。累计增长了34%,年化收益10.19%,远高于一般的理财收益。
更加关键的是,整个策略的资金曲线非常的平稳,说明策略的风险很低。其中单月最大的跌幅是2.23%,几乎可以忽略不计。
较高的收益,较低的风险,这确实是一个相当好的投资策略。
如果需要数据、代码以及马克维茨论文原文,可根据文末提示加邢老师微信询问。
邢老师的python量化入门课程
邢老师经过多轮直播,精心打磨的《python量化投资入门》视频课程,也在最近上线了!
主讲老师邢不行,全额奖学金毕业于香港科技大学,经管之家(原人大经济论坛)「量化投资」版块的版主,拥有多年量化投资实战经验。
课程大纲、更多介绍,请长按下图识别二维码查看:
















