1.朴素贝叶斯算法核心思想

贝叶斯分类是一类分类算法的总称 ，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而 朴素贝叶斯（Naive Bayes）分类是贝叶斯分类中最简单，也是常见的一种分类方法 。

朴素贝叶斯算法的核心思想是通过考虑特征概率来预测分类，即对于给出的待分类样本，求解在此样本出现的条件下各个类别出现的概率，哪个最大，就认为此待分类样本属于哪个类别。

举个例子：眼前有100个西瓜，好瓜和坏瓜个数差不多，现在要用这些西瓜来训练一个『坏瓜识别器』，我们要怎么办呢？

一般挑西瓜时通常要『敲一敲』，听听声音，是清脆声、浊响声、还是沉闷声。所以，我们先简单点考虑这个问题，只用敲击的声音来辨别西瓜的好坏。根据经验，敲击声『清脆』说明西瓜还不够熟，敲击声『沉闷』说明西瓜成熟度好，更甜更好吃。

所以，坏西瓜的敲击声是『清脆』的概率更大，好西瓜的敲击声是『沉闷』的概率更大。当然这并不绝对——我们千挑万选地『沉闷』瓜也可能并没熟，这就是噪声了。当然，在实际生活中，除了敲击声，我们还有其他可能特征来帮助判断，例如色泽、跟蒂、品类等。

朴素贝叶斯把类似『敲击声』这样的特征概率化，构成一个『西瓜的品质向量』以及对应的『好瓜/坏瓜标签』，训练出一个标准的『基于统计概率的好坏瓜模型』，这些模型都是各个特征概率构成的。

这样，在面对未知品质的西瓜时，我们迅速获取了特征，分别输入『好瓜模型』和『坏瓜模型』，得到两个概率值。如果『坏瓜模型』输出的概率值大一些，那这个瓜很有可能就是个坏瓜。

2.贝叶斯公式与条件独立假设

贝叶斯定理中很重要的概念是 先验概率 、 后验概率 和 条件概率 。（关于这部分依赖的数学知识，大家可以查看ShowMeAI的文章 图解AI数学基础 | 概率与统计，也可以下载我们的速查手册 AI知识技能速查 | 数学基础-概率统计知识）(链接见文末)。

1）先验概率与后验概率

先验概率 ： 事件发生前的预判概率 。可以是基于历史数据的统计，可以由背景常识得出，也可以是人的主观观点给出。一般都是单独事件概率。

举个例子：如果我们对西瓜的色泽、根蒂和纹理等特征一无所知，按照常理来说，西瓜是好瓜的概率是60%。那么这个概率P（好瓜）就被称为先验概率。

后验概率 ： 事件发生后求的反向条件概率 。或者说，基于先验概率求得的反向条件概率。概率形式与条件概率相同。

举个例子：假如我们了解到判断西瓜是否好瓜的一个指标是纹理。一般来说，纹理清晰的西瓜是好瓜的概率大一些，大概是75%。如果把纹理清晰当作一种结果，然后去推测好瓜的概率，那么这个概率P（好瓜|纹理清晰）就被称为后验概率。

条件概率 ：一个事件发生后另一个事件发生的概率。一般的形式为 表示 发生的条件下 发生的概率。

2）贝叶斯公式

简单来说，贝叶斯定理（Bayes Theorem，也称贝叶斯公式）是基于假设的先验概率、给定假设下观察到不同数据的概率，提供了一种计算后验概率的方法。在人工智能领域，有一些概率型模型会依托于贝叶斯定理，比如我们今天的主角『朴素贝叶斯模型』。

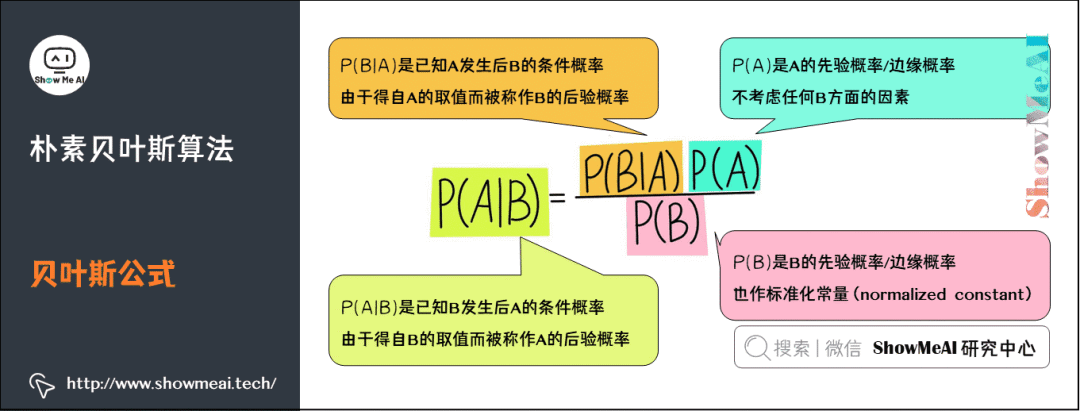
是先验概率，一般都是人主观给出的。贝叶斯中的先验概率一般特指它。

是先验概率，在贝叶斯的很多应用中不重要（因为只要最大后验不求绝对值），需要时往往用全概率公式计算得到。

是条件概率，又叫似然概率，一般是通过历史数据统计得到。

是后验概率，一般是我们求解的目标。

3）条件独立假设与朴素贝叶斯

基于贝叶斯定理的贝叶斯模型是一类简单常用的分类算法。在『假设待分类项的各个属性相互独立』的情况下，构造出来的分类算法就称为朴素的，即朴素贝叶斯算法。

所谓『朴素』，是假定所有输入事件之间是相互独立 。进行这个假设是因为独立事件间的概率计算更简单。

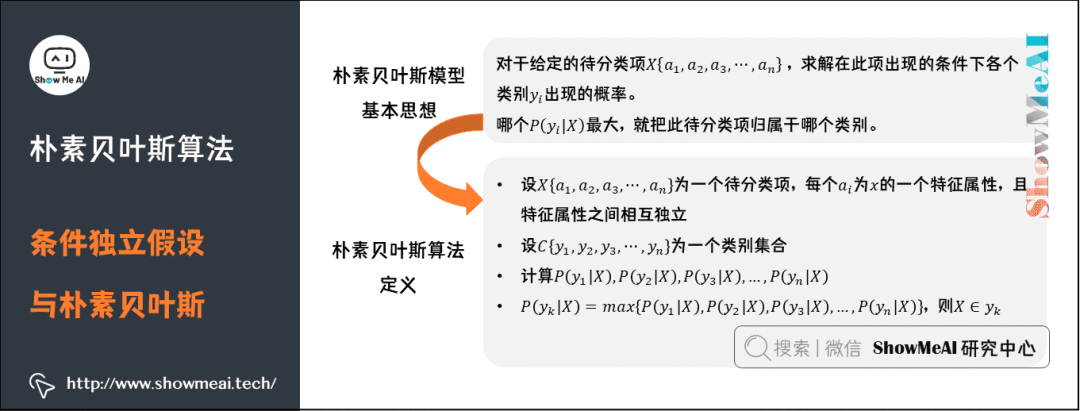
朴素贝叶斯模型的基本思想是：对于给定的待分类项 ，求解在此项出现的条件下各个类别 出现的概率，哪个 最大，就把此待分类项归属于哪个类别。

朴素贝叶斯算法的定义为：设 为一个待分类项，每个 为x的一个特征属性，且特征属性之间相互独立。设 为一个类别集合，计算 。

则

要求出第四项中的后验概率 ，就需要分别求出在第三项中的各个条件概率，其步骤是：

在朴素贝叶斯算法中，待分类项的每个特征属性都是条件独立的，由贝叶斯公式

因为分母相当于在数据库中 存在的概率，所以对于任何一个待分类项来说 都是常数固定的。再求后验概率 的时候只用考虑分子即可。

因为各特征值是独立的所以有：

可以推出：

对于 是指在训练样本中