漫谈真空中光速的精密测量

在光的传播速度是否有限的问题上，物理学界曾经有过争执，德国天文学家开普勒和法国数学家笛卡尔都认为光的传播不需要时间，是在瞬时进行的。但意大利的物理与天文学家伽利略却认为光速虽然传播得很快，但却是有限，并可以测定的。这三位伟大的科学家(图1)的争论，伽利略准备用实验来给以回答。

图1 (a)开普勒(1571—1630)；(b)笛卡尔(1596—1650)；(c)伽利略(1564—1642)

1.1 伽利略的测量试验

1607 年，36 岁的伽利略进行了世界上第一个测量光速的实验。为了使光能飞行较远的距离，他将测量的地点设在郊外的山上。伽利略的方法是，让两个人分别站在相距1 英里(约1.6 km)的两座山上，每个人拿一个灯，第一个人先举起灯，当第二个人看到第一个人的灯时立即举起自己的灯，从第一个人举起灯到他看到第二个人的灯的时间间隔就是光传播两英里的时间。但由于光速传播的速度实在是太快了，这种方法根本行不通。但伽利略的实验揭开了人类历史上对光速进行研究的序幕。

1.2 罗麦的木星卫星食推算

1676 年，丹麦天文学家罗麦第一次提出了有效的光速测量方法。他在观测木星的卫星的隐食周期时发现：在一年的不同时期，它们的周期有所不同；在地球处于太阳和木星之间时的周期与太阳处于地球和木星之间时的周期相差十四、五天。他认为这种现象是由于光具有速度造成的，而且他还推断出光跨越地球轨道所需要的时间是22 分钟。1676 年9 月，罗麦预言预计11 月9 日上午5 点25 分45 秒发生的木卫食将推迟10 分钟，其测量示意图见图2。巴黎天文台的科学家们怀着将信将疑的态度，观测并最终证实了罗麦的预言。

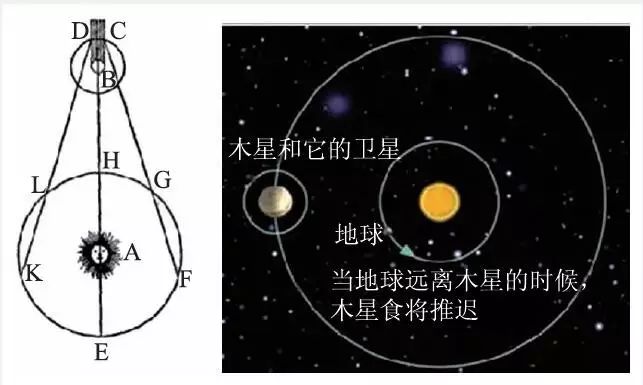
图2 罗麦用木星的卫星食测量光速示意图(左图中A为太阳，H为地球，B为木星，C和D为木星的卫星)

罗麦的理论没有马上被法国科学院接受，但得到了著名科学家惠更斯的赞同。惠更斯根据他提出的数据和地球的半径第一次计算出了光的传播速度：214000 km/s。虽然这个数值与目前测得的最精确的数据相差甚远，但它启发了惠更斯对波动说的研究；更重要的是这个结果的错误不在于方法的错误，只是源于罗麦对光跨越地球的时间的错误推测，现代用罗麦的方法经过各种校正后得出的结果是298000 km/s，很接近于现代实验室所测定的精确数值。

1.3 布莱德雷的恒星的“光行差”计算

1725 年，英国天文学家布拉德雷发现了恒星的“光行差”现象，以意外的方式证实了罗麦的理论。刚开始时，他无法解释这一现象，直到1728 年，他在坐船时受到风向与船航向的相对关系的启发，认识到光的传播速度与地球公转速度共同引起了“光行差”的现象。他用地球公转的速度与光速的比例估算出了太阳光到达地球需要8 分13 秒。这个数值较罗麦法测定的要精确一些。布莱德雷测定值证明了罗麦有关光速有限性的说法。布莱德雷发现的恒星的“光行差”现象如图3所示。

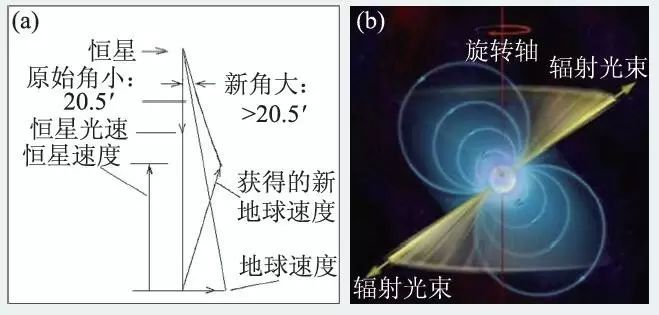
图3 布莱德雷发现的恒星“光行差”现象示意图(a)考虑到太阳速度进入视野略图；(b)恒星速度与地球速度略图

光速的测定，成了17 世纪以来所展开的关于光的本性的争论的重要依据。但是，由于受当时实验环境的局限，科学家们只能以天文学方法测定光在真空中的传播速度，还不能解决光受传播介质影响的问题，所以关于这一问题的争论始终悬而未决。

18 世纪，科学界是沉闷的，光学的发展几乎处于停滞的状态。继布莱德雷之后，经过一个多世纪的酝酿，到了19 世纪中期，才出现了新的科学家和新的方法来测量光速。

1.4 斐索的旋转齿轮法

1849 年9 月，法国实验物理学家斐索第一次在地面上设计实验装置，用旋转齿轮法来测定光速(图4)。他的方法原理与伽利略的相类似。

图4 斐索用旋转齿轮法测定光速示意图

在图4 中，光自垂直于图面的狭缝状光源s 出发，经过透镜L和有半镀银面的平板M₁，而会聚于F 点。在F 点所在的平面内，有一个旋转速度可变的齿轮W，它的齿隙不遮光，而它的齿却能遮住所有会聚于F 点的光。通过齿隙的光，经过透镜L₁后成为平行光，透镜L₂将此平行光会聚在它自己焦点上的凹面反射镜M₂的表面上。光至反射镜M₂后被反射沿原路回来。如果在光由F点到M₂的一个往返的时间间隔Δt 内，齿轮所旋转的角度正好使齿隙被齿所代替，则由M₂反射回的光受阻，在透镜L₃后的E处看不见光；反之，如果齿隙被另一齿隙所代替，则在E处能看见由M₂反射回来的光。这样，当齿轮转速由零而逐渐加快时，在E 处将看到闪光。当齿轮旋转而到达第一次看不见光的位置时，必定是图4 中的齿隙1 为齿a 所代替。设齿轮此时的转速为每秒v 圈，齿数为n，则a转到1所需的时间间隔为

Δt = 1/2nv.   (1)

另一方面，在此时间内，光由F 到M₂(路程为L)，又由M₂返回到F，一共走了路程2L，即

Δt = 2L/c，   (2)

比较以上两式，则有

c=4nLv .      (3)

斐索用齿数为720 的齿轮，取2L 等于1.7266×10⁵ m，发现第一次看不见光时齿轮的旋转速度为每秒12.6 圈，测得光速为3.15×10⁸ m/s。这个实验中主要的误差是很难精确地确定看不见光的条件，因为齿有一定的宽度，当F 不正好在齿的中央时，光也能被遮住。斐索之后，还有纽考姆(Newcomb)，福布斯(Forbes)，以及珀罗汀(Perotin)等人先后改进了这个实验，所得结果均在2.99×l0⁸—3.01×10⁸ m/s的范围内。

1.5 傅科的旋转镜法

1850 年，法国实验物理学家傅科改进了斐索的方法，他只用一个透镜、一个旋转的平面镜和一个凹面镜。平行光通过旋转的平面镜汇聚到凹面镜的圆心上，同样用平面镜的转速可以求出时间。傅科用这种方法测出的光速是298 000 km/s。此外，傅科还测出了光在水中的传播速度，通过与光在空气中传播速度的比较，他测出了光由空气射入水中的折射率。

旋转镜法的主要特点是能对信号的传播时间作精确测量，1851 年傅科成功地运用此法测定了光速。旋转镜法的原理早在1834 年至1838 年就已由惠根斯和阿拉果提出过，它主要用一个高速均匀转动的镜面来代替齿轮装置。由于光源较强，而且聚焦得较好。因此能极其精密地测量很短的时间间隔。实验装置如图5所示。

图5 傅科的旋转镜法实验装置(图中D为旋转镜与固定镜之间的距离，θ为光的入射线与旋转镜之间的夹角)

19 世纪末，旋转镜法获得的光速结果有：1879 年和1883 年迈克尔孙的测量值分别为c=299910±75 km/s 和c=299853±90 km/s；1883 年纽考姆的测量为c=299860±45 km/s。

1.6 迈克尔逊的旋转棱镜法

美国的迈克尔逊把齿轮法和旋转镜法结合起来，创造了旋转棱镜法装置。齿轮法之所以不够准确，不仅是由于当齿的中央将光遮断时变暗，而且当齿的边缘遮断光时也变暗。因此不能精确地测定像消失的时刻。旋转镜法也不够精确，因为在该法中像的位移Δs 太小，只有0.7 mm，不易测准。迈克尔逊的旋转镜法克服了这些缺点。他用一个正八面钢质棱镜代替了旋转镜法中的旋转平面镜，从而使光路大大增长，并利用精确测定的棱镜的转动速度代替齿轮法中的齿轮转速，测出了光走完整个路程所需的时间，从而减少了测量误差。

迈克尔逊利用多面反射镜代替傅科法中的单个反射镜M₁，在1926 年做出图6 所示的实验装置。光从狭缝状光源S 发出，在一旋转的八面棱镜的一面上发生反射，再经两个固定的平面镜M₂和M₃ 反射到大凹面镜M₄(焦距约18 m，孔径约60 cm)。M₄把光变成平行光送至与M₄相距约35 km的M₅上，M₅与M₄相似。M₅把光会聚于一小平面镜M₆，再从这里经过M₅，M₄，M_3′ (在M3 的下方)，M_2′和棱镜的面，而到达观察者的眼睛E处。

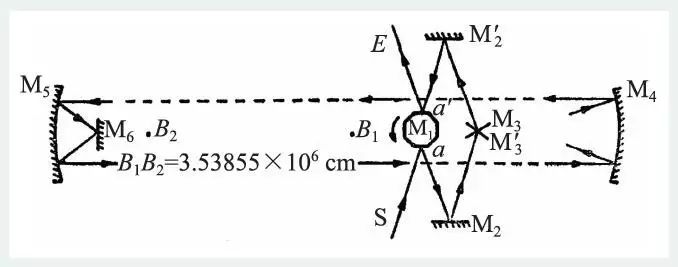
图6 迈克尔逊的旋转棱镜法测光速示意图(B₁和B₂之间的距离为3.53855×10⁶cm)

从1879 年至1926 年，迈克尔逊曾前后从事光速的测量工作近五十年，在这方面付出了极大的劳动。1926年他的光速测定值为

c=299796 km/s .

这是当时最精确的测定值，很快成为当时光速的公认值。

光速测定的天文学方法和大地测量方法，都是采用测定光信号的传播距离和传播时间来确定光速的。这就要求要尽可能地增加光程，改进时间测量的准确性。这在实验室里一般是受时空限制的，而只能在大地野外进行，迈克尔逊当时是在相距35373.21 m的两个山峰上完成光速测定的。

1.7 理论和实验推测光速的数值

20 世纪初，在诸多科学家争相测量光速之时，有两位科学家从理论上推算了光速的数值。1906 年，罗萨(E.B.Rosa)和窦赛(N.E.Dorsey)发表了一个准确的光速值：299784±15 km/s。他们通过测量两类电单位之比，即绝对静电单位(esu)中的电荷与绝对电磁单位(emu)的同一电荷之比获得的。美国国家标准局非常仔细地进行了这项实验。1941年，伯奇(R.T.Birge)评论此实验为“整个科学史上精密研究中完成的最美的实验之一”。值得关注的是，二人的光速值处于当时光速测量值的中间， 与当时老值(299774 km/s) 和新值(299793 km/s)均仅相差9 km/s。

1.8 克尔盒法

1924 年，卡罗卢斯(Karolus)和米特尔施泰特(Mittelstaedt) 提出利用克尔盒法来测定光速。1934 年，谷瑞·德布雷(Cheury de Brayza)发表了有关光速的文章，其中列出了他们几年间光速的测量结果：1924 年的结果为299802(30) km/s；1926 年的结果为299796(4) km/s；1928 年他们发表的结果，在测量中使用了克尔盒法，但最终施加交变电压来代替齿轮，用以周期性地隔断光束，由此得到的光速值是755 次测量结果的平均值，为299778(20) km/s；1933 年的结果为299774(2) km/s。

1937 年，安德森在发现正电子获1936 年诺贝尔物理学奖后，也用克尔盒法测量光速，他与另一位科学家胡特尔(Huttel)的测量结果和不确定度不谋而合，均为299771(15) km/s。但在1941年，安德森的测量结果为299776(9) km/s，不确定度从5×10^-3降低到1.4×10^-5。

1951 年，瑞典的贝奇斯传德(E.Bergstrand)用克尔盒法测出的光速是299793.1(0.32) km/s，1953 年，麦肯济(Mackenzie)用此法测出的光速是299792.4(0.5) km/s，二者的不确定度分别为0.32×10^-5和0.5×10^-5。

2.1 微波谐振腔法

光波是电磁波谱中的一小部分，当代人们对电磁波谱中的每一种电磁波都进行了精密的测量。当它的频率为某一值时发生共振。1950 年，埃森(Essen)提出用空腔共振法来测量光速。这种方法的原理是，微波通过空腔时，根据空腔的长度可以求出谐振腔的波长，再把谐振腔的波长换算成光在真空中的波长，由波长和频率的乘积可计算出真空中光速。在他的实验中，将微波输入到圆柱形的谐振腔中，当微波波长和谐振腔的几何尺寸匹配时，谐振腔的圆周长πD(D为谐振腔直径)和波长λ之间有如下的关系：πD=2.404825 λ，因此可以通过谐振腔直径的测定来确定波长，而直径D 则用干涉法测量；频率用逐级差频法测定。测量精度达10^-7。在埃森的实验中，所用微波的波长为10 cm，所得光速的结果为299792.5±1 km/s 。

2.2 微波干涉仪法

当代计算出的最精确的光速都是通过波长和频率求得的。1952 年至1954 年，英国国家物理研究所(NPL)的弗洛姆(Froome)用微波干涉仪测定了真空中光速值；1958 年，在改进后用频率约为72 GHz(波长4 mm)的微波干涉仪得出真空中光速的精确值为299792.50 ± 0.10 km/s(0.33 ppm) 。1967 年，原苏联的西姆金(Simkin)等人用频率约为36 GHz(波长8 mm)的微波干涉仪完成了类似的测定，得到真空中光速的精确值为299792.56±0.11 km/s(0.37 ppm)。

2.3 光电测距仪法

用光在被测基线(约10 km)内的飞行时间测定，这是当初伽利略试验的发展。1949 年至1957年，瑞典的贝奇斯传德采用了光电测距仪的方法，他用经过调制的克尔盒作为光源，用同一振荡器调制的光电倍增管作为检测器，其测定结果与1965 年寇利巴叶(Kolibayev)和1967 年格汝斯(Grosse)的测定结果分别为299793.1(0.32) km/s；299792.6(0.25) km/s和299792.6(0.05) km/s。

2.4 其他方法

20 世纪50-60 年代，光速测量的结果此起彼伏，先后出现红外旋转光谱法、固有长度谐振腔法、可变长度谐振腔法、基线雷达测量法等，如1949 年和1951 年Aslacson 用基线雷达测量法的测定结果分别为299792.4(3.6) km/s和299794.2(2.8) km/s 。

2.5 光速测量历史上的重大突破

1973 年，美国NBS 的埃文森(K.M.Evenson)等人率先发表了88 THz甲烷谱线的频率测量结果。他们完成了第一个从微波频率延伸到甲烷谱线的光频标准测量链，图7 列出了测量方框图。图中右上方所示的是3 台饱和吸收稳定的激光器，中间的HCN激光器和H₂O激光器是过渡激光器，左上方3 台激光器是偏频锁定激光器，它们的频率与稳定激光器的频率的固定频差为几兆赫量级，但不存在频率调制。

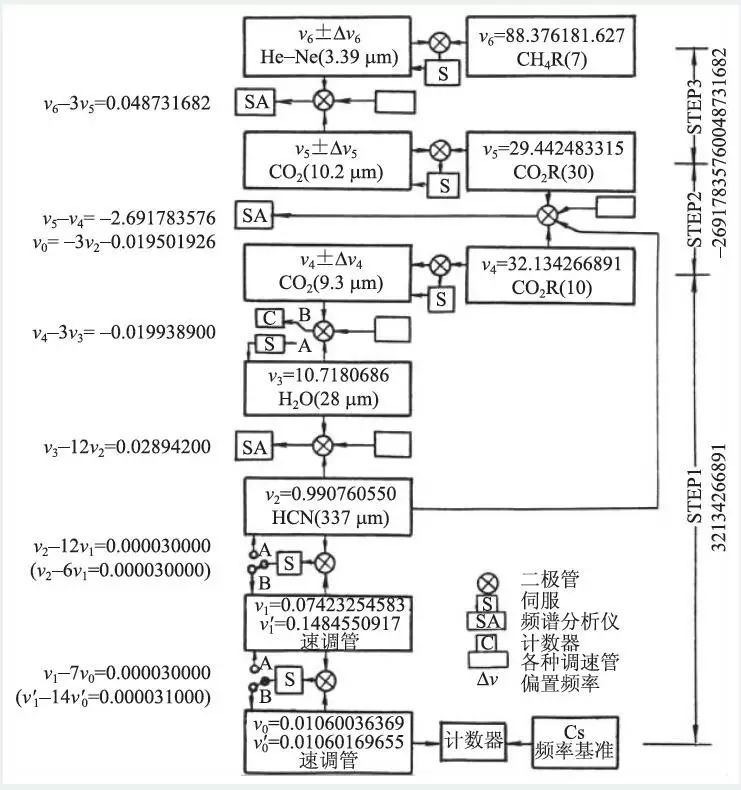
图7 美国NBS测量甲烷谱线的频率综合链(图中SA为频谱分析仪，用于检测拍频信号；S 为伺服装置，用于锁定频率信号；C为计数器，用于测量拍频信号的频率值；A，B代表附近方框内的频率信号)

1982 年，美国NBS又率先将绝对频率测量的上限扩展到可见光范围。这项测量实际上是以稳频CO₂ 激光器为起点，该激光的频率值是通过88 THz 的甲烷稳定激光进行测定的。首先测量520 THz(576 nm)¹²⁷I₂的17-1 带P(62)跃迁o 分量的频率值为

f =520206808547 kHz ， (4)

其不确定度为1.6×10^-10。

为了测量光频和波长标准中最实用的473 THz(633 nm)¹²⁷ I₂稳定的He-Ne激光器的绝对频率值，选择了四波混频方案，共采用了7台大型激光器才实现了这一目标。由此获得了目前真空中光速的测量值为299792457.4 ±0.1 m/s。

633 nm碘吸收的超精细结构i分量的频率测量的结果为

f =473612214830±74 kHz，

其不确定度与(4)式的520 THz碘谱线相同，为1.6×10^-10。

1992 年，法国激光器锁定在碘的11-5 带R(127)线的f 分量上的频率测量值为

f =473612353586.9 ± 5 kHz，

其测量不确定度为1×10^-11。但是，由于INM12 激光器的频率复现性大于这个数值，因此，CCDM将其频率不确定度规定为2.5×10^-11。

上述频率值与1983 年美国NBS 的测量值相比，其不确定度降低10 倍，而频率值减小了137 kHz，与美国NBS 的测量不确定度相比，减小了2倍的量级。

光速的测定在光学的研究历程中有着重要的意义。虽然从人们设法测量光速到人们测量出较为精确的光速共经历了三百多年的时间，但在这期间的每一点进步都促进了几何光学和物理光学的发展，尤其是在微粒说与波动说的争论中，光速的测定曾给这一场著名的科学争论提供了非常重要的依据。

激光作为频率标准或波长标准, 其准确度及其进一步提高的潜力均已超过了当时的⁸⁶Kr 长度基准的水平，因此正酝酿着采用什么方式来取而代之。在长达十年的讨论中，主要有两种不同的意见：

(1)选用一种准确度较高而又方便使用的激光波长标准代替⁸⁶Kr 光谱灯作为新的长度基准，更改米的定义。(2)时间和长度两个基本单位当时是分别独立定义的，前者用¹³³Cs 的跃迁频率作为秒单位的定义，后者用⁸⁶Kr 的橙黄谱线波长作为米单位的定义。用激光频率ν(用秒单位进行测量)和激光真空波长λ(用米单位进行测量)的乘积得到的真空中光速c(=νλ)是一个导出单位(速度单位)。多数科学家建议，由于真空中光速c 是基本物理常数，物理学上认为它是一个恒定不变的量，可以通过约定，将它的值采用一个国际公认的约定值，由此可推算真空波长λ=c/ν。由于光频标准频率值的不确定度可望逐步减小，直至到达或接近作为时间基准的铯频率基准的量级(10^-13—10^-14量级)，而真空波长测量由于受到光学元件等诸多条件的限制，很难超过10^-10量级。上述方式的定义，实质上是把长度单位通过以约定光速值从时间单位导出，使米定义的不确定度可进一步减小到10^-10量级以下。下面论述的米的重新定义就是按第二种意见具体确定的。

1983 年第17 届国际计量大会正式通过米的重新定义：“米是光在真空中1/299 792 458 秒的时间间隔内行程的长度”。

米的重新定义与1960 年的原定义相比有重大的变化。首先，在这个新定义中，把真空中光速c 的数值作为一个约定值299792458 m·s^-1，从而结束了物理学家们测量真空中光速长达300 年的历史。这是从物理量(或计量)单位制的定义角度，给光速测量结果划了句号。因为长度单位米和时间单位秒都是基本单位，原来两者是相互独立的，其间不存在依存关系。由这两个单位得到的光速值c=l/t=νλ，是一个导出的速度单位。随着科学技术的不断发展，c 的测量不确定度可以不断减小，从而使c 数值的位数也可以不断增加。但是，在具体实施上，若采用c=l/t 的方法，由于光速是一切速度的极限，它是一个很大的数值，形象地说，光在1 秒内的行程可环绕地球赤道7周半。在地球上用c=l/t 的方法，通过准确测量时间t，很难得到准确的c 值。在20 世纪，科学家们主要用c=νλ 的方法来准确地测量光速。用光频标准的频率值ν乘以真空波长值λ所得到c 值，其不确定度已达到了当时长度基准⁸⁶Kr 波长的极限4×10^-9，即使将来用激光波长来重新定义米，由于受到光学元件等的限制，波长测量不确定度的极限也不可能优于1×10^-10量级。在天文学测距中，用光年来表示的距离，其不确定度直接受c值不确定度的影响。1983 年的米定义，将光速确定为具有9 位数字的约定值，其不确定度为零，即c 值第9 位后的数字均表示为零。这在包括天文学及物理学其他领域的应用中，提供了极其准确的数值，也带来很大的便利；其次，用λ=c/ν来复现米定义时，其不确定度完全由频率ν决定；由于光频标准频率测量的不确定度可望不断减小，米定义的复现精度就能逐步提高；同时，也可以增加更有前途的新的频标作为新的推荐标准。综上所述，我们可以把这个更新后的定义视为一个开放性的定义。自1983 年米的重新定义以来的十多年历史已充分表明，这种开放性定义具有明显的优点。

由以上分析也可以看出新米定义复现方法的特点：其一，用l=ct 的方法，可简称为测时法，即根据光行进的时间来测距, 这种方法可在大地测量、军事测距或天文测量中应用；在实验室内复现米定义主要采用λ=c/ν的方法，可简称为测频法，即通过测量光频标准的频率来得到激光波长值，从而复现米定义；第三种方法是将研制的光频标准，在符合国际规定的条件下，采用国际计量委员会(CIPM)推荐的频率或波长值。第三种方法是第二种方法的派生结果，没有第二种方法准确测量所得出的推荐值，第三种方法便是无源之水，无本之木。

如上节所述，最早推荐作为激光波长标准的稳定激光的谱线，是1973 年第5 届CCDM推荐的3.39 μm甲烷吸收稳定的氦氖激光和633 nm 碘吸收稳定的氦氖激光的谱线； 1979 年， 第6 届CCDM又推荐了612 nm碘吸收稳定的氦氖激光的谱线，使推荐的激光波长标准增加到3 种，它们均为氦氖激光谱线；1982年，第7届CCDM又推荐了576 nm碘吸收稳定的染料激光的谱线和515 nm碘吸收稳定的氩离子激光的谱线作为新的频率和波长标准，使激光频率和波长标准的数量增加到5 种；1983 年，第17 届国际计量大会正式通过了长度单位米的重新定义，将上述5 种光频标准推荐作为复现米定义的谱线； 1992 年， 第8 届CCDM会议又增加推荐了3 种光频标准，它们分别是543 nm 和640 nm 碘吸收稳定的氦氖激光的谱线以及657 nm钙吸收稳定的染料激光谱线组成的光频标准，使光频标准的数量增加到8 种；1997 年9 月，第9 届CCDM会议又推荐了532 nm碘吸收稳定的Nd:YAG激光倍频的谱线，674 nm锶吸收的染料激光谱线，778 nm铷吸收的半导体激光谱线，10.3 μm OsO₄吸收稳定的二氧化碳激光谱线组成的光频标准，使复现米定义的光频标准数量增加到12 类之多。从20 世纪70 年代的3条谱线，80 年代5 条谱线，发展到90 年代的12 条谱线，本世纪更新为13 条谱线，可以看出光频标准不但数量增加，而且不确定度已逐渐趋近甚至超过作为时间频率基准的铯原子钟的迅速发展趋势。

其次，20 世纪70 年代和80 年代所研究的光频标准主要以氦氖激光和染料激光为主体，而90年代的研究则以固体激光和半导体激光为主体，近年来则以激光冷却的囚禁离子等参考频率为主体。由于后者在一系列性能上均优于前者，使光频标准在频率稳定度和复现性等技术指标方面有很大的提高。几年前，由于尚受到激光频率测量方法及其不确定度的限制，有些频标的频率值的不确定度远大于其频率复现性的数值。近年来，由于飞秒锁模激光的光梳测频技术的发展，使光频标准充分展示了它的巨大潜力。2003 年国际计量委员会推荐的13 种光频标准的有关参数，包括其频率值及不确定度见文献。