点击蓝色“
五分钟学算法
”关注我哟
加个“
星标
”,天天中午 12:15,一起学算法

作者 | 李威
来源 | 五分钟学算法
今天分享的题目来源于 LeetCode 第 23 号问题:合并 K 个排序链表。本文采取两种思路进行分析。
题目描述
合并
k
个排序链表,返回合并后的排序链表。请分析和描述算法的复杂度。
示例:
输入:
[
1->4->5,
1->3->4,
2->6
]
输出: 1->1->2->3->4->4->5->6
题目解析
方法一:贪心算法、优先队列
思路分析:
1、由于是 𝑘 个排序链表,那么这 𝑘 个排序的链表
头结点
中
val
最小
的结点就是合并以后的链表中最小的结点;
2、最小结点所在的链表的头结点就要更新了,更新成最小结点的下一个结点(如果有的话),此时还是这 𝑘 个链表,这 𝑘k 个排序的链表
头结点
中
val
最小
的结点就是合并以后的链表中第 2 小的结点。
写到这里,我想你应该差不多明白了,我们每一次都从这 𝑘 个排序的链表
头结点
中拿出
val
最小的结点“穿针引线”成新的链表,这个链表就是题目要求的“合并后的排序链表”。
“局部最优,全局就最优”,这不就是贪心算法的思想吗。
这里我们举生活中的例子来理解这个思路。
假设你是一名体育老师,有 3 个班的学生,他们已经按照身高从矮到高排好成了 3 列纵队,现在要把这 3 个班的学生也按照身高从矮到高排列 1 列纵队。我们可以这么做:
1、让 3 个班的学生按列站在你的面前,这时你能看到站在队首的学生的全身;
2、每一次队首的 3 名同学,请最矮的同学出列到“队伍 4”(即我们最终认为排好序的队列),出列的这一列的后面的所有同学都向前走一步(其实走不走都行,只要你能比较出站在你面前的 3 位在队首的同学同学的高矮即可);
3、重复第 2 步,直到 3 个班的同学全部出列完毕。
具体实现的时候,“每一次队首的 3 名同学,请最矮的同学出列”这件事情可以交给
优先队列
(最小堆、最小索引堆均可)去完成。在连续的两次出队之间完成“穿针引线”的工作。
下面的图解释了上面的思路。
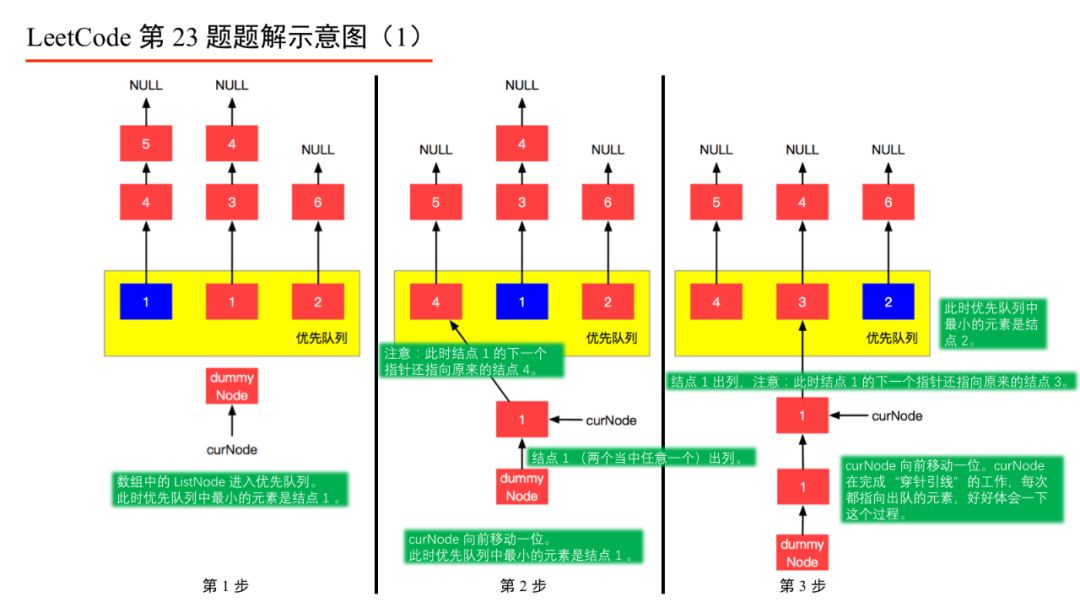
LeetCode 第 23 题:合并K个排序链表-1

LeetCode 第 23 题:合并K个排序链表-2
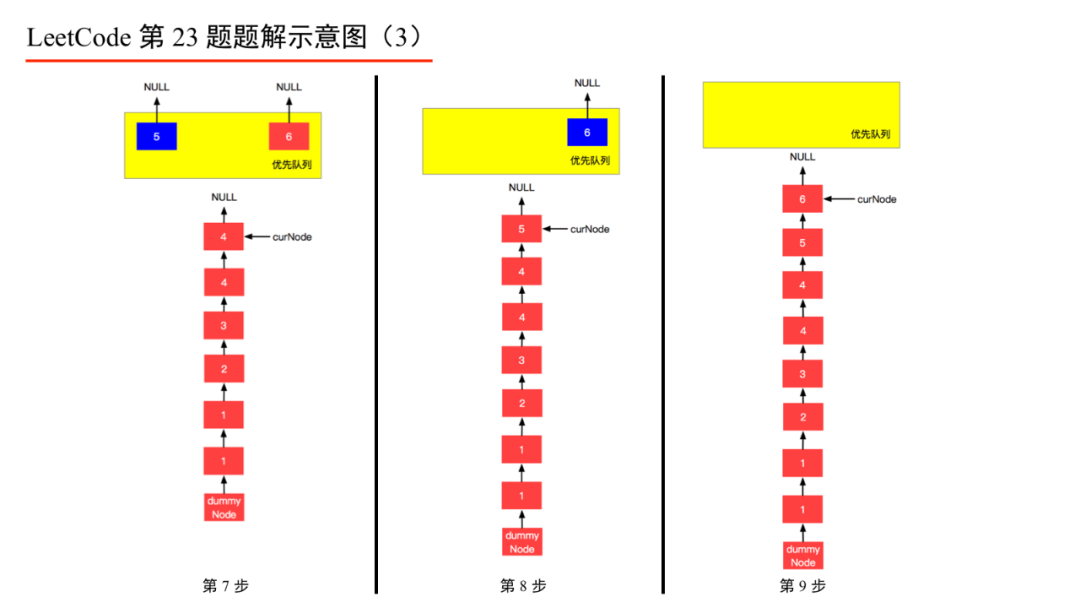
LeetCode 第 23 题:合并K个排序链表-3
代码实现
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
int len = lists.length;
if (len == 0) {
return null;
}
PriorityQueue priorityQueue = new PriorityQueue<>(len, Comparator.comparingInt(a -> a.val));
ListNode dummyNode = new ListNode(-1);
ListNode curNode = dummyNode;
for (ListNode list : lists) {
if (list != null) {
priorityQueue.add(list);
}
}
while (!priorityQueue.isEmpty()) {
ListNode node = priorityQueue.poll();
curNode.next = node;
curNode = curNode.next;
if (curNode.next != null) {
priorityQueue.add(curNode.next);
}
}
return dummyNode.next;
}
}
复杂度分析
方法二:分治法
如果我们不想“穿针引线”,那么“递归”、“分治”是一个不错的选择。
代码结构和“归并排序”可以说是同出一辙:
1、先一分为二,分别“递归地”解决了与原问题同结构,但规模更小的两个子问题;
2、再考虑如何合并,这个合并的过程也是一个递归方法。
代码实现
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
int len = lists.length;
if (len == 0) {
return null;
}
return mergeKLists(lists, 0, len - 1);
}
public ListNode mergeKLists(ListNode[] lists, int l, int r) {
if














