Nat. Phys.: 蜂窝状范德瓦尔斯磁体中从三维反铁磁态到二维残余向列态的维度转变

【研究背景】

残余序是由自发对称破缺相的主要序（ η ）部分熔化引起的。与不破坏其宿主晶格对称性的常规短程序不同，残余序对应于一个复合序（ η ^† τη，η 的二次形式，其中 τ 为矩阵），并打破主要序所破坏的对称性的一个子集。波动和无序通常是破坏主要序，并可能引入残余序的原因。温度的升高会导致热波动，而降低维度也可以独立地导致波动增强。在长程主要有序区域I（ ⟨ η ⟩ ≠0且 ⟨ η ^† τη ⟩ ≠0）和完全无序区域III（ ⟨ η ⟩ =0且 ⟨ η ^† τη =0）之间，可能存在残余有序情况的区域II（ ⟨ η ⟩ =0但 ⟨ η ^† τη ⟩ ≠0）。引入残余序的影响是深远的，因为它导致了许多量子材料系统丰富相图中相邻相的交织性质，包括铜基高温超导体、铁基超导体、电荷密度波系统等。在许多系统中，主要序与残余序的理论例子很常见：电荷或自旋密度波与向列性，配对密度波与charge -4e 超导性或向列性或电荷密度波，超导性与charge -4e 超导性或向列性，甚至从Z ₂ × Z ₂ 拓扑序量子自旋液体到Z ₂ 拓扑序量子自旋液体的任意子凝聚等。

残余序的实验表现主要集中在破坏旋转对称性但保留晶格平移对称性的向列性上。这种对称性要求使得四方和六方系统能够支持向列性的出现。实际上，在铜酸盐和铁基等四方系统中，Z ₂ Ising向列性可以从电荷和自旋涨落中发展，它将四方四重对称性破坏为正交双重旋转对称性，同时保留平移对称性。相比之下，在六方系统中预期会出现Z ₃ Potts向列性。这种向列性破坏六方六重（或三重）旋转对称性，同时保留平移对称性。最近，在体相Fe _1/3 NbS ₂ 和体相FePS ₃ 等系统中，在其长程有序磁相中观察到了Potts向列性的特征。然而，没有主序的本征Potts向列序的研究还较少。预期Z ₂ Ising向列性和Z ₃ Potts向列性在施加外部应变时也会表现出不同的相变行为。

降低维度是增强涨落的一个有前景，但研究较少的途径。事实上，向列性的开创性理论研究常常使用二维模型。在这方面，本文选择了具有XY型自旋各向异性的2D蜂窝状磁性系统NiPS ₃ ，以获得更强的自旋涨落来实现Z ₃ Potts向列性。这项研究与主流的2D磁性研究不同。

单层NiPS ₃ 具有D3d三角晶体点群，具有面外三重旋转轴。由于相邻层沿a轴的横向移动，体相和少层NiPS ₃ 遵循单斜结构点群C2h。体相NiPS ₃ 在T _N,3D = 155 K下发生反铁磁（AFM）相变。在长程有序AFM态中，Ni ²⁺ 自旋沿a轴在zigzag链内铁磁对齐，而在相邻链之间反铁磁耦合。这种NiPS ₃ 中的长程zigzag AFM序自发破坏了单层的三重旋转对称性，同时以波矢 Q = k _M 破坏了平移对称性，其中 k _M 是布里渊区（BZ）M点的动量。预期存在三个简并的zigzag AFM态，它们的 Q 相互旋转120°, 即 Q j（j = 1, 2或3）。NiPS ₃ 体相中这种破坏旋转对称性（BRS）和破坏平移对称性（BTS）的AFM相具有非零主序参数 η _j ( r ) = ( S ( r ) − S ( r + e _j )) e ^{i Qj ⋅ r} . 其中 e _j 是平行于相邻自旋位点间 Q _j 的矢量， S ( r )是位点 r 处的自旋。由于XY模型中的弱各向异性、2D中的强自旋涨落以及铁磁-AFM交换竞争，预期少层NiPS ₃ 将实现区域II的情况，即具有BRS但无BTS的向列相，然后进入完全自旋无序的顺磁相，即区域III。

【成果介绍】

鉴于此，美国密歇根大学Liuyan Zhao教授团队与德克萨斯理工大学的Rui He教授团队合作，在Nature Physics期刊上发表了题为"Dimensionality crossover to a two-dimensional vestigial nematic state from a three-dimensional antiferromagnet in a honeycomb van der Waals magnet"的研究论文。该研究通过自旋弛豫测量和光学光谱学实验，观察到随着NiPS ₃ 层数减少，在吉赫兹到太赫兹频率范围内的自旋涨落显著增强。作者们利用蒙特卡罗模拟验证了实验中观察到的三重旋转对称性破缺现象。值得注意的是，在薄层NiPS ₃ 中，尽管旋转对称性被破坏，平移对称性却得以保持。这一发现表明，强量子涨落可能在破坏常规长程磁序的同时，稳定了一种新的非常规磁性态。这项研究为理解低维材料中的量子涨落效应及其对磁性相变的影响提供了重要的实验证据和理论支持。

【图文导读】

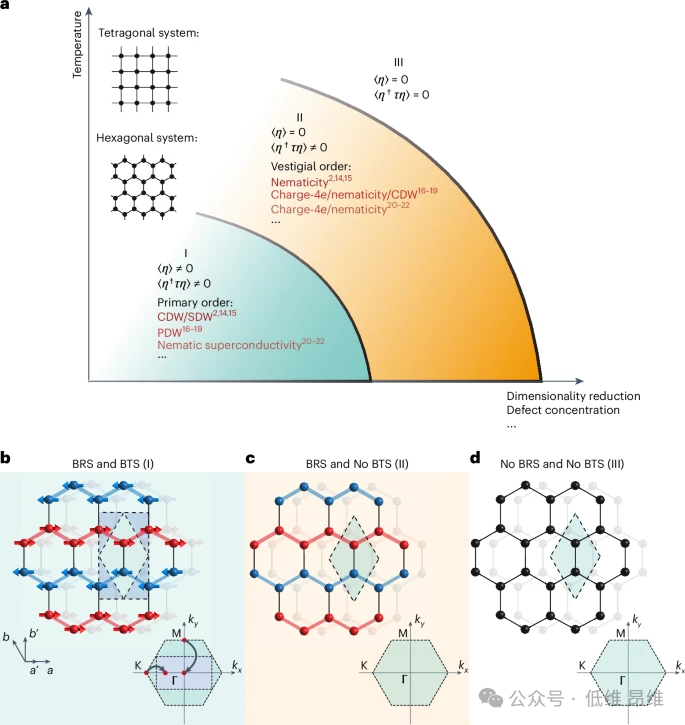
图1： NiPS ₃ 中残余序和磁态的示意相图。a. 示意相图展示了主序（ η ）和残余序（ η ^† τη ）作为温度（纵轴）和其他独立因素（如降低维度或引入无序导致的增强涨落，横轴）的函数。b. 3D NiPS ₃ 中具有破坏旋转对称性（BRS）和破坏平移对称性（BTS）的长程zigzag形反铁磁（AFM）序的示意图。c. 2D NiPS ₃ 中具有BRS但无BTS的自旋诱导向列态的示意图，对应于a中的区域II。d. NiPS ₃ 中无BRS和BTS的自旋无序态的示意图。

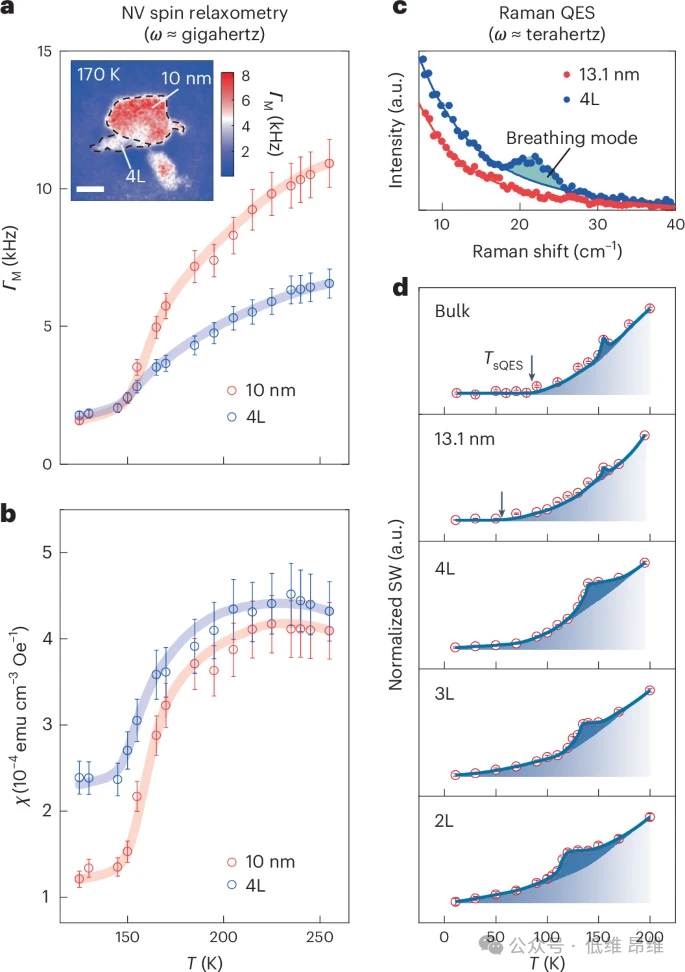
图2： 通过NV弛豫测量和拉曼光谱测量的少层NiPS ₃ 中厚度依赖的自旋涨落。a. 10 nm和4层（4L）NiPS ₃ 下方NV中心测得的NV自旋弛豫率 Γ _M 的温度依赖性。b. 10 nm和4L NiPS ₃ 的拟合磁化率 χ 随温度的变化。c. 在170 K下，使用波长 λ = 532 nm测量的13.1 nm和4L NiPS ₃ 的归一化准弹性散射（QES）拉曼光谱。d. 不同厚度NiPS ₃ 在8–40 cm ^-1 范围内的QES积分强度随温度的变化。

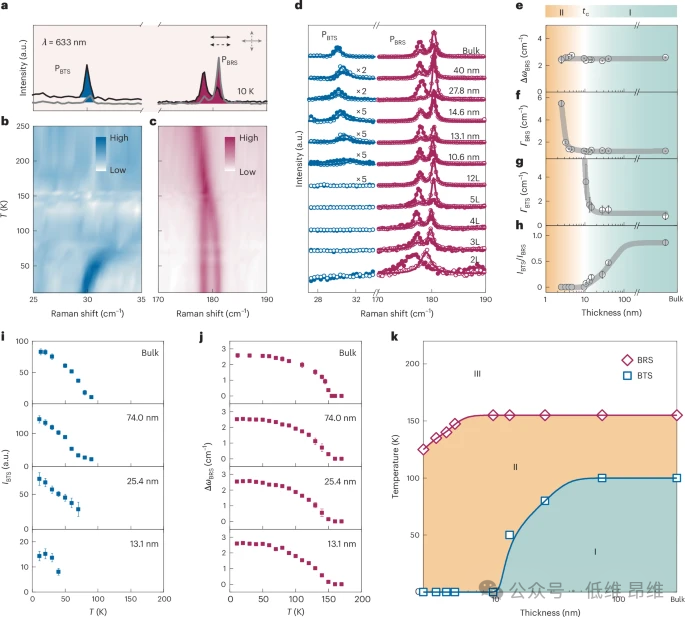
图3： 拉曼光谱中破坏平移对称性（BTS）和破坏旋转对称性（BRS）特征的厚度依赖性。a. 在10 K下使用波长 λ = 633 nm在平行（黑色曲线）和交叉（灰色曲线）通道测量的体相NiPS ₃ 的线偏振拉曼光谱。b. 体相NiPS ₃ 平行通道中PBTS模式的温度依赖拉曼光谱。c. 体相NiPS ₃ 平行通道中PBRS模式的温度依赖拉曼光谱。d. 在T = 10 K时不同层数NiPS ₃ 在平行（实心圆）和交叉（空心圆）通道的拉曼光谱。e. T = 10 K时PBRS拟合频率分离 Δω _BRS = ω _BRS-h – ω _BRS-1 的厚度依赖性。f. T = 10 K时PBRS拟合线宽 Γ _BRS 的厚度依赖性。g. T = 10 K时PBTS拟合线宽 Γ _BRS 的厚度依赖性。h. T = 10 K时拟合强度比 I _BTS / I _BRS 的厚度依赖性。i. 不同厚度NiPS ₃ 的P _BTS 模式的温度依赖性。j. 不同厚度NiPS ₃ 的P _BTS 模式的温度依赖性。k. NiPS ₃ 的厚度-温度相图。

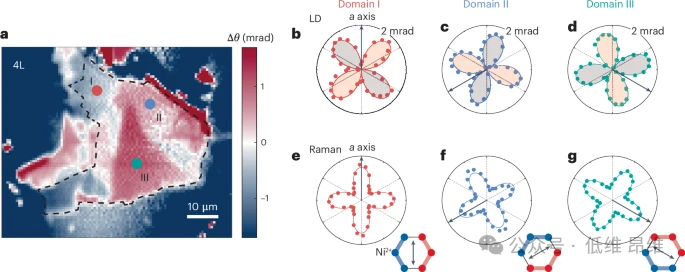
图 4：4层（4L）NiPS ₃ 的偏振依赖线性二色性（LD）和拉曼数据。a. 4L NiPS ₃ 的空间分辨LD图。b-d. 图a中所示4L NiPS ₃ 样品中向列畴I（b）、II（c）和III（d）的角度依赖偏振旋转Δ θ 。e – g. 图a中所示4L NiPS ₃ 样品中相应Potts向列畴I（e）、II（f）和III（g）在T = 10 K时拟合的P _BRS-l 强度的偏振依赖性极坐标图。

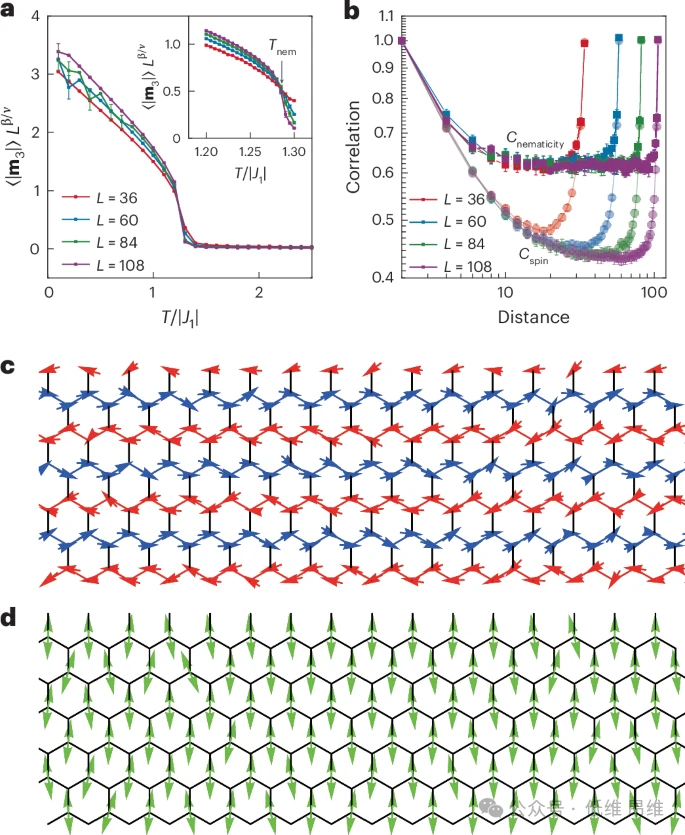
图 5： 双层（2L）NiPS ₃ 中磁态的蒙特卡罗计算。a. 四种不同系统尺寸（L = 36、60、84和108）下标度化Potts向列序参数（ m