作者:Stephen Woodcock
翻译:山寺小沙弥
审校:yangfz
数学是帮助我们理解一些模型的有用工具。然而,当我们凭直觉去解释这些模型的时候,往往会出现一些错误。在本文中,我们将介绍我们常犯的一些错误,以及如何在考虑统计数据,概率和风险时避免这些错误的出现。
生活中你经常会看到一些新闻或者文章,它们宣称某种事物或者某种行为,可以使人们活得更加健康,抑或者危害我们的身体,也许有的还宣称利弊皆有。为什么看似严谨的科学研究能产生相反的结论呢?
现如今,研究人员可以通过一些软件随时地分析数据并输出复杂的统计测试结果。虽然这些软件的功能很强大,但是它们同时也为那些对统计知识知之甚少的人打开了误解之门,他们往往会不能正确理解数据之间的微妙关系,并得出错误的结论。
以下是常见的谬误和悖论,我们将进行详细的解释,剖析它们是如何蒙蔽我们的双眼从而得出错误的结论的。
将不同组别的数据合并时,会导致各组原本表现出来的某种规律消失,当这种情况发生时,合并之后呈现出的新规律甚至可能与每组的原本的规律相反。
举个例子,某种治疗手段在不同的组别里对患者的身体恢复是有害的,但是将所有组别的数据合并起来看,我们却会发现它竟然对患者身体的恢复是有帮助的。
当组成各组的成分差别较大的时候,就可能出现上述现象。如,对病人的数量进行筛选,使得两组试验中病人的组成差别很大(老人、小孩、成人的比例有很大的差别)时,将数据简单的合并之后就会得出这样的结论:有害的治疗变成了有益的治疗。
假设有一个双盲试验(在双盲试验中,受试验的对象及研究人员并不知道哪些对象属于对照组,哪些属于实验组),将患者分成两组,每组有120人,但是两组中患者的年龄结构有很大的差异(第一组分为10人、20人、30人、60人,第二组分为60人、30人、20人、10人)。第一组的患者将接受治疗,而第二组的患者不进行治疗。
总体结果表明,治疗对患者是有益的,接受治疗的患者的身体恢复率大于没有接受治疗的患者。
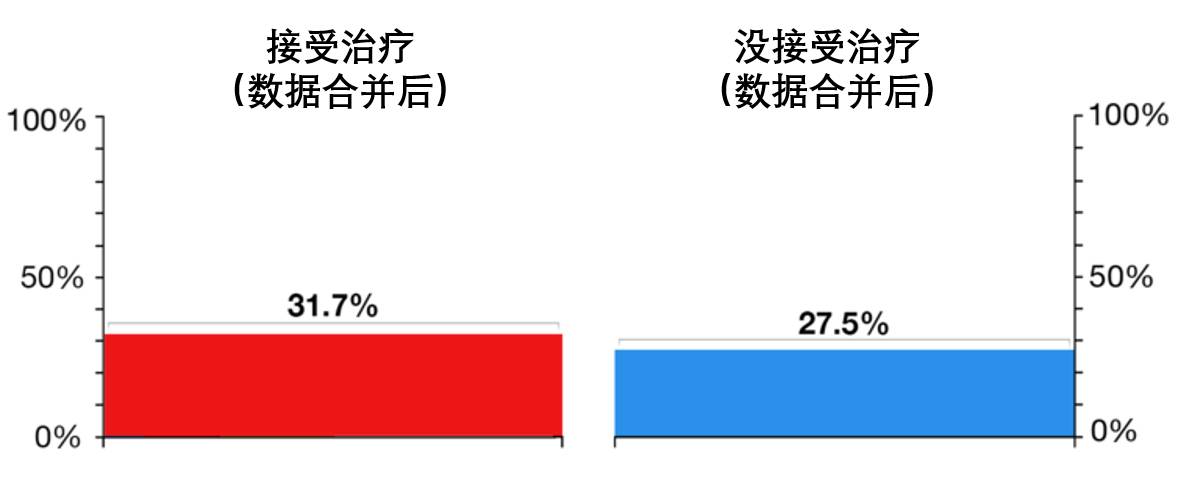
然而,当你深入研究两组中各个患者群体时,你会发现在所有的患者群体中, 没有接受治疗的患者身体恢复率提高了。
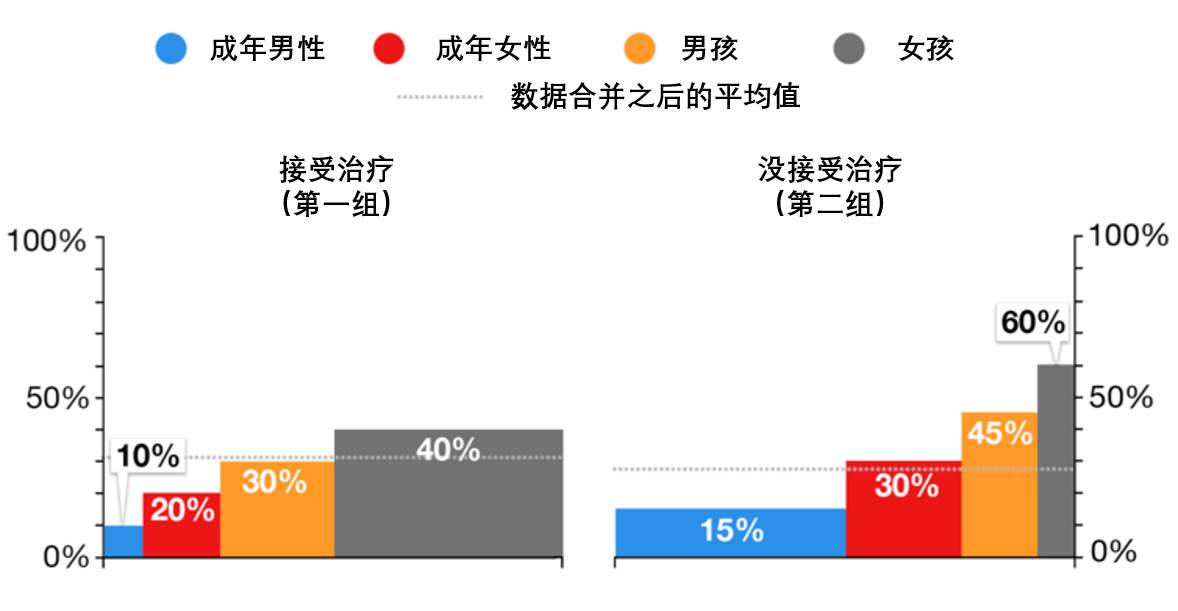
我们注意到,每组中不同年龄的患者人数是不同的,甚至是差别很大的,这就是我们得出错误结果的原因。在这种情况下, 如果简单的将两组数据合并,就容易得出错误的结论。
当我们判断某个事件发生的可能性时,如果我们忽略了重要信息,就会产生误判。
例如,假如有一个人说他很喜欢音乐,我们可能认为他是一个音乐家,不会考虑他也许是个会计师。然而,现实中,会计师的人数远大于音乐家的人数。我们太容易被一些条件影响(这个例子中的“喜欢音乐”),忽略基本比例,从而得出错误的结论(这个例子中的“他是一个音乐家”)。
基本比例谬误常常发生在当一个选项的基数远大于另一个选项的基数时。
假如有一种罕见疾病,患者在人群中只占4%。
此时有一种针对这种疾病的测试方法,但是它并不是很完美。如果有个人患有该疾病,但是这种测试方法只会告诉我们这个人的患病几率为92%(也就是100个患者中,只有92个是诊断正确的)。如果这个人是健康的,那么该测试方法会告诉我们他有75%的健康几率(也就说100健康的人中,只有75个是诊断正确的)。
如果我们对一个群体进行测试,发现有1/4的人患病,我们可能会想,这些人也许真的病了。然而,事实并不是这样。

根据我们的条件,在4%的患有该疾病的人群中,有92%的人可以被确诊为患病(即总人口的3.68%)。但在另外的96%的群体中,25%的人被误诊为患病(占总人口的24%)。
也就是说,被诊断为患有该病的27.68%的人群中,实际患病的几率只有3.68%。所以说,对于被诊断为患病的人来说,实际上真正患病的人只占13.29%。
令人担忧的是,世界上就有这样的例子存在
。在一项著名的研究中,医生被要求进行类似的计算, 通过乳腺的X光图像告知某人是否患病, 只有15% 的正确率。
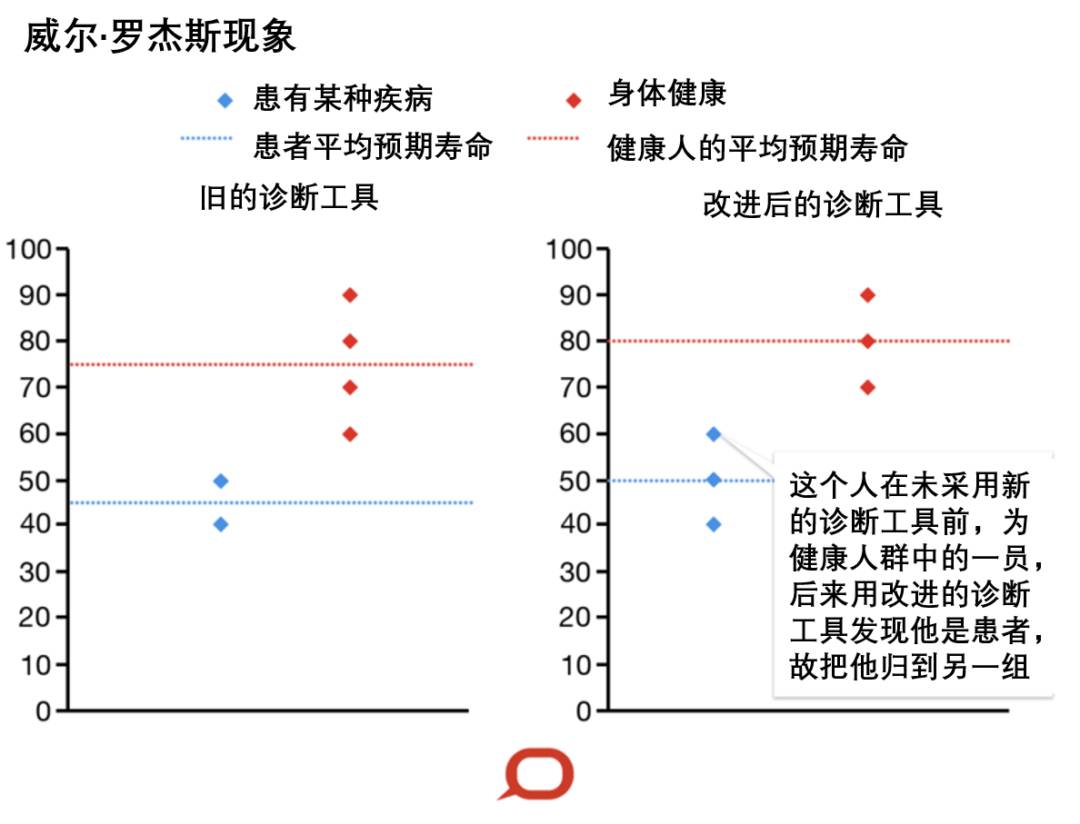
将某集合中的元素移到另一集合后,两个集合的平均值都提高了,这就是威尔·罗杰斯悖论。
这个现象的名字来源于美国喜剧演员威尔·罗杰斯(Will Rogers),他曾开玩笑地说:“那些从俄克拉何马州搬到加利福尼亚州的人,提高了两个州的平均智商。”
当数据从一个集合重新分类到另一个集合时, 如果该数据低于它要离开的集合的平均值, 但高于它所加入的集合的平均值, 则两个集合的平均值将会增加。
假设有6个人,医生估计他们的预期寿命分别是40岁、50岁、60岁、70岁、80岁、90岁。
预期寿命为40岁和50岁的人已被诊断患有某种疾病; 其他四个没有。患者的平均寿命为45岁,另外四个的平均寿命为75岁。
如果开发出一种改进的诊断工具来检测那个预期寿命为60岁的人,并且发现他患有和那两个人一样的疾病,那么此时我们就要把他归到另一组,这时我们会发现,两组的平均预期寿命均提高了5岁。
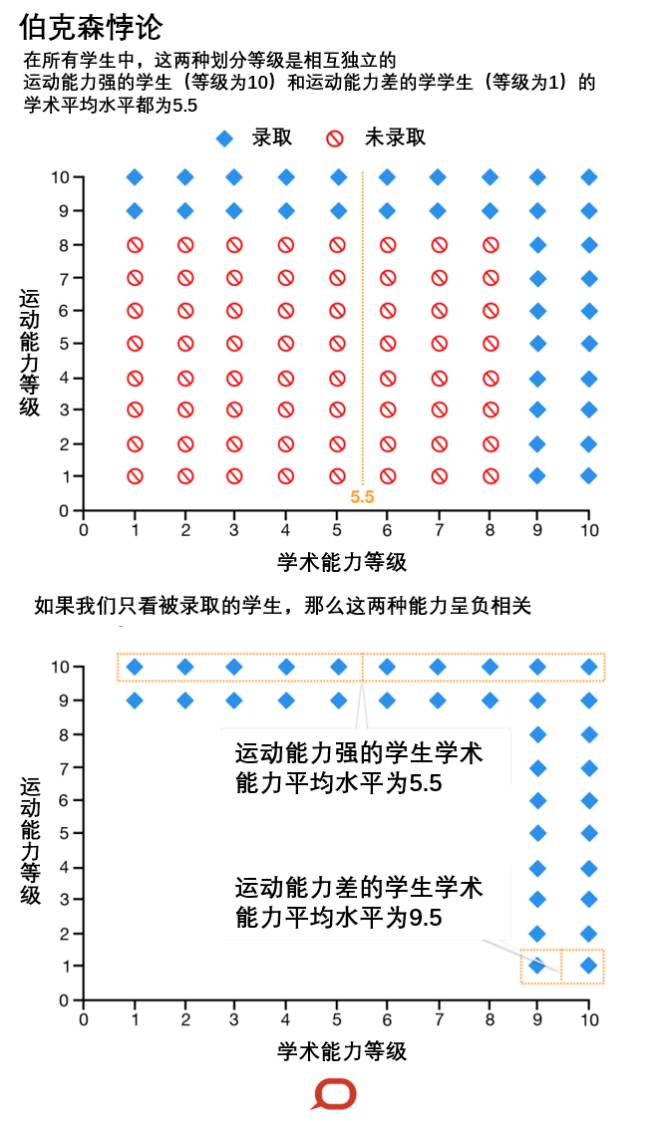
伯克森悖论指的是对于两个独立的事件,认知者误以为这两个事件具有某种相关性。
这样的悖论通常发生在两个相互独立的集合中,相互独立意味着两个集合之间没有任何联系。但是如果我们只看两个集合中的某个子集,那么此时也许这两个子集中的元素是负相关的。
当子集不是整个种群的无偏样本时, 就会发生这种情况
,医学统计中经常引用伯克森悖论。例如,假设有一个医院,它只治
疗a疾病和b疾病,或者两个疾病均可以治疗,那么尽管这两种疾病是相互独立的,但是这种医院容易使我们觉得a疾病和b疾病是有关联的。
考虑一个以学术能力和运动能力为基础招收学生的学校。假设这两种技能是完全独立的。也就是说,在所有的学生中, 一个运动能力强的学生和一个运动能力弱的学生,都有可能具有优秀的学术能力或者差的学术能力。
但是,如果这个学校只招收技能优秀的学生(两种技能均优秀或者其中一种优秀),那么在这群被录取的学生中,体育能力和学术能力呈负相关。
为了说明这点,将所有学生(不止是这个学校的学生)按照两种技能强弱分别从1到10划分等级,每种技能的在每个等级里都有相同比例的人。
假设该学校只招收其中一个技能的等级或者两个技能的等级为9或者10的学生。
此时我们看看被录取的学生,运动能力强的学生和运动能力差的学生的平均学术等级都是相等的,都为5.5。然而, 高水平运动员的学术能力平均等级仍然和整个学生群体的学术能力平均等级一样(均为5.5),但运动能力差的学生的学术能力平均等级是9.5,此时我们会发现,这两个能力呈负相关。
对于具有很多变量的数据,如果在随机试验中出现某种无法预料的趋势,那么此时就容易出现多重比较谬误。
当在许多变量之间寻找变量之间的某种联系时,如果变量很多,我们就很容易忽略一些可能性。比如,有1000相互独立的变量,两两组合的话,就存在499500种可能,那么在这些组合中,也许存在一些巧合,使得它们似乎是相关的。
即使它们两两之间是独立的,但是对于那么多的可能性,总有一些数据巧合,使得某两个变量之间似乎存在某种联系。
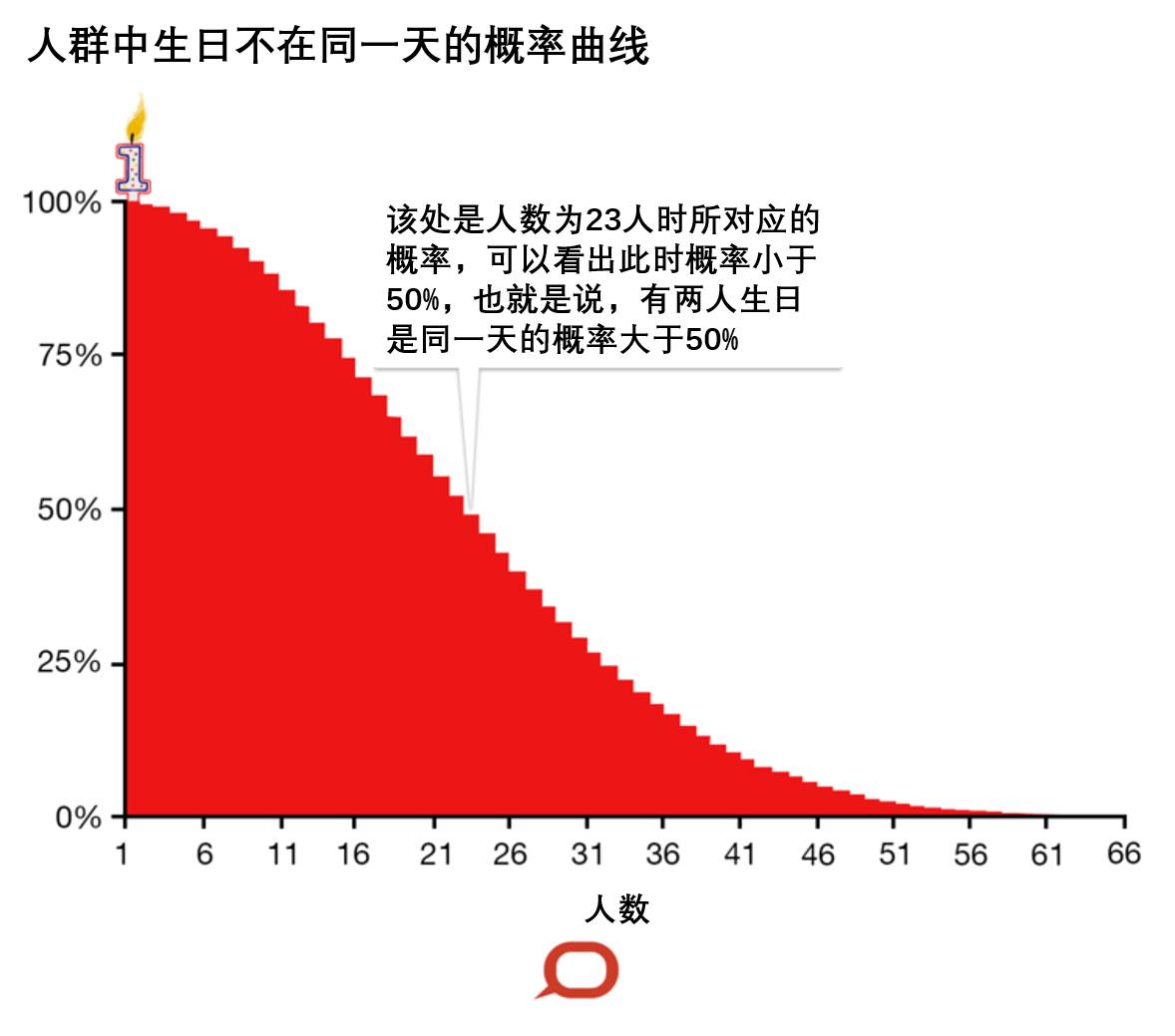
生日悖论就是一个多重比较谬误的典型例子。
假如有23个人,如果要计算有两个人在同一日出生的概率,在不考虑特殊因素的前提下,例如闰年、双胞胎,假设一年365日出生概率是平均分布的(现实生活中,出生概率不是平均分布的),那么这些人中,有两个人生日是同一天的概率大于50%。
这样的结果挺让人难以置信的,因为人们很少遇到和自己生日相同的人,当然,如果随机选两个人,那么他们生日是同一天的概率是非常低的(小于0.3%)。
对于这23个人,两两组合,能产生253种可能性,在这么多的可能性中,是可能出现生日相同的组合的,而且概率很高。有兴趣的读者可以算一下,最终的结果可以用一个公式表达出来:
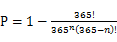
其中P为概率,n为人数,如果计算23人,将23带入即可,算出来约为50.7%。
所以对于40个人来说,其中两个人生日相同的概率将近90%。
原文链接:
https://theconversation.com/paradoxes-of-probability-and-other-statistical-strangeness-74440



