在
《...（一）》
中，小夕从映射的角度讲解了矩阵及矩阵运算，这也是机器学习中看待矩阵的非常重要的视角。
另一方面说，矩阵当然也是用于存储数据的数据结构，这也是最好理解的形式。另外还可以看做是一个线性方程组（课本上讲烂了的开头），甚至可以将其仅仅看做一般化的张量（tensor）中的一个普通切片（slice），或者说其中一层。所以矩阵代表什么含义，要在不同的场景中灵活对待，不要局限在一种视角哦。
继续从映射的视角来看。
小夕说，不同的矩阵就代表着不同的映射，就像上一篇文章讲的，
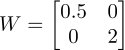就可以表示“将输入的空间的第一个维度的坐标轴缩短为原来的一半，将第二个维度的坐标轴拉伸为原来的两倍”。这就是这个矩阵的含义。
例如，输入一个
二维空间
里的多个样本点：
比如
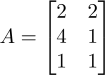
此时的矩阵就是
存储数据的视角
啦。这里的矩阵就是每一行就是空间中的一个样本点，所以这个矩阵就代表
二维空间
里的
3个样本点
。
所以将A中这个空间的三个样本丢给W这个映射，就得到了三个样本在新的空间的镜像点（跟高一时学的集合的映射是一个概念）：
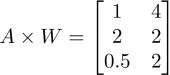
看，是不是新得到的三个样本的第一维都被压缩成了原来的一半，而第二维被拉伸成了原来的两倍呢~
而神经网络中，每一层的输出经过权重矩阵，映射到下一层的输入的过程，就是上述这个过程哦（没有理解的再看看这篇文章
《神经网络激活函数》
）
好啦。从映射的视角接着走。那么既然矩阵是描述映射的，那么肯定会有更严谨，更直观的形式去描述一个矩阵背后所暗示的映射规则。
这个更直观的形式是什么呢？
好，然后我们将映射
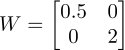更加夸张一下，我们来看映射
。
显然，按照小夕之前的讲解，这个映射就代表将第一维度压缩为原来的0.99倍（几乎没有变化！），将第二维度拉伸为原来的100倍（显然变化十分极其非常的大）。这个映射的
作用对象
很明显：
1
、
第一维度坐标轴
。怎么描述这个作用对象呢？回顾一下中学数学，在二维空间中，第一维度坐标轴不就是(x,0)嘛~既然是描述坐标轴，我们不妨用一个单位为1的向量表示x轴，即(1,0).
2
、
第二维度坐标轴
。同样的道理，在二维空间中，第二维度坐标轴就是y轴，表示为(0,1)
这个映射
对每个作用对象的作用程度
也很明显不一样：
1
、对第一维度坐标轴的作用程度就很小，对它几乎没有改变（改变成了原来的0.99倍），所以我们直接用0.99来表示作用程度（显然，越接近1表示作用程度越小）。
2
、同样，这个映射对第二维度的坐标轴作用程度非常大。所以用100来表示。
好啦~小夕用“作用对象”和“对某作用对象的作用程度”是不是就已经非常清晰的描述清楚了矩阵
的映射规则呢~所以理论上说，这两者应该完全等价才对~
学过线代的你有没有灵光一现呢~
没！错！
小夕这里讲的
“作用对象”
就是大学课本讲成一坨的
“特征向量”
(eigenvector)
！小夕这里讲的
“对某作用对象的作用程度”
就是课本里的
“特征值”
(eigenvalue)
！因此，一个矩阵，或者说一个线性映射，完全可以用它的全部特征向量及其对应的特征值去描述！（当然严谨的说是
方阵
，先接着开车，下一篇文章再解释细节）
而将矩阵分解为它的特征值与特征向量的过程被称为
“
特征分解”
（Eigendecomposition）
，又称
"
谱分解"
（Spectral decomposition）
。特征分解是众多矩阵分解中的一种，因此当然原矩阵A会被分解成几个目标矩阵啦~这里的目标矩阵当然就是两个，一个由特征向量组成的，还有一个是由特征值组成的。
你可以试一下，将上面的两个特征向量叠在一起（一列为一个特征向量）：
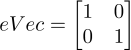
然后每个特征向量
对应的
特征值
依次
放到一个
对角矩阵
的各位置上
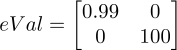
然后由公式
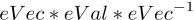即可以恢复出原映射W。（注:
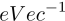是eVec的逆矩阵）
对于这个例子，一眼就能算出来肯定是对的~对于
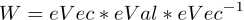的证明，可以参考各种教材和博客，就不展开啦。（文章末尾有链接推荐）
有了对特征值和特征向量的这一层理解，我们当然很容易继续联想到：
当一个矩阵的特征值中包含
0
时，就表示要将一个“坐标轴”直接毁灭！（将一个坐标轴映射回原点。这个“坐标轴”就是这个0特征值所对应的特征向量(所描述的方向)）；
同理，
负数
特征值就表示将它所对应的特征向量所在的坐标轴反转。因此，-1就表示将该坐标轴反转，但是不拉伸也不压缩。(-1,0)表示反转且压缩，(-∞,-1)表示反转且拉伸。
