一个价值“十万亿”的公式

牛顿 曾经 说过：我可以计算天体运行的轨迹，却没有办法计算人性的疯狂。

据说牛顿买了当初大家都非常看好的 英国 南海公司股票，但最终由于南海泡沫破灭， 官至皇家造币局局长的 牛顿巨亏了 2万英镑，为此 他才 发出这番感慨。

不过， 20世纪的布莱克和斯克尔斯 却似乎有自己的不同意见： 经济没有那么复杂，关键是数学关心不关心而已。

这两位玩转风云的金融大师，在 1973年 对 1966年至1969年 间 期权交易数据 进行 分析 后发表《期权定价和公司债务》一文，给出了期权定价公式， 一个堪称金融巫师的公式。

为表纪念，这个公式以二人名字命名， 即 著名的布莱克 -斯科尔斯公式。

这个公式向世界证明， 无论 经济的表面现象有 多复杂， 数学总能将这种 复杂刻画出来。

后来，斯科尔斯和默顿又进一步 发展 了这一方程 ， 为包括股票、债券、货币、商品在内的新兴衍生金融市场的各种 以市价价格变动定价 的衍生金融工具 的合理定价奠定了基础。

这个方程 的崛起 助力全球金融衍生市场步入全盛时期 ，一个衍生工具的时代冉冉升起。它创造出数十万亿金融衍生产品，并令美国金融行业升至社会所有行业的顶峰，甚至包括世界经济也因衍生市场的繁荣而焕然一新。

美国 “第二次华尔街革命”也由此吹起了新生的号角，“金融工程”在经济学界破土而出， 人称 “数量分析专家”的新一代交易家 成为华尔街最炽手可热的精英人才。

大批固步自封的传统投资银行在这个过程中猝不及防地转瞬江河日下，而一家长期资本管理公司 —— LTCM (Long-Term Capital Management ） 却开始展露锋芒。

关于布莱克—斯科尔斯方程的伟大应用，LTCM是最有发言权的，可以说，它是这一方程的最佳代言人。通过一丝不苟地执行布莱克—斯科尔斯方程套期理论， 在整个金融界掀起一翻腥风血雨，让整个华尔街都闻风丧胆，而后却又因此骤然一落千丈，沦为史上最大对冲基金失败案例 。

至今回想起那段岁月，人们仍难免心有余悸。

1994年，长期资本管理公司LTCM创立，这是一家主要 从事定息债务工具套利活动 的对冲基金公司。自一出生，就是天子骄子。

LTCM的创始人是被誉为能“点石成金”的华尔街“债券套利之父”梅里韦瑟，早期曾就职于华尔街的著名投资银行所罗门兄弟公司债券部门，离开后创立了LTCM。合伙人包括前美联储副主席莫林斯、默顿和斯科尔斯等。其中斯科尔斯和默顿两位泰斗级大师， 前者是布莱克—斯科尔斯方程的两位创始者之一，后者是公式的改进人 ，他们因此获得了1997年的诺贝尔经济学奖。而彼时，方程的另一创立者布莱克，因逝世遗憾与奖项无缘。

这样一支号称“每平方英寸智商密度高于地球上任何其他地方”的梦之队，共集结数学、金融、政客、交易员等诸多精英于一体， 在成立之初就毫不费力地融资了12.5亿美元。

与传统债券交易员依赖经验和直觉不同的是，梅里韦瑟更相信数学天才的头脑和计算机里的模型， 他认为数学模型是揭露债券市场秘密的最好利器 。他曾经在所罗门公司组建了套利部，收罗了一批与别人格格不入的数学怪胎，这批最能赚钱的赌徒在华尔街赫赫有名。

而这一次，LTCM掌门人梅里韦瑟依旧选用了数学模型作为投资法宝。

斯科尔斯和默顿两位金融工程的著名学者，将金融市场的历史交易资料、已有的市场理论和市场信息有机结合在一起， 形成了一套较完整的电脑数学自动投资模型。

以“不同市场证券见不合理价差生灭自然性”为基础，LTCM利用计算机处理大量历史数据，通过精密计算得到两个不同金融工具间的历史价差作为参考。再综合市场信息分析最新价差，当发现不正常市场价差时，电脑立即建立起庞大的债券和衍性工具组合，进行套利。

套利建立在对冲操作上， 所谓对冲，就是在交易和投资中，同时进行两笔行情相关、方向相反、数量相当、盈亏相抵的交易，用一定的成本去“冲掉”风险，来获取风险较低或无风险利润 。LTCM主要从事所谓“趋同交易”，即寻找相对于其他证券价格错配的证券，做多低价的，沽空高价的，并通过加杠杆的方式将小利润变成大收益。

例如，在1996年，意大利、丹麦、希腊政府债券价格被低估，而德国债券价格被高估，根据数学模型预测，意丹希三国的债券与德国债券的的息差会随着欧元的启动而缩小， 于是LTCM大量买入低价 的意大利、丹麦、希腊的政府债券，卖空高价的德国债券。只要德国债券与意大利债券价格变化方向相同，当二者息差收窄时，就可以从中得到巨额收益。

后来，市场表现果然与LTMC的预测一致， 在高财务杠杆下，资金收益被无限放大。

这样的对冲组合交易，LTCM在同一时间持有20多种，每一笔核心交易都有着数以百计的金融衍生合约作为支持。 借助于复杂的数学估价模型，LTCM很快在市场上赚得盆满钵满。

成立短短4年，LTCM战绩赫赫，净资产增长速度极快。 到了1997年底，资本已达到了70多亿美元。 同时，每年的回报率平均超过40%，1994年收益率达到28%，1995年收益率高达59%，1996年收益率是57%。即使在东亚金融危机发生的1997年，也依然斩获25%的收益率。

这一系列记录以及合伙人的声望都使得投资人对LTCM情有独钟， 贝尔斯登、所罗门美邦、信孚银行、JP摩根、雷曼兄弟公司、大通曼哈顿银行、美林、摩根士丹利等 华尔街各大银行更是欲求成为投资者能分得一杯羹，裹挟着资本纷纷踏破门槛。

至此，LTCM如日中天。

LTCM造就的财富神话，一度使人惊叹不已，他们几乎从无亏损，没有波动，这简直就像是没有风险。著名的金融学家夏普疑惑不解地问斯科尔斯：“ 你们的风险在哪里？ ”

斯科尔斯也直挠头：没有人看到风险去哪里了。

在LTCM的操作中，斯科尔斯他们始终 遵循“市场中性”原则 ，即不从事任何单方面交易，仅以寻找套利空间为主，再通过对冲机制规避风险，使市场风险最小化。

在这一系列对冲组合的背后， 隐藏着无数控制风险的金融衍生合约，以及错综复杂的数学估价模型。 而最初开创了金融衍生时代、催生出一大批新生代“数量分析师”的布莱克-斯科尔斯方程，在LTCM战无不胜攻无不克的一路高歌中，可谓是立下了汗马功劳。

布莱克-斯科尔斯方程（Black-Scholes期权定价模型）简称B-S模型，最早于1973年由布莱克和斯科尔斯共同提出， 其思想来源于现代金融学中的一场“实践之旅”。

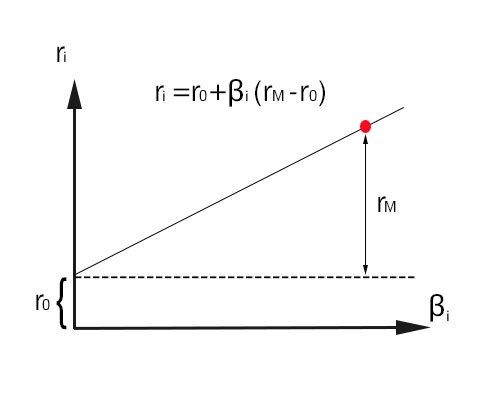
1952年，芝加哥大学一名博士生马科维茨用一篇论文点燃了现代金融学的大爆炸， 人类历史上第一次清晰地用数学概念定义和解释了“风险”和“收益”两个概念 ，把收益率视为一个数学的随机变量，证券的期望收益是该随机变量的数学期望，而风险则可以用该随机变量的方差来表示。60年代，马科维茨的学生夏普携手其他几人再续前缘，进一步推导出期望收益率与相对风险程度之间的关系，那就是金融学中最著名的资产定价模型（CAPM）。

布莱克的核心思想，就是在CAPM世界中寻找一个漂亮的衍生品定价数学模型。

从马科维茨开始，金融学就步入了一场理论与现实相结合的“实践之旅”，在那个思想熠熠生辉的年代，行为金融学日渐兴起。而70年代的“异端”布莱克，就在那个无套利分析法在舞台大放光彩的市场中，窥见了一套为金融衍生品投资行为量身定制的法宝。

无套利假定告诉我们， 在一定的价格随机过程假设下，每一时刻都可通过股票和股票期权的适当组合对冲风险，使得该组合变成无风险证券 ，这样就可以得到期权价格与股票价格之间的一个偏微分方程。只要解出这个偏微分方程，期权的价格也就随之而出。

布莱克和斯科尔斯两人借助于物理界一个热运动随机方程，再把f定义为依赖于股票价格的衍生证券的价格，一鼓作气推出了著名的B-S偏微分方程，这个方程就藏着衍生证券的价格。

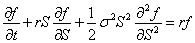
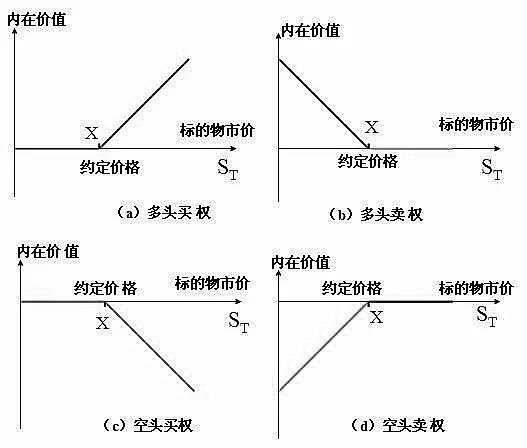
B-S偏微分方程令布莱克和斯科尔斯两人着迷不已，但也令他们抓耳挠腮。在苦苦思索后，布莱克选择 从欧式看涨期权入手 ，将未来期望收益值进行折现， 进一步解出看涨期权价格ct为：

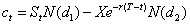
式中：

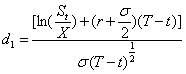
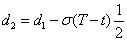
其中，N(x)是标准正态变量的累积分布概率,x服从N(0,1)。T为到期日,t为当前定价日,T-t是定价日距到期日的时间，St为定价日标的股票的价格,x为看涨期权合同的执行价格，r是按连续复利计算的无风险利率，σ是标的股票价格的波动率。

有趣的是，同年， 来自MIT的金融教授“期权之父”默顿也发现了同样的结论。

这三人相逢，便是一出高山流水的经典戏码，高手过招，惺惺相惜，碰撞出了更多期权思想的火花。谦逊的默顿一直等到布莱克模型公布后才发表自己的论文，甚至在后来还改进了模型，创造性地提出了 “看跌期权定价模型”，扩大了公式的应用范围。

欧式看涨期权和看跌期权之间存在着一种平价关系：

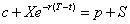
将这种平价关系同标准正态分布函数的特性结合起来：

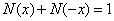
就可以得到欧式看跌期权的定价公式：

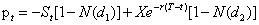
B-S模型刚推出之时，曾因完全脱离了经济学一般均衡的框架而被主流经济期刊视为“异端”不予接收， 不少经济学家大惊失色：怎么可以直接用无套利的方法给证券定价？ 但与模型定价惊人吻合的市场数据 ，让华尔街欣喜若狂、依旧不顾一切视其为掌中珍宝。

这一模型十分有效，是经济史以来应用最频繁的一个数学公式，它适用于其价格取决于标的证券价格S的所有衍生证券的定价，但要使其奏效， 还需满足一些复杂的假设：

1.证券价格st遵循几何布朗运动，即

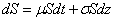
股价遵循几何布朗运动 ，意味着股价是连续的，它本身服从对数正态分布，资产预期收益率μ、证券价格波动的标准差σ为常数。在B-S定价公式中，受制于主观因素的μ并未出现，这似乎在告诉我们，不管你的主观风险收益偏好怎么样，都对衍生证券的价格不起波澜。

这其中，恰恰蕴含着风险中性定价的思想， 在风险中性的条件下，所有证券的预期收益率都等于无风险利率 。几何布朗运动的假设保证了股价为正（对数定义域大于0）、股价波动率、股票连续复利收益率服从钟形分布，这与实际股市数据也是较为一致的。

2.有效期内，无风险利率r为一个常数。无风险利率是一种理想的投资收益， 通常指国债一类没有风险的利率，到期不仅能收回本金，还能获得一笔稳定的利息收入。

3.标的证券没有现金收益支付，如有效期内的股票期权，标的股票不支付股利。

4.期权为欧式期权。欧式期权的买方不能在到期日前行使权利，而与之对应， 美式期权的买方可以在到期日前或任一交易日提出执行要求 ，“权利”更大，更复杂。

5.市场无摩擦，即不存在交易费用和税收，如印花税，以及所有证券交易都完全可分，投资者可以购买任意数量标的资产，如100股、10股、1股、0.1股等。

6. 证券交易 是连续的 。

7. 市场不存在无风险套利机会。即“天下没有白吃的午餐”，不存在不承受风险就获利这样的投资机会，想获得更高的收益就得承受更大的风险。

8.对卖空没有任何限制(如不设保证金)， 卖空所得资金可由投资者自由使用。

如果说，马科维茨的投资组合理论在金融学中画下了最基本的风险-收益框架，“第一次华尔街革命”爆发，现代投资证券业开始成为一个独立产业； 那布莱克-斯科尔斯方程则是“第二次华尔街革命”，金融衍生市场从此步入繁荣期，行为金融学为对冲基金的崛起提供有力的支持，金融学和金融实践的融合交错，现代金融大厦因此流光溢彩，一片星河灿烂。

站在时代浪潮之上，“数量分析专家”更是借助B-S模型创造出数十万亿金融衍生产品，全球经济财富指数级上升，美国金融行业一度升至社会所有行业的顶峰。可以说，这个公式，当之无愧为史上最“贵”的偏微分方程。

B-S模型与现实数据的惊人吻合， 使人们对这样一个简单有效的定价工具痴迷不已。

尤其随着巨额收益的日渐膨胀，许多银行家和交易员在欣喜若狂中也把这个方程当成了一种对冲风险的法宝，一种洞悉财富秘密的数学魔法。

而借助于B-S模型的强势助攻， 那只由梅里韦瑟组建的“梦幻组合”，也成为了金融舞台上最耀眼的明星。 这群惊才艳艳之人，是华尔街睥睨众生的骄傲存在，他们沉浸于几乎无往不利的B-S模型，沉溺于巨大杠杆财富的胜利中。

然盛极而衰，真正的风险正躲在数学模型里洋洋得意。

它们隐而不发，任凭一群天才嘲笑它们的无力弱小，准备着伺机而动，一举反攻。1997年亚洲金融危机爆发，风险呼啸着，砸向了那群骄傲得不可一世的人，将他们无情吞噬。

那压倒他们的最后一根稻草，来自于1998年8月17日俄罗斯的债务违约。

此后，巨星陨落，财神爷一夜之间从神坛跌入尘埃：

1998年上半年，LTCM亏损14%。

1998年9月初，资本金从年初的48亿美元掉落到23亿，缩水超过一半。

从5月俄罗斯金融风暴到9月全面溃败，短短的150天 资产净值下降90% ，LTCM出现43亿美元巨额亏损，仅余5亿美元，已走到破产边缘。噩耗一传来，一切都似乎无力回天，回头望去，LTCM曾经天使般的获利法宝，这一次却转变为了煞气腾腾的恶魔。

LTCM主要靠两大法宝获利：一为数学模型，二为杆杠对冲交易。

在斯科尔斯和默顿的手中，所有的市场数据都被收入到了运算中的电脑数学模型之中，被监控着的风险无处遁形，都可以被他们精确计算并控制。一旦市场存在着错误定价，他们就可以建立起庞大的债券及衍生产品的投资组合，进行套利投机活动。

然而他们忽略了，那个为金融衍生品交易定下基调的B-S模型，本身存在着的风险。

在LTCM的投资组合中，金融衍生产品占有很大的比重，但在Black—Scholes的期权定价公式中，暗含着这样的假设：

（1）交易是连续不断进行的。

（2）市场符合正态分布。

交易连续意味着市场不会出现较大的价格和行市跳跃、可以动态调整持仓来控制风险， 基于这个假设以及大数定律，我们很容易得到风险因子的变化符合正态分布或类正态分布 。

这是很多定价模型的基本假设，但事实并非如此。

市场并不是连续的，也根本不存在足够的交易来时刻保持风险动态平衡，很多无套利定价模型在这类假设下存在着瑕疵。 历史上出现过很多次跳变现象，市场跳变显示出市场并不符合正态分布，存在厚尾现象。 而在Black—Scholes期权定价公式中，d 作为一种非线性情况的线性风险估值，在价格剧烈变动的情况下同样失去了衡量风险的意义，当系统风险改变的时候，金融衍生工具的定价是具有很大不可估量性的，远非一个公式便可驾驭。

除此之外，在LTCM的数学模型中，它的假设前提和计算结果都是在历史统计数据基础上得出的， 但是历史数据的统计过程往往会忽略一些概率很小的事件。 这些事件一旦发生，将会改变整个系统的风险，造成致命打击，这在统计学上称为 “厚尾效应” 。

1998年俄罗斯的金融风暴就是这样的小概率事件， 而LTCM就是被这根稻草压死的。

在卫冕华尔街“最闪亮明星”征途中，LTCM想要借数学模型之手寻找常人难以发现的套利机会，为了达到这一目的， 他们选择了对冲交易，而为了放大收益，他们用了高杠杆。

LTCM利用从投资者筹得的22亿美元资本作抵押，买入价值1250亿美元证券，然后再以证券作为抵押，进行总值12500亿美元的其他金融交易，杠杆比率高达568倍。

高杠杆比率是LTCM追求高回报率的必然结果，但它却也是一把双刃刀。

对冲交易的作用建立在投资组合中两种证券的价格正相关的基础上， 但如果正相关的前提一旦发生改变，逆转为负相关，对冲就变成了一种高风险的交易策略，或两头亏损，或盈利甚丰 。在高杠杆比率下，对冲盈利可以暴增，亏损更可以陡加，负相关的小概率事件一发生，尾部风险带来的亏损足以让整个LTCM陷入万劫不复的境地，一招不慎就是满盘皆输。

这一次，LTCM高杠杆比率这一招就输了。

1998年8月17日，俄罗斯宣布债务违约，全球投资信心遭遇危机。

随之而来的就是全球市场开始暴跌，投资者不惜一切代价抛售手中债券。俄罗斯的破产让很多国际大银行遭受损失， 它们连夜召开紧急会议，要出售资产套现。

在这个惨淡的市场中，高杠杆比率要求LTCM拥有足够的现金支持保证金要求，LTCM曾经笃信市场哪怕因小概率事件偏离了轨道，但总会回归到正常水平的。可LTCM已经没有足够的现金了，它面临着被赶出赌场的危险， 流动性不足把它推向了危机的边缘 。

最后，利用历史数据预测证券价格相关性的数学模型也失灵了 。LTCM所沽空的德国债券价格上涨，它所做多的意大利债券等证券价格下跌， 对冲交易赖以生存的正相关变为负相关，小概率事件还是偷袭了市场 ，高杠杆下LTCM一切资产犹如打了水漂，通通血本无归。