深入浅出理解决策树算法(二)-ID3算法与C4.5算法
从
深入浅出理解决策树算法(一)-核心思想
文章中,我们已经知道了决策树最基本也是最核心的思想。
那就是其实决策树就是可以看
做一个if-then规则的集合。
我们从决策树的根结点到每一个都叶结点构建一条规则。
并且我们将要预测的实例都可以被一条路径或者一条规则所覆盖。
如下例:假设我们已经构建好了决策树,
现在买了一个西瓜,它的特点是纹理是清晰,根蒂是硬挺的瓜,你来给我判断一下是好瓜还是坏瓜,恰好,你构建了一颗决策树,告诉他,没问题,我马上告诉你是好瓜,还是坏瓜?
根据决策树的算法步骤,我们可以得到下面的图示过程:
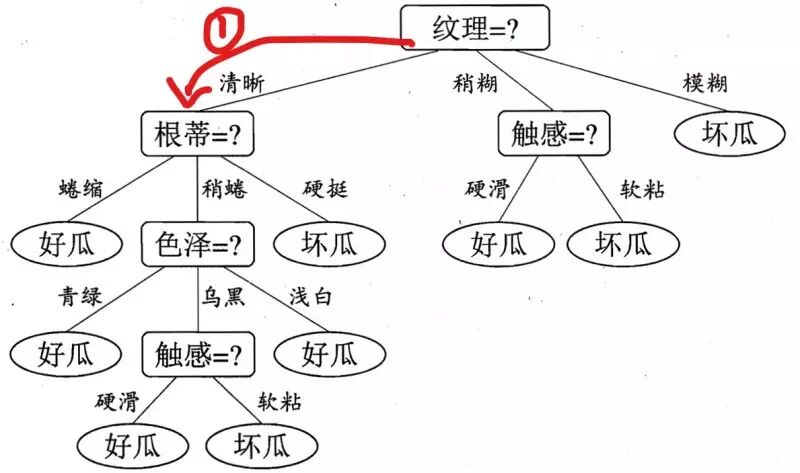
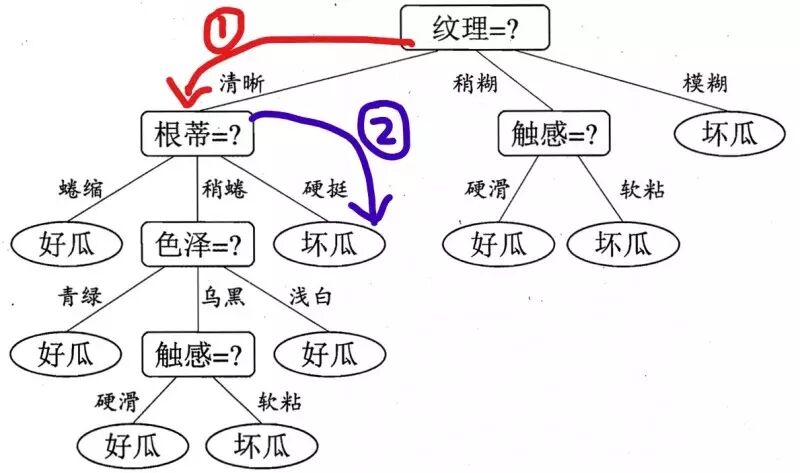
到达叶子结点后,从而得到结论。
我这个瓜的判断是坏瓜。(叶子结点就是类别了)
算法思路在上篇文章都讲解过,这里我们重点来说一下,在每一层的生长过程中,如何选择特征!
每一层选择好了特征之后,树也就自然建好了。
树建好了,也就万事大吉了(剪枝什么的暂时不讲),来了一个实例,我直接遍历树,到达叶子结点,就可以获取该实例的类别了。
决策树学习的关键其实就是选择最优划分属性,
希望划分后,分支结点的“纯度”越来越高。
那么“纯度”的度量方法不同,也就导致了学习算法的不同,这里我们讲解最常见的俩种算法,
ID3算法与C4.5算法。
我们既然希望划分之后结点的“纯度”越来越高,那么如何度量纯度呢?
“信息熵”是度量样本集合不确定度(纯度)的最常用的指标。
在我们的ID3算法中,我们采取信息增益这个量来作为纯度的度量。
我们选取使得信息增益最大的特征进行分裂!那么信息增益又是什么概念呢?
我们前面说了,
信息熵是代表随机变量的复杂度(不确定度)
通俗理解信息熵
,条件熵代表在某一个条件下,随机变量的复杂度(不确定度)
通俗理解条件熵
。
而我们这里说的的信息增益恰好是:信息熵-条件熵。
我们看如下定义:
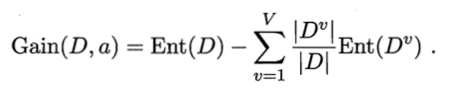
当前样本集合D 中第 k 类样本所占的比例为 pk(k其实是下标,微信不好打),则 D 的信息熵定义为
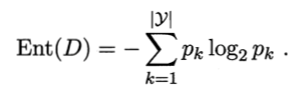
离散属性a 有 V 个可能的取值 {a1,a2,…,aV};样本集合中,属性 a 上取值为 av 的样本集合,记为 Dv。
用属性a 对样本集 D 进行划分所获得的“
信息增益”
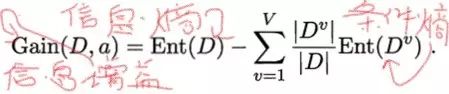
信息增益表示得知属性 a 的信息而使得样本集合不确定度减少的程度
那么我们现在也很好理解了
,在决策树算法中,我们的关键就是每次选择一个特征,特征有多个,那么到底按照什么标准来选择哪一个特征。
对于ID3算法来说,这个问题就可以用信息增益来度量。
如果选择一个特征后,
信息增益最大
(
信息不确定性减少的程度最大
),
那么我们就选取这个特征。
好的,我们现在已经知道了选择指标了,就是在所有的特征中,选择信息增益最大的特征。那么如何计算呢?看下面例子:
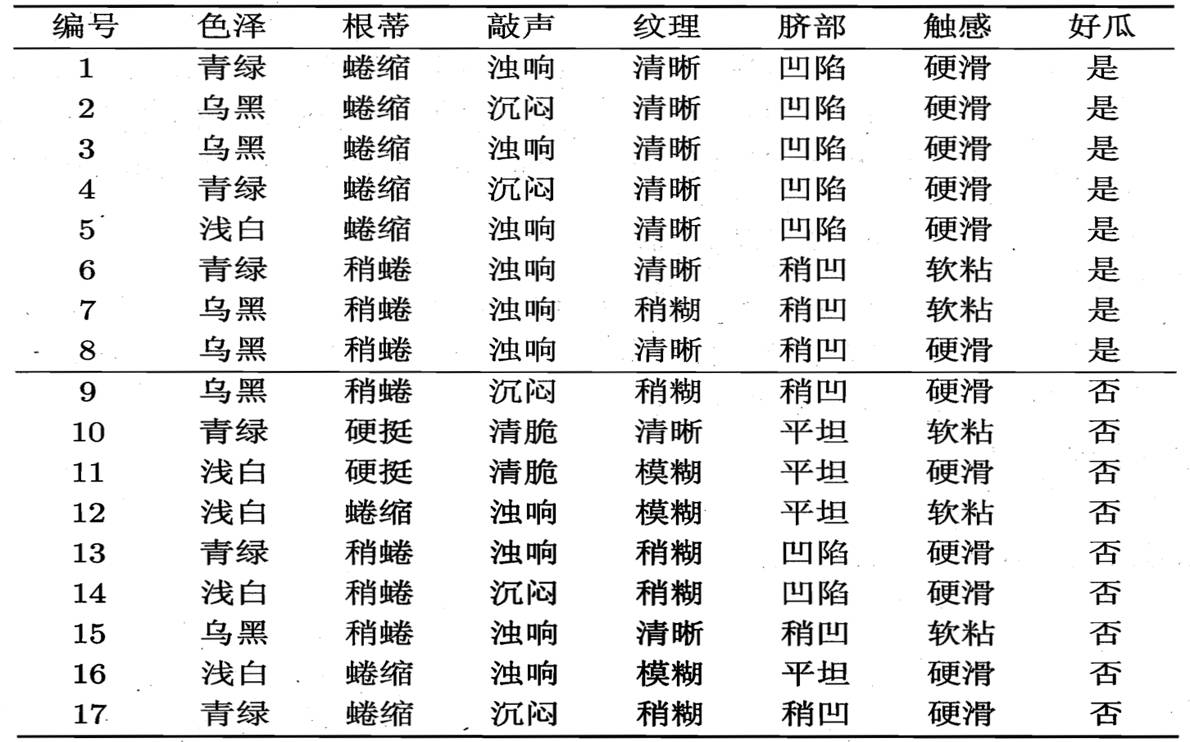
正例(好瓜)占 8/17,反例占 9/17 ,根结点的信息熵为
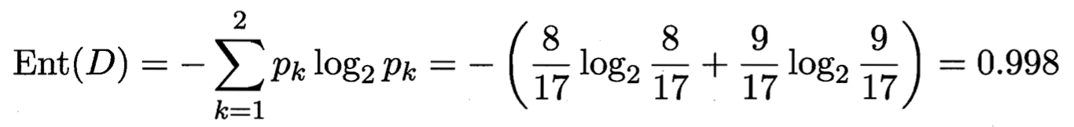
计算当前
属性集合
{色泽,根蒂,敲声,纹理,脐部,触感}中每个属性的信息增益
色泽有3个可能的取值:{青绿,乌黑,浅白}
D1(色泽=青绿) = {1, 4, 6, 10, 13, 17},正例 3/6,反例 3/6
D2(色泽=乌黑) = {2, 3, 7, 8, 9, 15},正例 4/6,反例 2/6
D3(色泽=浅白) = {5, 11, 12, 14, 16},正例 1/5,反例 4/5
3 个分支结点的信息熵
那么我们可以知道属性色泽的信息增益是:
同理,我们可以求出其它属性的信息增益,分别如下:
于是我们找到了信息增益最大的属性纹理,它的Gain(D,纹理) = 0.381最大。
所以我们选择的划分属性为“纹理”
如下:
根据纹理属性划分后,我们可以得到了三
个子结点。
对于这三个子节点,我们可以递归的使用刚刚找信息增益最大的方法进行选择特征属性,
比如:
D1(纹理=清晰) = {1, 2, 3, 4, 5, 6, 8, 10, 15},第一个分支结点可用属性集合{色泽、根蒂、敲声、脐部、触感},基于 D1各属性的信息增益,分别求的如下:
于是我们可以选择特征属性为根蒂,脐部,触感三个特征属性中任选一个(
因为他们三个相等并最大
)。
其它俩个子结点同理,然后得到新一层的结点,再递归的由信息增益进行构建树即可
我们最终的决策树如下:
啊,那到这里为止,我们已经知道了构建树的算法,上面也说了有了树,我们直接遍历决策树就能得到我们预测样例的类别。
那么是不是大功告成了呢?
结果是:不是的
我们从上面求解信息增益的公式中,其实可以看出,信息增益准则其实是对可取值数目较多的属性有所偏好!
现在假如我们把数据集中的“编号”也作为一个候选划分属性。我们可以算出“编号”的信息增益是0.998
因为每一个样本的编号都是不同的(
由于编号独特唯一,条件熵为0了,每一个结点中只有一类,纯度非常高啊
)。
也就是说,来了一个预测样本,你只要告诉我编号,其它特征就没有用了,
这样生成的决策树显然不具有泛化能力。
于是我们就引入了信息增益率来选择最优划分属性!
而信息增益率也是C4.5算法的核心思想。下面就讲解C4.5算法
这次我们每次进行选取特征属性的时候,不再使用ID3算法的信息增益,
而是使用了信息增益率这个概念。
首先我们来看信息增益率的公式:
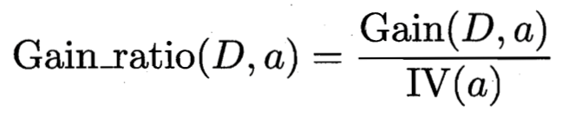
由上图我们可以看出,信息增益率=信息增益/IV(a),说明信息增益率是信息增益除了一个属性a的固有值得来的。
我们一开始分析到,
信息增益准则其实是对可取值数目较多的属性有所偏好!(
比如上面提到的编号,如果选取编号属性,每一个子节点只有一个实例,可取值数目是最多,而且子节点纯度最高《只有一个类别》,导致信息增益最大,所以我们会倾向于选他,但是已经分析了这种树是不具备泛化能力的
)。
但是刚刚我们分析到了,信息增益并不是一个很好的特征选择度量。于是我们引出了信息增益率。
我们来看IV(a)的公式:
属性a的固有值:
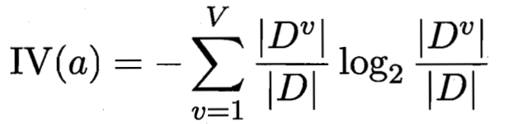
IV(触感) = 0.874 ( V = 2 )
IV(色泽) = 1.580 ( V = 3 )
IV(编号) = 4.088 ( V = 17 )
由上面的计算例子,可以看出IV(a)其实能够反映出,当选取该属性,分成的V类别数越大,IV(a)就越大,如果仅仅只用信息增益来选择属性的话,那么我们偏向于选择分成子节点类别大的那个特征。
但是在前面分析了,并不是很好,所以我们需要除以一个属性的固定值,
这个值要求随着分成的类别数越大而越小。于是让它做了分母。
这样可以避免信息增益的缺点。
因为一开始我仅仅用信息增益作为我的选择目标,但是会出现“编号”这些使得类别数目多的属性选择,但是又不具有泛化能力,所以我给他除以一个值(这个值)随着你分的类别越多,我就越大,一定程度上缓解了信息增益的缺点
那么信息增益率就是完美无瑕的吗?
当然不是,有了这个分母之后,我们可以看到增益率准则其实对可取类别数目较少的特征有所偏好!
毕竟分母越小,整体越大。
所以C4.5算法不直接选择增益率最大的候选划分属性,候选划分属性中找出信息增益高于平均水平的属性(
这样保证了大部分好的的特征
),再从中选择增益率最高的(
又保证了不会出现编号特征这种极端的情况
)
好的,ID3算法和C4.5算法的基本内容就讲完了,希望对大家有帮助~
参考:
周志华《机器学习》,例子来源于书籍
德川《全体机器学习会slides》,很多都是总结于ppt
致谢:
德川,宇轩师兄





