电路大师课系列-模拟集成电路设计第五讲:基本π网络（下）

编者按：UCLA以电路方向的研究和教学闻名于世界，Behzad Razavi教授和Asad Abidi教授更是世界闻名的电路大师。UCLA的研究生课程模拟集成电路设计（EE215A）正是由Razavi和Abidi两位大师轮流授课。我们整理了其中精华部分与大家分享:)

前情回顾：

电路大师课系列-模拟集成电路设计第一讲:绪论与线性时不变系统

电路大师课系列-模拟集成电路设计第二讲:传输函数，零极点的形成及时域响应

电路大师课系列-模拟集成电路设计第三讲:零极点与频率响应

电路大师课系列-模拟集成电路设计第四讲:基本π网络（上）

同学们， 助教哥 虽然回国吃香喝辣，但是并没有乐不思蜀，这次携手 UCLA 研究生 焦魔 给大家带来基本 π 网络（下）。

三电容电路

作为基本 π 网络的一种，三电容电路是理解模拟电路频响、放大器稳定性、开关 - 电容放大器、开关 - 电容积分器、采样保持放大器的基础。从多种不同的角度深刻理解三电容电路是模拟电路设计入门的关键，同时 三电容电路也是各大电路公司面试常用的题型 。

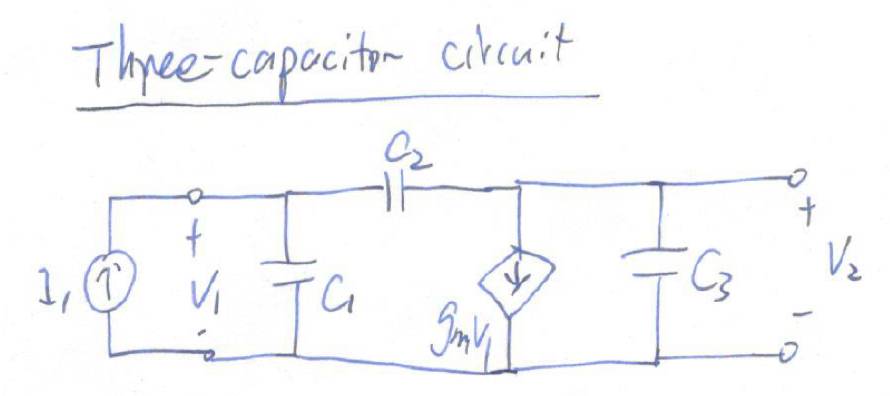
首先，这个电路有三个电容，但是三个电容形成一个环，电路只有两个独立的状态变量（ state variable ），所以这个电路的传输函数只有两个极点。

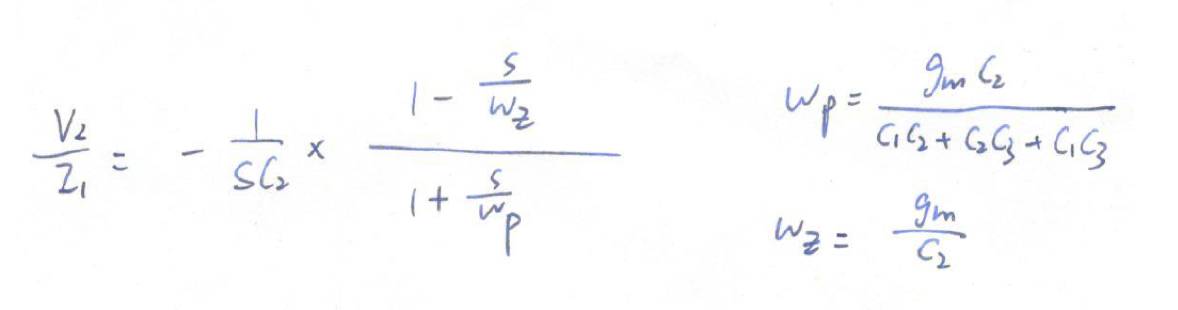
现在我们根据上一期讲的 基本 π 型函数列出传输函数 V ₂ /I ₁ （不记得的同学可以去 电路大师课系列-模拟集成电路设计第四讲:基本π网络（上） 回顾一下）：

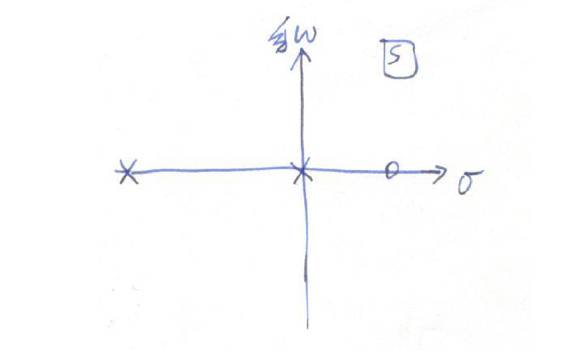
零极点的位置如下图，有一个极点在原点，注意有一个零点在右半平面。

假设拉普拉斯域 I ₁ (s) 为 1 ，或者时域 i ₁ (t) 为 1*δ(t) ，我们可以通过拉普拉斯反变换找出 v ₂ (t) ：

我们发现， v ₂ (t) 由一个阶跃项和一个指数项组成，指数项会衰减到 0 ，但是阶跃项会一直保持。合在一起的总响应就是 一开始有一个反向的过冲（ overshoot ），然后会以指数衰减的方式稳定到一个固定的终值。

现在我们换一种方式来分析零极点。之前我们讲过，极点是由电路的纯粹的拓扑结构所定的，每一个网络函数都有一样的极点。

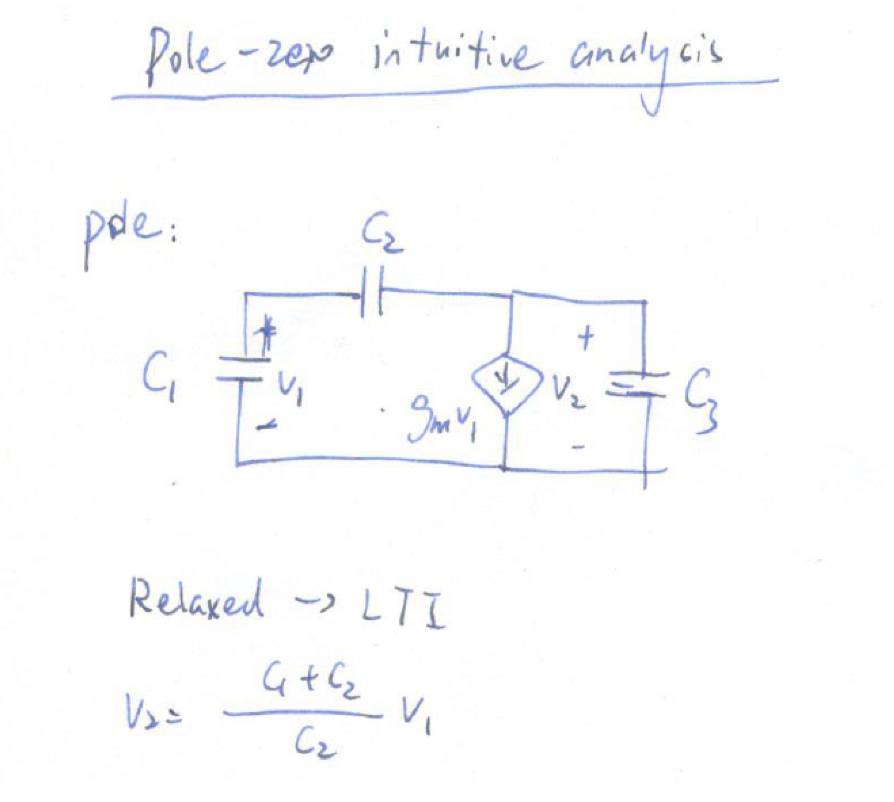
三电容电路零极点分析

现在我们来看这个纯粹的电路。假设这个电路是零状态的（ relaxed ），那么这个电路是线性时不变的（ LTI ），所以 C ₁ C ₂ 组成了一个分压器，那么我们可以用 V ₁ 来表示 V ₂ 。

但是 V ₂ 由是受控源两端的电压，而这个受控源也受到 V ₁ 的控制，所以就变成了压控电流源被自己两端电压所控制。 一个被自己电压控制的电流源就是一个电阻 。所以我们可以算出该电阻：

于是，三电容电路变成了下图。这个电路的时间常量很好算了，算出来果然跟我们之前算的一个极点吻合。

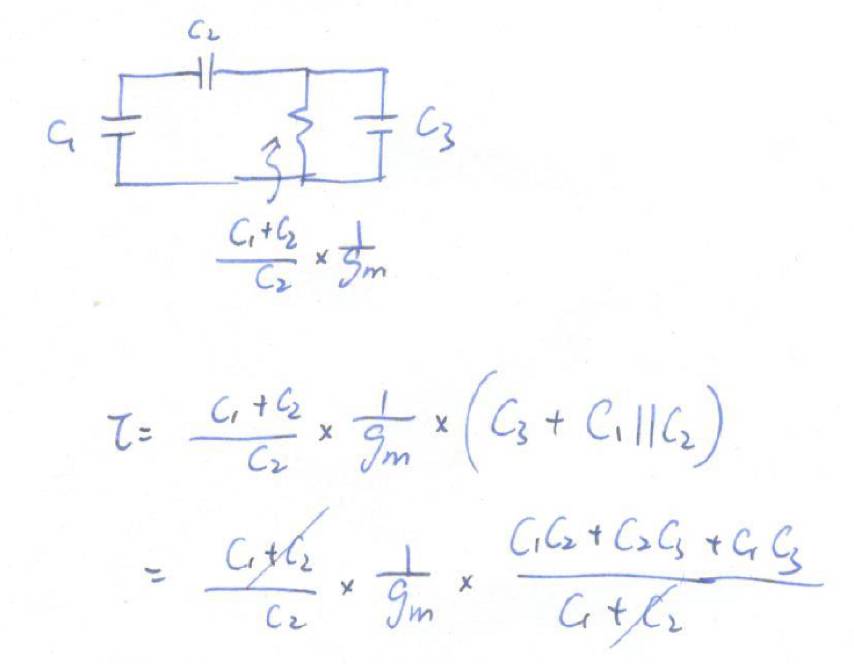
另一个极点呢？

我们现在假设 C ₂ C ₃ 上的 t=0- 时的初始状态为这样：

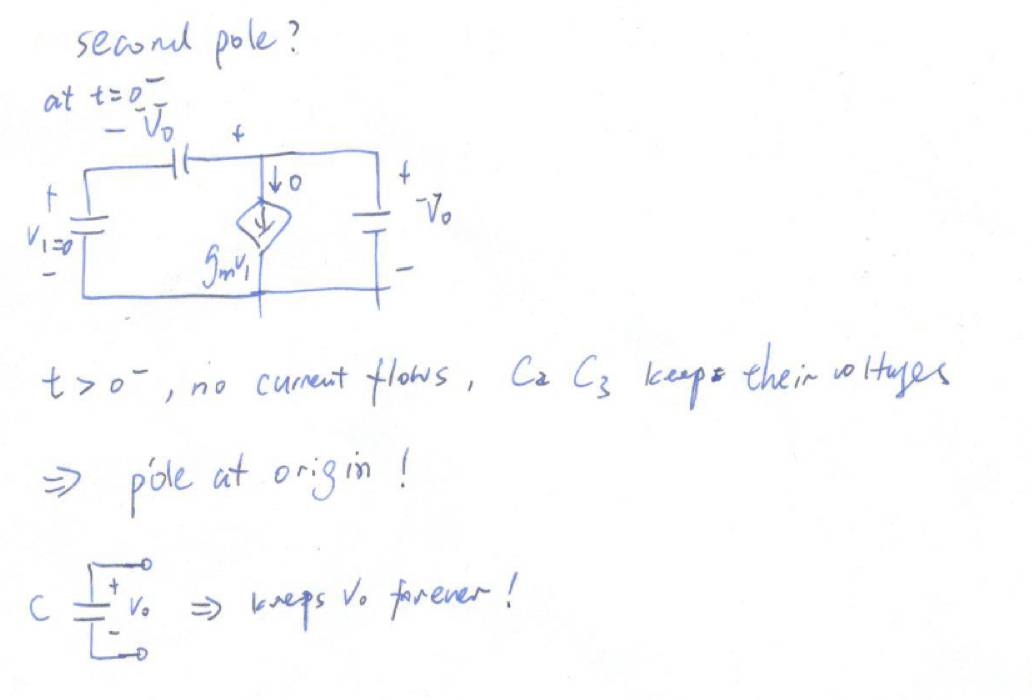
当 t=0 时，我们发现整个电路没有电流， C ₂ C ₃ 上的电压一直保持着，这种能够保持初始状态的网络，一定有一个极点在原点。我们可以举一个最简单的例子，一个电容可以保持电压，所以电容的阻抗这个网络函数有一个极点在原点。

这也与我们之前的推导吻合。

现在找零点，我们之前学过，零点是很特别的，是由激励和响应的相对位置决定的。找零点需要抵消响应。现在我们把响应 V ₂ 抵消掉，如图：

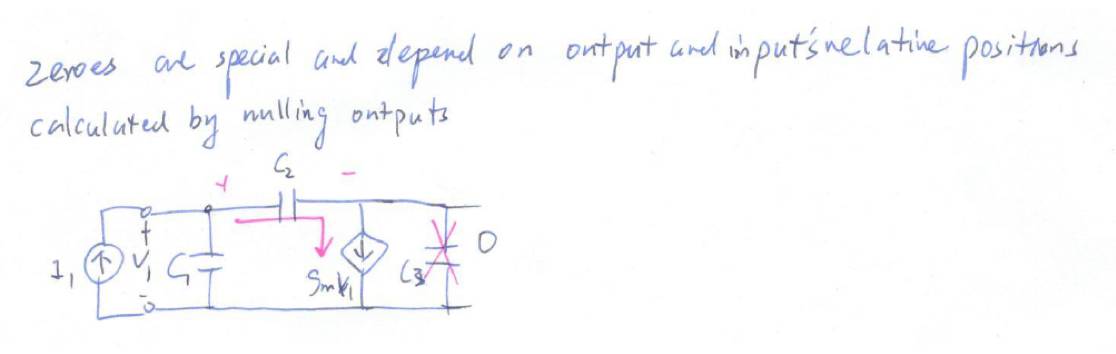
那么 C ₃ 没有电流，受控源的电流等于 C ₂ 的电流，但是 C ₂ 的电流由可以被直接用 V ₁ 表示出来，所以：

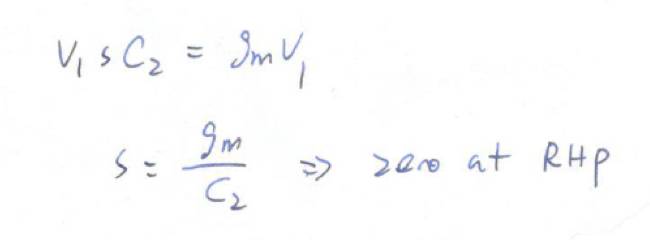
三电容电路时域分析

然后， 我们从时域的角度把三电容电路的机理再过一次 （非常重要！是深入理解三电容电路并帮你通过面试拿到offer的关键！）。

我们必须要先理解冲激电流的物理意义。单位冲激电流在拉普拉斯域的表示为 1 。注意这个 1 是有单位的，单位是库伦，大家可以思考一下为什么电流的拉普拉斯转换的单位是库伦。 在时域里，单位冲激函数前面的 1 的单位也是库伦，因为单位冲激函数的积分为 1 ，但是电流的积分必须是库伦，所以这里的 1 代表了一个包裹的 1 库伦电荷，这个 1 库伦的电荷只需要 0 时间就可以被输送，因为在 t=0 的时候，电流无穷大。

所以，单位冲激电流的物理意义就是用 0 时间通过无穷大的电流向一个高斯面里输送了 1 库伦电荷。

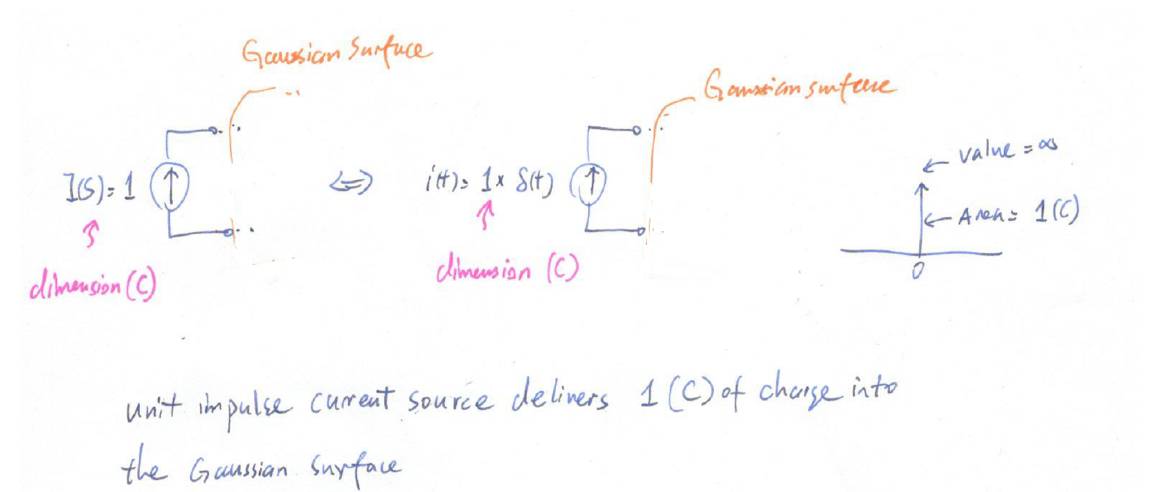
现在回到三电容电路，在 t=0- 时，三个电容都没有初始电荷。在 t=0 时， 1 库伦的电荷被注入到了红色高斯面里。现在的问题是，会不会有有限量的电荷在 t=0 时流入绿色高斯面。我们来分析这个情况：

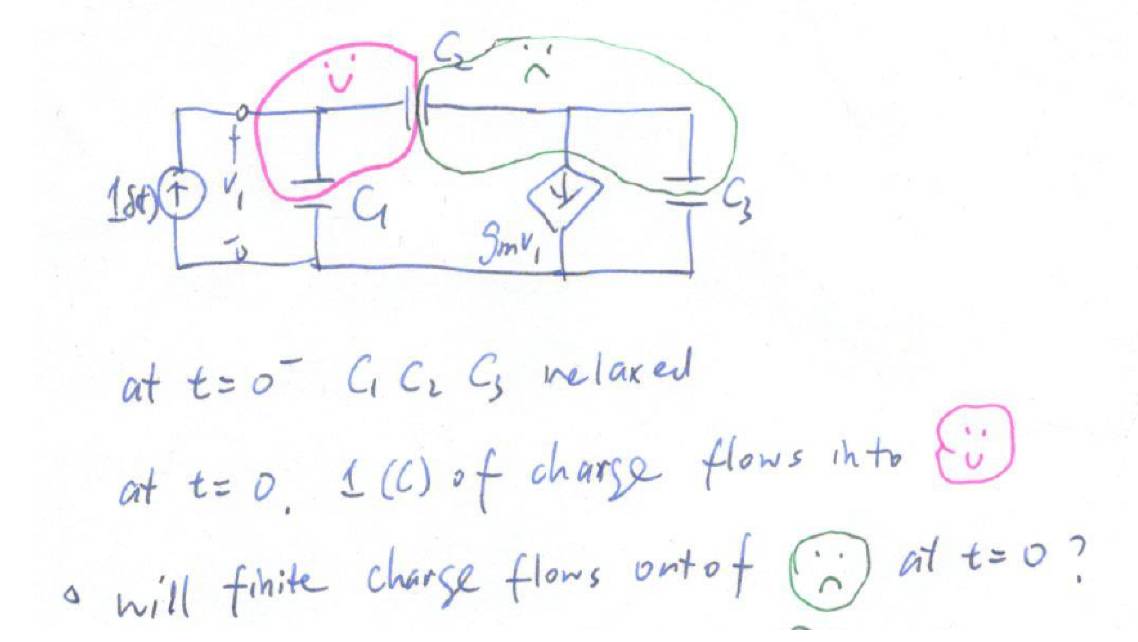
如果有有限量的电荷流入绿色高斯面，那说明受控源 g _m v ₁ 必须是无穷大，因为无穷大的电流才能在 0 时间内输送有限的电荷，有限的电流在 0 时间内输送 0 电荷。

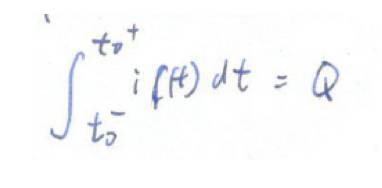
这表示 v ₁ 是无穷大，但是 v ₁ 无穷大的话，红色高斯面内必须有无穷大的电荷，这不可能，因为冲激电流所携带的电荷是有限的。所以受控源电流是有限的，受控源在 0 时间内不输送任何电荷。所以在 t=0+ 时，只有电荷会在 C ₁ C ₂ C ₃ 中重新分布， 1 库伦的电荷会在 C ₁ +C ₂ ||C ₃ 这个总电容上建立一个电压 v ₁ (0+) 。 C ₂ 和 C ₃ 必须形成一个分压器，因为 C ₂ 的右极板和 C ₃ 的上极板的电荷总和为 0 。这样我们可以推出 v ₂ (0+) ：

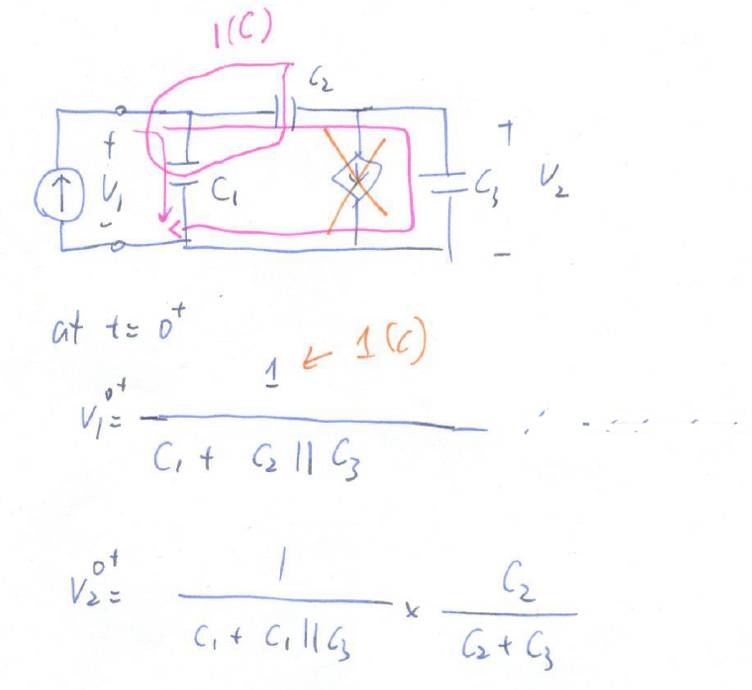
化简 v ₂ (o+) ，我们可以得到：

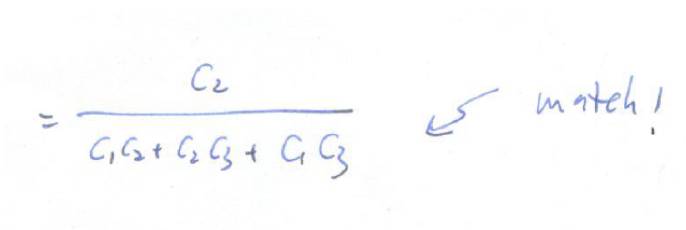
这跟我们之前用拉普拉斯转换得到的结果一致 ！

下面看最终状态，当电路达到最终状态时，所有的状态变量都不再改变了（除非我们有共振或者不稳定的特殊情况，然而这个电路显然没有），这说明受控源 g _m v ₁ 必须为 0 ， v ₁ 必须为 0 。但是当 t>0 时，红色高斯面内的电荷就不再会改变了，因为独立电流源为 0 ，所以所有 1 库伦的电荷都必须被 “ 挤压 ” 到 C ₂ 上，产生电压 1/C ₂ 。因为 v ₁ (∞) 为 0 ，所以我们可以算出 v ₂ (∞) 为 -1/C2 。

这又跟我们用拉普拉斯转换得到的结果一致 ！

我们之已经分析过，这个电路只有一个非无穷大的时间常量，所以这是一个 “ 准一阶电路 ” 。对于这种电路，只要我们知道在 t=0+ 的初始值和 t=∞ 的终值，中间的行为就是一个一阶指数衰减。所以我们得到与之前一致的响应：

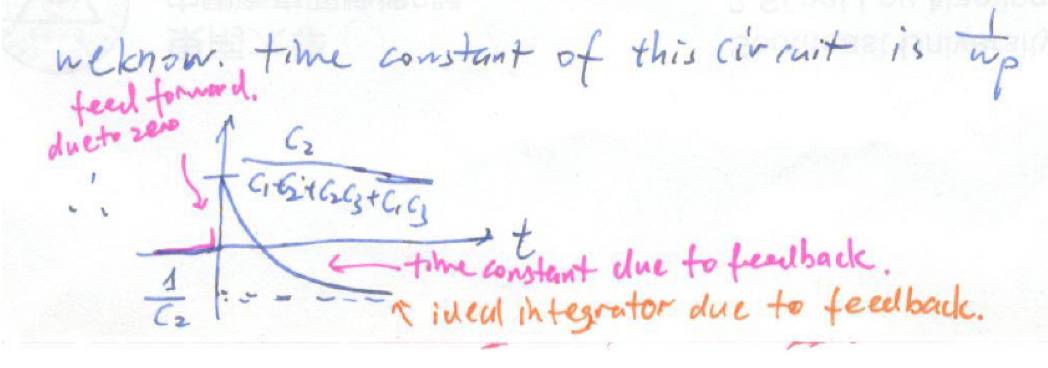
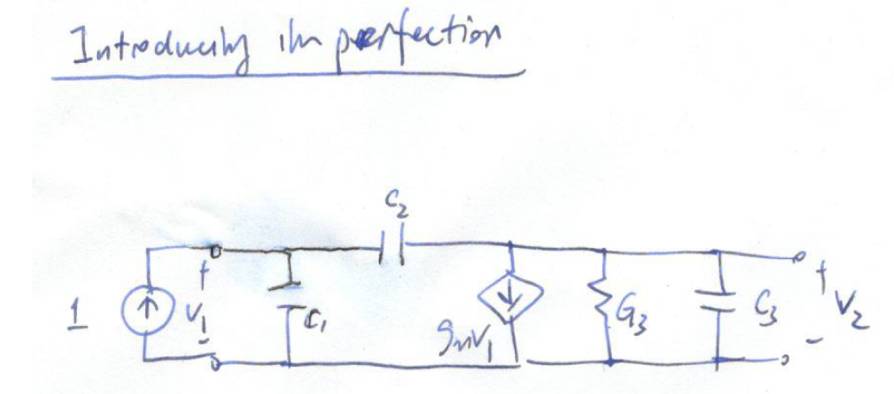
引入非理想效应

接着我们引入一个不理想效应，在受控源处并联一个电导 G ₃ （有没有觉得下面的电路图很熟悉？对了，就是MOSFET小信号电路基本就长这样）。

重新使用 基本 π 型函数列出传输函数：

使用拉普拉斯反变换，我们得到

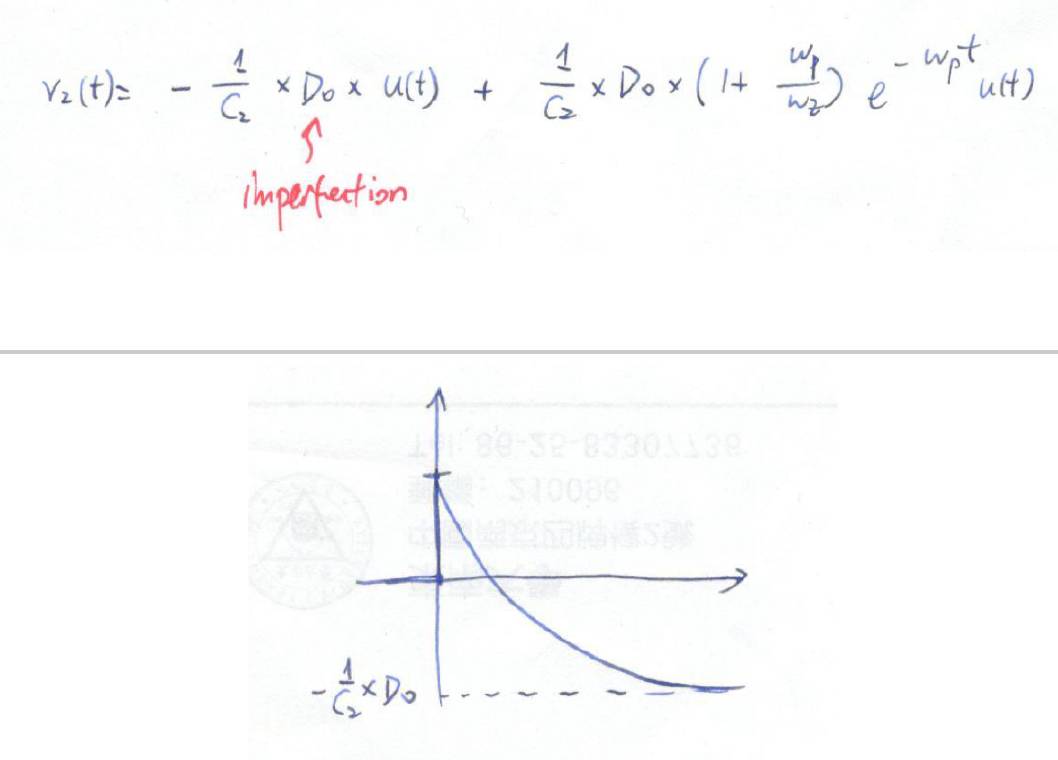
这里， D ₀ 成为了误差项，如果要让 D ₀ 非常接近于 1 ， g _m R ₃ 要远大于 1+C ₁ /C ₂ 。

我们来从时域角度看这个问题：

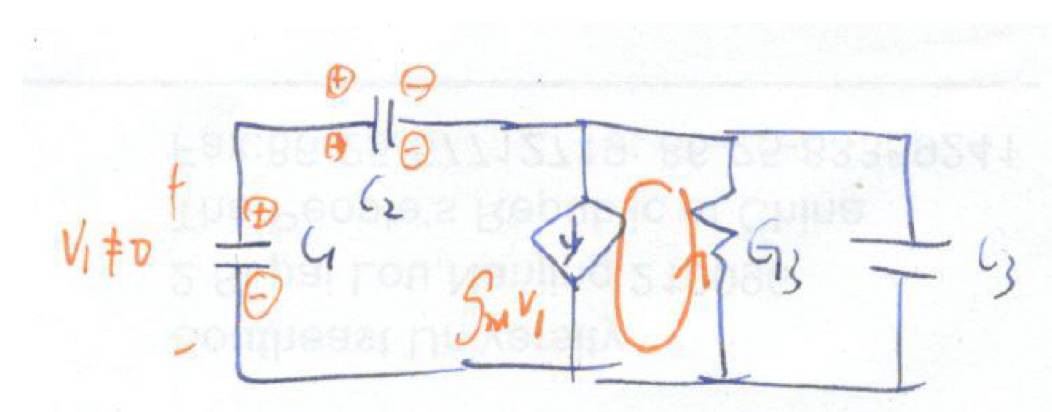
如果 G ₃ 不为 0 ，那么在终值状态时，会有一个循环的电流流过 G ₃ 。所以 g _m v ₁ 不为 0 ，那么 v ₁ 不为 0 。这样，并非所有的 1 库伦电荷都被 “ 挤压 ” 到了 C ₂ 上，这就是导致误差项的原因。对于模拟电路而言，我们希望精确地放大信号，放大倍数最好是元件之间的比例。假如我们的冲激电流源变成了 v _s C ₁ δ(t) ，或者说 C ₁ 采样了一个电压源 v _s ， C ₁ 在 t=0 时被放置到三电容电路里，如果 G ₃ 为 0 ，那么响应 v ₂ 终值将为准确的电容比例 -C ₂ /C ₁ v _s 。但如果 G ₃ 不为 0 ，这个比例就会有误差。

三电容电路实际应用

看到这里，大家一定会认为我们会拿MOSFET小信号电路作为例子吧？非也，我们当然要找一个更有趣的例子。下面由 焦魔 为大家讲一个三电容电路的实例：开关电容积分器（ SCIntegrator ）。

开关电容积分器是有源梯形滤波器（ Active Ladder Filter ）的基本组成模块。相比于使用电阻电容有源滤波器（ OpAmp RC Filter ），开关电容滤波器（ SC Filter ）具有精度高，噪声小，受工艺、电压、温度影响小的优点（原因是我们不再需要电阻这个在芯片上很难做准的元件了）。下图所示为一种基本的开关电容积分器（前向欧拉型， Forward Euler ）的电路。

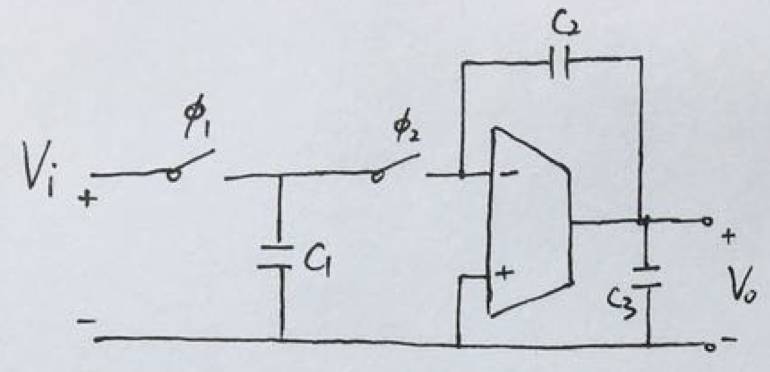
注：在该电路图中，梯形符号代表跨导放大器（ Operational Transconductance Amplifier,  OTA ）。跨导放大器和我们熟悉的运算放大器非常容易混淆，前者使用梯形符号，后者则是三角形符号。运算放大器的模型是一个压控电压源，跨导放大器的模型是一个压控电流源。严格来讲，我们通常所说的集成电路中的运算放大器实际上都是指跨导放大器；而我们做板级电路设计时使用的运放芯片才是真正的运算放大器。

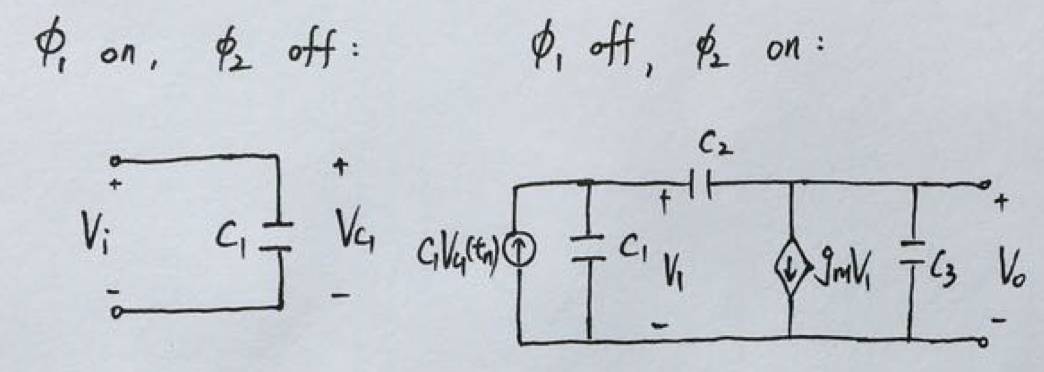
该电路有两个工作相位。在 φ ₁ 相位，电容 C ₁ 的电压跟随输入电压 v _i 变化， φ ₁ 相位结束时电容 C ₁ 的电压即为 φ ₂ 相位开始时的初始电压。 φ ₂ 相位时电路的小信号模型如下图右侧所示。其中冲激电流源等效代表了 C ₁ 的初始电压。电路的时序和波形图如下：

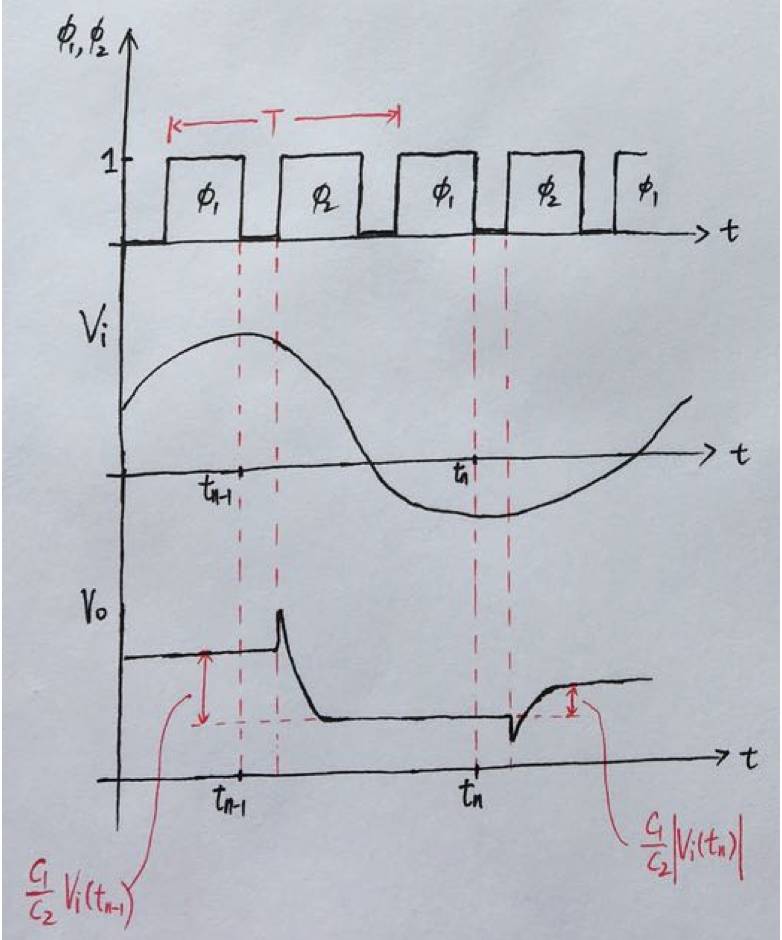
电容 C ₁ 在每个周期的采样值在 t k 时刻确定，输出电压在每个周期 φ ₂ 的开始时刻开始变化，先有一个瞬时的前向馈通，然后以指数衰减的形式稳定到最终的电压值，理想情况下电压的变化量由电容 C ₁ 和 C ₂ 的比值以及 t k 时刻采样的输入电压值决定。同时，上一个周期存在 C ₂ 上的电荷并没有被释放，所以这个电路就变成了一个积分器。如果考虑 OTA 有限的输出电阻，这个电压变化量会有一定的偏差。

小编们写得可辛苦了，特别是手绘图，经常要重画好几遍。大家如果觉得有帮助的话，就多多给小编输送核桃吧！