啊~昨晚躺了一个小时竟然没有睡着,美容觉泡汤了...于是竟然大半夜起来写了这篇文章
在《逻辑回归到神经网络》中,小夕让神经网络冒了个泡。在《一般化机器学习与神经网络》中,将神经网络这一火热的模型强制按回机器学习一般框架里。在《BP算法的本质》里,详细的阐述了BP算法的本质与目标。
好啦~这一篇回到简单、纯粹的状态,我们来一起戳一戳可爱的神经细胞。
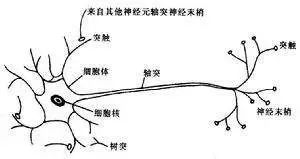
学生物的人眼里的神经细胞:
学数学与机器学习的人眼里的神经细胞:
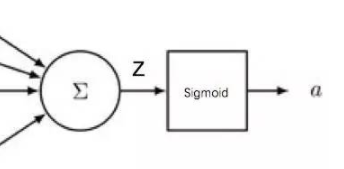
看,其实神经元就是一个小小的生命,它会用树突接收外面世界的多维信息,然后在它小小的脑袋里计算一下,来对当前外面的世界作出一个反应,这个反应通过轴突传递出去。
看,是不是也很像一个小小的机器学习模型呢?一个将多维的输入X转换成输出信号y的小模型。

那么,假如我们发现了好几堆(层)可爱的神经元,并且惊讶的发现它们可以交互信息,一起完成任务,但是我们并不知道它们之间怎么连接的。那怎么办呢?
我们当然可以给它们两两之间分配一条线呀。这个线就代表两个神经元之间的连接强度,如果两个神经元之间没有连接,这根线的值就是0,连接的越紧密,值就越大。
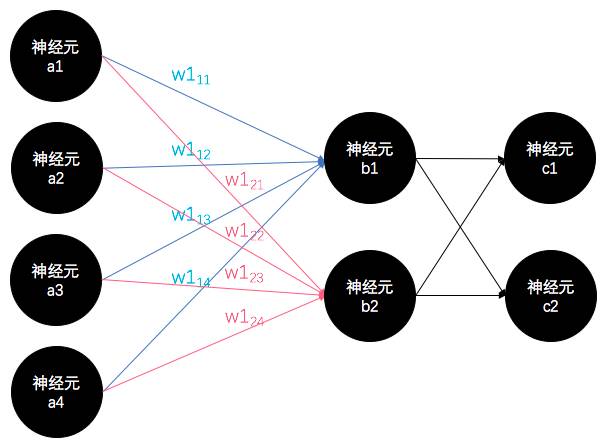
看。
这么多可爱的神经元一起工作的时候,在数学家眼里,其实并不复杂:
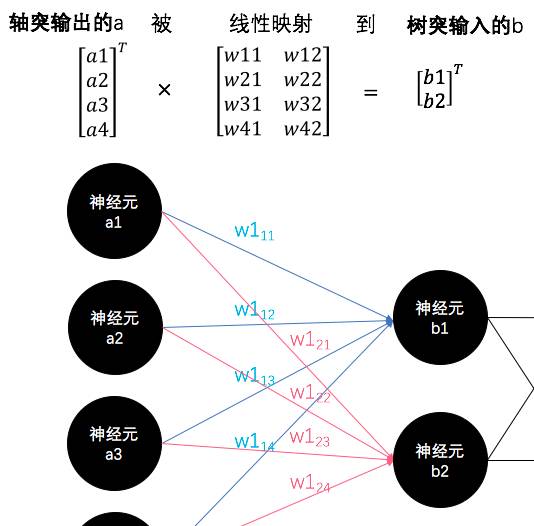
前一层的神经元的轴突(输出信号)与下一层的神经元的树突(输入)的信号传递过程,其实就是一个线性映射的过程。
补充:
想一想,《线性代数一》中,小夕是不是已经讲啦,对待矩阵,一个非常重要的视角就是“映射”。矩阵,可以表示一个映射函数,准确的说是一个线性映射函数。
看,就像上图中虽然每个人都知道,b=a*W(矩阵乘法),但是有没有人想过“线性映射”这一层含义呢?其实呀,下一层的树突b收到的信号,就是上一层的轴突a经过W(这个大众眼里的矩阵)线性映射而成的。
前一层神经元们的信号经过线性映射,传递到下一层的神经元树突那里后,当然下一步就是经过神经元的细胞体啦。

而生物学上的神经元细胞体是干什么的呢?当然就是将树突的信号转换成轴突的信号啦。所以,它是一个生物信号的转换器!
而我们知道,多个线性映射叠加之后依然是线性映射。所以哪怕你叠加再多的线性映射,整体的函数依然是个线性函数,这也太鸡肋啦。所以细胞体决不能同流合污,它要完成复杂而神秘的信号转换,也就是数学上的非线性映射!
而非线性映射的灵活度就一下子无限大了,有无数的非线性函数可以完成这个非线性映射的过程:
比如,Sigmoid函数:
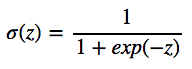
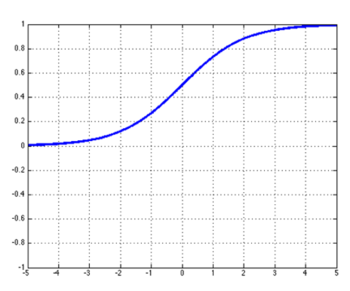
tanh函数:
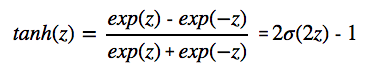
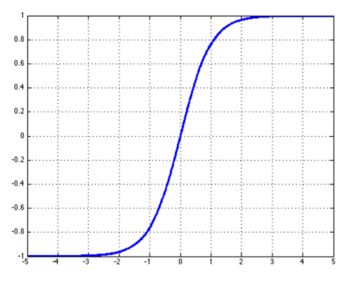
Hard tanh函数:
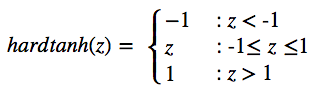
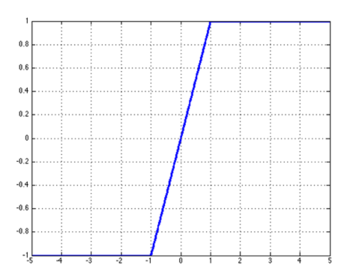
Soft sign函数:
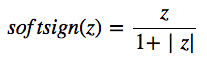
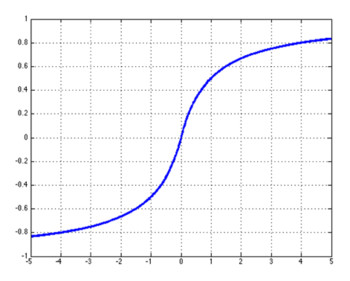
ReLU函数:
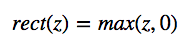
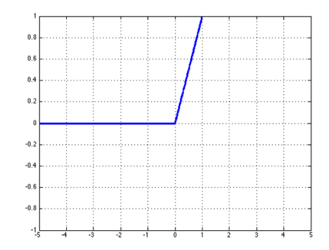
Leaky ReLU函数:
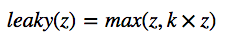
其中0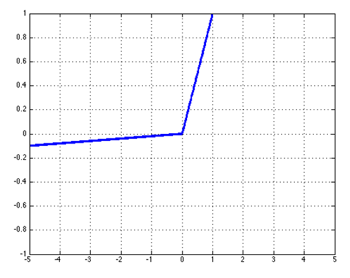
没错,这些单调上升的非线性函数都可以当做神经网络的激活函数,在不同的任务中,总有一个在该任务中表现最好的激活函数。
所以,将视角拉的更远一些:
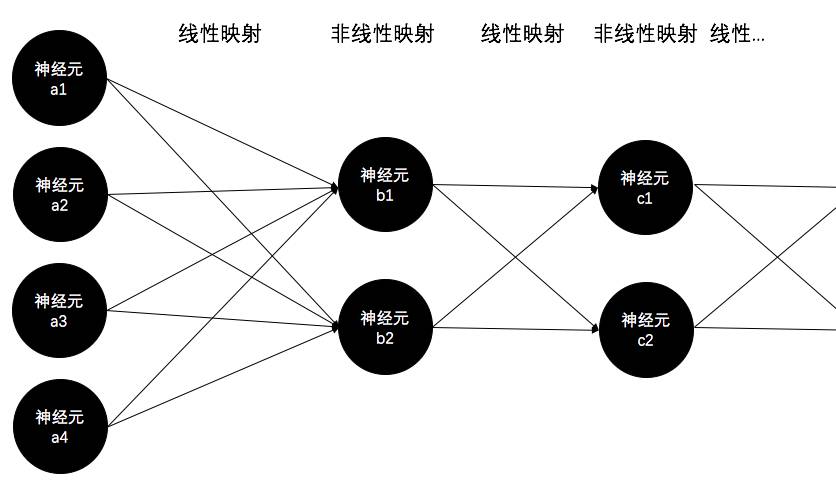
那么有没有一个通用的最优激活函数呢?
只能等生物学家把神经元的细胞体研究透彻着再说啦。
所以,激活函数的选择,准确的说是构造,目前就是一个黑匣子。所以很难解释清楚为什么ReLU函数在图像相关的任务中往往表现的比广为人知的Sigmoid、tanh更好,恐怕只有你体内的神经元自己知道啦~快想办法让它告诉你呀~

同样的道理,为什么非要选择单调上升的函数呢?就不能用y=sin(x)这种非单调的吗?就不能用单调下降的吗?
答:首先是激活函数的生物学依据,激活函数模仿的也是神经细胞的实验特性——当树突的输入足够强时,就会让细胞体兴奋,从而在轴突输出一个兴奋信号。而当细胞体对树突的输入不感兴趣或者它认为不够强时,就处于抑制态,在轴突输出的信号很弱,或者说相当于输出电路中的低电平。除此之外,就是依靠大量面向任务的选择经验+少量感性推理+少量理性推理。也就是说,这个问题并没有被严谨的否决,所以不要轻易说不可以哦。

而具体的什么函数在什么领域,什么任务中表现的好,大家就自己去积累经验吧。也有很多博客和论文有讲这些经验性的trick。比如在斯坦福大学的CS224D课程(自然语言处理与深度学习)中,就有较为详细的讲解。
下面这个是CS224D的中文笔记(不是我记的),这篇文章里的激活函数的公式和仿真图也是从这里直接抠出来的。作者笔记里还有这些激活函数的导函数等,建议没时间刷视频的可以看这个笔记:
http://blog.csdn.net/han_xiaoyang/article/details/51711134
还有一篇文章也比较有营养:
http://www.cnblogs.com/pinard/p/6437495.html
还有一篇论文,数学差的就要慎重些了:
Mhaskar H N, Micchelli C A. How to choose an activationfunction[J]. Advances in Neural Information Processing Systems, 1994: 319-319.









