干货 | 相机标定：机器人手眼标定

相机标定是机器人视觉中非常重要的一步，可以帮助机器人转换识别到的视觉信息，从而完成后续的控制工作，例如视觉抓取等等。笔者做过一些机器人手眼标定的工作，在此用尽量简单的语言来描述下机器人手眼标定的流程。本文的目的在于让大家对于相机标定有一个感性的认知，能够知道不同条件下机器人手眼标定的流程，具体的实现方法及技术细节还需要大家自行google。

▌ 1. 坐标系标定通用方法

机器人手眼标定其实就是两个坐标系之间转换关系的标定。假设现在有两个坐标系robot和camera，并且我们已知对应的几个固定点 在这两个坐标系的坐标 和 。那么根据坐标系转换公式，我们可以得到：

[1]

上式中 就代表我们希望求出来的相机到机器人的转换矩阵。 和 为补1后的“齐次坐标”： ，这样我们的齐次坐标变换矩阵 便可以同时包含旋转以及平移。

只要学过线性代数的同学应该都清楚，式[1]相当于就是一个N元一次方程，只要点 的个数大于我们求解的转换矩阵维度同时这些点线性不相关，我们便可以通过伪逆矩阵计算出来 ：

[2]

计算出来的坐标变换矩阵便可以直接应用于后续的坐标变换。现在计算出来的矩阵允许坐标进行旋转，平移，以及任意方向的缩放。如果想要把这个坐标矩阵变成刚性的变换矩阵，只需要将其左上角的旋转矩阵正交化即可，但是加了这个约束后有可能降低坐标变换精度，即刚性变换矩阵约束太多，造成欠拟合。

当坐标变换存在非线性变换时，我们也可以设计并训练一个神经网络 直接拟合两组坐标之间的关系：

[3]

当然一般情况下，式[2]中的线性矩阵便足以描述机器人和相机之间的坐标转换关系。引入神经网络进行非线性拟合，训练集的拟合精度会非常高，但是当训练点个数不足的时候，会发生过拟合，使得实际测试时拟合精度反而降低。

通过以上的计算我们可以知道，只要我们能够同时测量出来固定点 在两个坐标系的坐标 和 并且测量出来多组数据，我们就可以很方便地计算出来坐标变换矩阵。当然在实际过程中我们有可能很难同时测量出来固定点 在两个坐标系的坐标，在后面我会分相机和机器人的情况讨论如何用一些小trick来尽量实现这个测量目标，如何进行标定，以及如何进行标定精度的验证。

▌ 2. 相机放置在固定位置，与机器人分开（eye-to-hand）

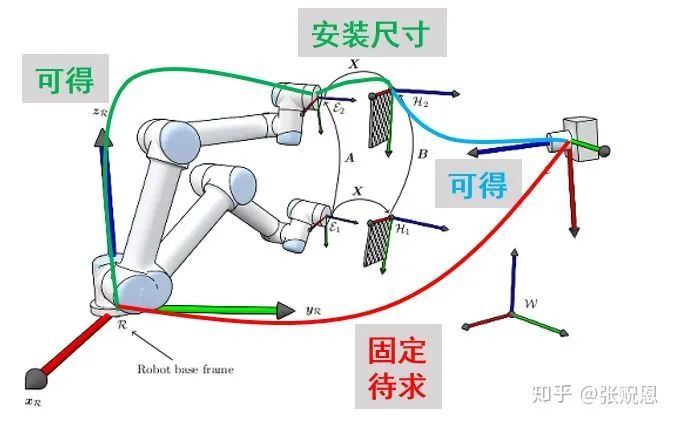
Fig 1. 机器人eye-to-hand标定

我们应该养成一个习惯，即遇到问题时先考虑我们的待求量和已知量。如Fig 1 所示。在eye-to-hand的问题中，待求量为相机到机器人基座坐标系的固定转换矩阵 。注意我们这里用的base而不是robot来表示机器人基座坐标系，因为需要与机器人其他部分的坐标系进行区分。机器人基座坐标系是固定不动的，而其他的关节，例如机器人末端坐标系end，是不断变化的。考虑到相机是固定在一个位置，因此相机只有相对于基座坐标系才是固定不动的，这样我们的待求量 是一个固定参数，标定才有意义。

根据我们在节1中讨论的，我们接下来需要测量几组固定点 在机器人基座坐标系下的坐标 和 在相机坐标系下的坐标 。那么怎么去测量这些点的坐标呢？接下来我们需要用到一个标定神器：棋盘格。

Fig 2. 棋盘格及角点识别

如Fig 2所示，我们可以通过相应的视觉算法准确地识别棋盘格的角点，具体算法在opencv，python，matlab，和ros等常用平台中都有包装好的函数，直接调用即可，在此不进行赘述。

通过识别棋盘格，我们便可以得到棋盘格角点在相机坐标系的坐标 ，但是这是二维坐标，通过相机内参和物体的深度信息我们可以计算出来 ，这个我们之后会分为3D相机和2D相机进行讨论。我们可以假设已经测量出来了 ，接下来我们只要测量出来对应的棋盘格点在机器人中的坐标 ，便可以标定出来机器人和相机之间的转换矩阵 。棋盘格在标定的时候，会固定在机器人的末端，而机器人的末端坐标系（end）到基座坐标系（base）可以通过机器人正向运动学计算得到。那么我们可以通过如下关系测量出来棋盘格点在机器人基座坐标系的坐标 ：

[4]

式[4] 中， 和 分别代表机器人末端坐标系（end）到基座坐标系（base）的转换矩阵和棋盘格坐标系（board）到机器人末端坐标系（end）的转换矩阵。其中 可以实时根据机器人正运动学得到，而 可以通过设计一个固定尺寸的棋盘格得到。当棋盘格尺寸以及安装固定后，我们可以设棋盘格的左上角点为原点，然后测量或者根据设计尺寸得到棋盘格原点到机器人末端坐标原点的平移坐标。另外棋盘格平面一般与机器人末端平面平行，这样该原点的法向量也知道了，接下来便可以计算得到 。 代表棋盘格角点在棋盘格坐标系下的坐标，这个同样根据设计棋盘格的尺寸得到。另外我们需要注意棋盘格的角点在机器人坐标系和在图像坐标系的顺序需要一一对应，但是一般的方形棋盘格会有旋转对称的问题，即我们无法区分出来棋盘格的原点是左上角点还是右下角点，因此手眼标定时我们也可以用下面的非对称棋盘格。

Fig 3. 非对称棋盘格及角点识别，旋转180度可以区分左上角点跟右下角点

当我们根据式[4]计算得到棋盘格角点在机器人基座坐标系中的坐标 ，然后根据图像识别加相机内参和深度信息得到棋盘格在相机坐标系中的坐标 ，我们便可以根据节1所述的方法计算得到相机到机器人的转换矩阵：

[5]

接下来我会再讨论如何将棋盘格在图像中的坐标 ，转换为棋盘格在相机坐标系中的坐标 。

2.1  3D相机

相机的图像坐标为二维坐标，代表了在图像中的行和列数。将二维的图像坐标转换为在相机坐标系的三维坐标，是基于需要用到相机的内参公式和深度值:

[6]

式[6]中 为目标点的深度值，3D相机能够测出来目标点的深度，从而能够计算出目标点的3维坐标。列数 和行数 为目标点在图像中的坐标。 代表目标点在相机坐标系下的三维坐标。 和 为焦距，用于描述像素单位和三维坐标单位之间的比例关系。 和 为相机光心在图像中的投影位置，用于计算图像原点和相机坐标系原点之间的位移。

我们通过求逆矩阵，可以根据目标点的图像坐标计算得到其三维坐标 。相机内参一般相机提供方会给出，有的相机提供方还会直接提供计算好的三维点云信息。如果相机提供方只给出了一个深度图，也没有给相机内参，则需要我们通过张正友标定法，标定出来相机的内参。opencv，python，matlab等提供了完善的内参标定工具包，可以直接使用。

Fig 4. 相机内参解释

2.2 2D相机

2.2.1 基于平面深度z进行目标3D坐标估计

在节2.1中我们说明了3D相机的情况下由2D图像坐标转换到3D相机坐标系的方法。如果我们使用的是2D相机，那么我们便缺失了深度信息，也就是式[6]中的 ，因此2D相机一般用于一个平面的物体识别。这样我们只需要估计出一个平面的 坐标，然后便可以根据式[6] 计算得到目标点在相机坐标系下的三维坐标 。

2.2.2 基于平面参考点集进行目标3D坐标估计

另外当2D相机只用于识别平面上物体的位移和旋转时，我们也可以直接通过下面这个方法直接估计目标点的位置和旋转。

Fig 5. 非垂直坐标系下目标点的表示

如Fig 5所示，我们可以通过摆放三个标志物于相机视野的角落，这样识别出来三个位置点 在图像坐标系中的坐标 , , 。然后我们可以构建平行四边形，用两个坐标轴的向量去计算目标点在图像坐标系的坐标 。注意这里的坐标轴不需要是直角坐标轴，从而更加符合实际情况，因为实际贴标志物时不可能做到两条坐标轴完全垂直。

[7]

[8]

[9]

接下来，我们在机器人末端安装探针，通过触碰标志物，得到这三个位置点在机器人基座坐标系的坐标 , , ，这三个点应该在一个平面上。因为式[9]计算出来的是一个比例关系，因此根据相似三角形的原理，我们可以计算出目标点点在机器人基座坐标系base的坐标 :

[10]

通过式[7]-[10]我们可以发现，通过建立一个平面中三个参考点的非直角坐标系，然后就可以将目标点的图像坐标 转换为在机器人基座坐标系的三维坐标