
栈(stack)又称之为堆栈是一个特殊的有序表,其插入和删除操作都在栈顶进行操作,并且按照先进后出,后进先出的规则进行运作。
如下图所示
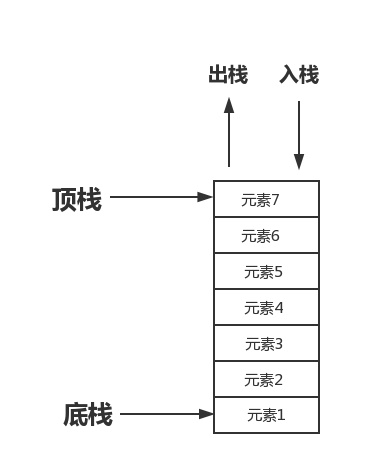
例如枪的弹匣,第一颗放进弹匣的子弹反而在发射出去的时候是最后一个,而最后放入弹匣的一颗子弹在打出去的时候是第一颗发射出去的。
栈的接口
如果你创建了一个栈,那么那么应该具有以下接口来进行对栈的操作
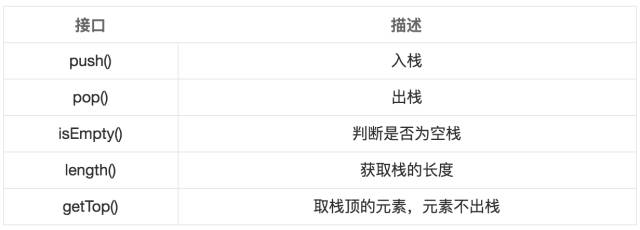
知道栈需要上述的接口后,那么在Python中,列表就类似是一个栈,提供接口如下:
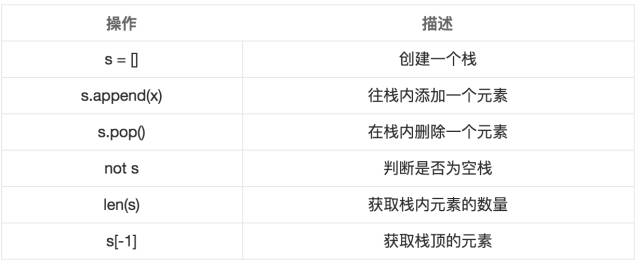
Python中的栈接口使用实例:
# 创建一个栈
In
[
1
]
:
s
=
[]
# 往栈内添加一个元素
In
[
2
]
:
s
.
append
(
1
)
In
[
3
]
:
s
Out
[
3
]
:
[
1
]
# 删除栈内的一个元素
In
[
4
]
:
s
.
pop
()
Out
[
4
]
:
1
In
[
5
]
:
s
Out
[
5
]
:
[]
# 判断栈是否为空
In
[
6
]
:
not
s
Out
[
6
]
:
True
In
[
7
]
:
s
.
append
(
1
)
In
[
8
]
:
not
s
Out
[
8
]
:
False
# 获取栈内元素的数量
In
[
9
]
:
len
(
s
)
Out
[
9
]
:
1
In
[
10
]
:
s
.
append
(
2
)
In
[
11
]
:
s
.
append
(
3
)
# 取栈顶的元素
In
[
12
]
:
s
[
-
1
]
Out
[
12
]
:
3
一大波实例
在了解栈的基本概念之后,让我们再来看几个实例,以便于理解栈。
括号匹配
题目
假如表达式中允许包含三中括号()、[]、{},其嵌套顺序是任意的,例如:
正确的格式
{()[()]},[{({})}]
错误的格式
[(]),[()),(()}
编写一个函数,判断一个表达式字符串,括号匹配是否正确
思路
-
创建一个空栈,用来存储尚未找到的左括号;
-
便利字符串,遇到左括号则压栈,遇到右括号则出栈一个左括号进行匹配;
-
在第二步骤过程中,如果空栈情况下遇到右括号,说明缺少左括号,不匹配;
-
在第二步骤遍历结束时,栈不为空,说明缺少右括号,不匹配;
解决代码
建议在pycharm中打断点,以便于更好的理解
#!/use/bin/env python
# _*_ coding:utf-8 _*_
LEFT
=
{
'('
,
'['
,
'{'
}
# 左括号
RIGHT
=
{
')'
,
']'
,
'}'
}
# 右括号
def
match
(
expr
)
:
"""
:param expr: 传过来的字符串
:return: 返回是否是正确的
"""
stack
=
[]
# 创建一个栈
for
brackets
in
expr
:
# 迭代传过来的所有字符串
if
brackets
in
LEFT
:
# 如果当前字符在左括号内
stack
.
append
(
brackets
)
# 把当前左括号入栈
elif
brackets
in
RIGHT
:
# 如果是右括号
if
not
stack
or
not
1
<=
ord
(
brackets
)
-
ord
(
stack
[
-
1
])
<=
2
:
# 如果当前栈为空,()]
# 如果右括号减去左括号的值不是小于等于2大于等于1
return
False
# 返回False
stack
.
pop
()
# 删除左括号
return
not
stack
# 如果栈内没有值则返回True,否则返回False
result
=
match
(
'[(){()}]'
)
print
(
result
)
迷宫问题
题目
用一个二维数组表示一个简单的迷宫,用0表示通路,用1表示阻断,老鼠在每个点上可以移动相邻的东南西北四个点,设计一个算法,模拟老鼠走迷宫,找到从入口到出口的一条路径。
如图所示
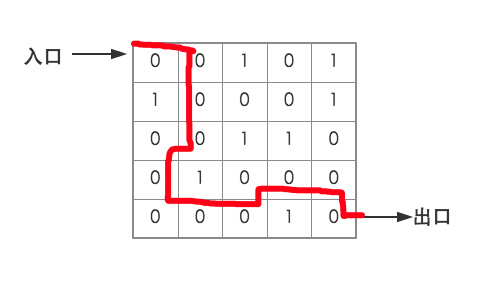
出去的正确线路如图中的红线所示
思路
-
用一个栈来记录老鼠从入口到出口的路径
-
走到某点后,将该点左边压栈,并把该点值置为1,表示走过了;
-
从临近的四个点中可到达的点中任意选取一个,走到该点;
-
如果在到达某点后临近的4个点都不走,说明已经走入死胡同,此时退栈,退回一步尝试其他点;
-
反复执行第二、三、四步骤直到找到出口;
解决代码
#!/use/bin/env python
# _*_ coding:utf-8 _*_
def
initMaze
()
:
"""
:return: 初始化迷宫
"""
maze
=
[[
0
]
*
7
for
_
in
range
(
5
+
2
)]
# 用列表解析创建一个7*7的二维数组,为了确保迷宫四周都是墙
walls
=
[
# 记录了墙的位置
(
1
,
3
),
(
2
,
1
),
(
2
,
5
),
(
3
,
3
),
(
3
,
4
),
(
4
,
2
),
# (4, 3), # 如果把(4, 3)点也设置为墙,那么整个迷宫是走不出去的,所以会返回一个空列表
(
5
,
4
)
]
for
i
in
range
(
7
)
:
# 把迷宫的四周设置成墙
maze
[
i
][
0
]
=
maze
[
i
][
-
1
]
=
1
maze
[
0
][
i
]
=
maze
[
-
1
][
i
]
=
1
for
i
,
j
in
walls
:
# 把所有墙的点设置为1
maze
[
i
][
j
]
=
1
return
maze
"""
[1, 1, 1, 1, 1, 1, 1]
[1, 0, 0, 1, 0, 0, 1]
[1, 1, 0, 0, 0, 1, 1]
[1, 0, 0, 1, 1, 0, 1]
[1, 0, 1, 0, 0, 0, 1]
[1, 0, 0, 0, 1, 0, 1]
[1, 1, 1, 1, 1, 1, 1]
"""
def
path
(
maze
,
start
,
end
)
:
"""
:param maze: 迷宫
:param start: 起始点
:param end: 结束点
:return: 行走的每个点
"""
i
,
j
=
start
# 分解起始点的坐标
ei
,
ej
=
end
# 分解结束点的左边
stack
=
[(
i
,
j
)]
# 创建一个栈,并让老鼠站到起始点的位置
maze
[
i
][
j
]
=
1
# 走过的路置为1
while
stack
:
# 栈不为空的时候继续走,否则退出
i
,
j
=
stack
[
-
1
]
# 获取当前老鼠所站的位置点
if
(
i
,
j
)
==
(
ei
,
ej
)
:
break
# 如果老鼠找到了出口
for
di
,
dj
in
[(
0
,
-
1
),
(
0
,
1
),
(
-
1
,
0
),
(
1
,
0
)]
:
# 左右上下
if
maze
[
i
+
di
][
j
+
dj
]
==
0
:
# 如果当前点可走
maze
[
i
+
di
][
j
+
dj
]
=
1
# 把当前点置为1
stack
.
append
((
i
+
di
,
j
+
dj
))
# 把当前的位置添加到栈里面
break
else
:
# 如果所有的点都不可走
stack
.
pop
()
# 退回上一步
return
stack
# 如果迷宫不能走则返回空栈
Maze
=
initMaze
()
# 初始化迷宫
result
=
path
(
maze
=
Maze
,
start
=
(
1
,
1
),
end
=
(
5
,
5
))
# 老鼠开始走迷宫
print
(
result
)
# [(1, 1), (1, 2), (2, 2), (3, 2), (3, 1), (4, 1), (5, 1), (5, 2), (5, 3), (4, 3), (4, 4), (4, 5), (5, 5)]
后缀表达式求值
题目
计算一个表达式时,编译器通常使用后缀表达式,这种表达式不需要括号:

编写程序实现后缀表达式求值函数。
思路
-
建立一个栈来存储待计算的操作数;
-
遍历字符串,遇到操作数则压入栈中,遇到操作符号则出栈操作数(n次),进行相应的计算,计算结果是新的操作数压回栈中,等待计算
-
按上述过程,遍历完整个表达式,栈中只剩下最终结果;
解决代码
#!/use/bin/env python
# _*_ coding:utf-8 _*_
operators
=
{
# 运算符操作表
'+'
:
lambda
op1
,
op2
:
op1
+
op2
,
'-'
:
lambda
op1
,
op2
:
op1
-
op2
,
'*'
:
lambda
op1
,
op2
:
op1
*
op2
,
'/'
:
lambda
op1
,
op2
:
op1
/
op2
,
}
def
evalPostfix
(
e
)
:
"""
:param e: 后缀表达式
:return: 正常情况下栈内的第一个元素就是计算好之后的值
"""
tokens
=
e
.
split
()
# 把传过来的后缀表达式切分成列表
stack
=
[]
for
token
in
tokens
:
# 迭代列表中的元素
if
token
.
isdigit
()
:
# 如果当前元素是数字
stack
.
append
(
int
(
token
))





