近些年来大有颠覆之势的深度学习起源于何方?或许在亚里士多德时代这一思想就已经存在了吧。近日,来自卡内基梅隆大学的计算机科学学院语言技术研究所的 Haohan Wang 和 Bhiksha Raj 与计算机科学学院机器学习系的邢波(Eric P. Xing)这三位研究者在 arXiv 上发布了一篇论文《On the Origin of Deep Learning》,详细地梳理了深度学习思想自亚里士多德时代以来的发展,尤其是现代随着计算机科学的兴起而出现的一些新的算法思想。鉴于该论文的篇幅较长,机器之心在此对其摘要和引言进行了编译介绍,对后面的详细内容则仅梳理了目录。有兴趣阅读原文的读者可在 https://arxiv.org/abs/1702.07800 查阅。
论文标题:深度学习起源(On the Origin of Deep Learning)

摘要
本论文是一篇深度学习模型演化历史的概述。本文涵盖的范围从研究大脑的联结主义(associationism)模型时的神经网络的出现到主宰深度学习领域近十年研究的模型(比如卷积神经网络(CNN)、深度信念网络(DBN)和循环神经网络(RNN)),并且还扩展到了最近流行的模型,比如变自编码器(VAE)和生成对抗网络(GAN)。除了对这些模型进行概述之外,这篇论文主要关注了上述模型的先前思想,探究了这些初始思想是如何组合构建成早期模型以及这些早期模型又是如何发展成它们当前的形式的。这些演化路径中有许多都持续了半个世纪以上的时间,而且演化方向各有不同。比如,CNN 构建于之前对生物视觉系统的知识上;DBN 则由图模型的建模能力与计算复杂度之间的权衡演化而来;而今天的很多模型都是古老的线性模型的神经形式。本论文对这些演化路径进行了概述,并提供了一个对这些模型的发展方式的简明的思考流程,旨在提供一个对深度学习的透彻背景。更重要的是,本论文还沿着这条路径总结了这些里程碑的要点,并提出了许多可以引导未来深度学习研究的方向。
引言
在目标检测、语音识别、机器翻译等许多不同的人工智能任务中,深度学习已经极大地提升了这些任务上的最佳表现水平(LeCun et al., 2015)。其深度架构的本质赋予了深度学习解决许多更加复杂的人工智能任务的可能性(Bengio, 2009)。由此,研究者在将深度学习应用到目标检测、面部识别或语言模型等传统任务的同时,也在将其扩展到许多不同的现代领域和任务中,比如 Osako et al. (2015) 使用循环神经网络来给语音信号降噪,Gupta et al. (2015) 使用堆栈自编码器(stacked autoencoders)来发现基因表达的聚类模式,Gatys et al. (2015) 使用一种神经模型来生成不同风格的图像,Wang et al. (2016) 使用深度学习来实现同时对多个模式的情感分析等等。这段时间是见证深度学习研究蓬勃发展的时代。
但是,为了从根本上推动深度学习研究的前沿进展,研究者需要透彻地理解历史上出现过哪些尝试以及当前的模型具有当前的形式的原因。这篇论文总结了多种不同的深度学习模型的演化历史,并解释了这些模型背后的主要思想以及它们与之前的思想的关系。要理解过去的工作并不容易,因为深度学习已经演化了很长一段时间,如表 1 所示。因此,这篇论文的目标是为读者提供一个深度学习研究领域重大里程碑的概览。我们将会覆盖表 1 中的里程碑,同时还会提及许多其它工作。为了表达清晰,我们将这个演化故事分成了不同的章节。
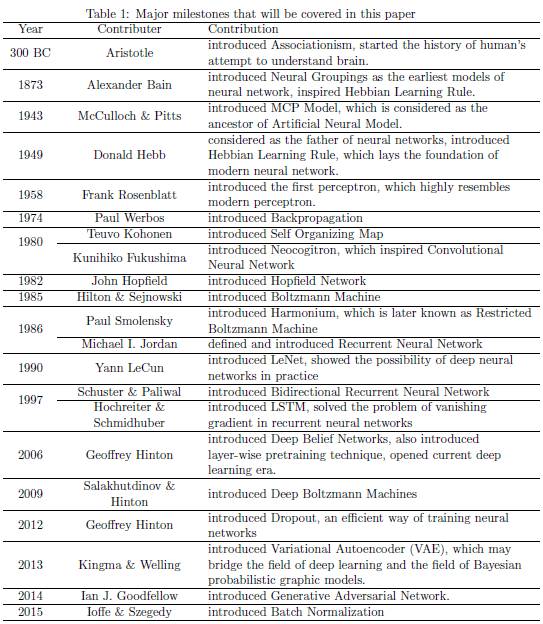
该论文所覆盖的主要里程碑:
-
Aristotle(300BC):提出联结主义,开启了人类试图理解大脑的进程。
-
Alexander Bain(1874):提出了神经群组(Neural Groupings)作为神经网络最早的模型,启发了 Hebbian 学习规则(Hebbian Learning Rule)的构建。
-
McCulloch & Pitts(1943):提出了 MCP 模型,该模型被认为是人工神经模型的原型。
-
Donald Hebb(1949):他被奉为神经网络之父,因为其提出了 Hebbian 学习规则(Hebbian Learning Rule),奠定了现代神经网络的基础。
-
Frank Rosenblatt(1958):率先提出了感知器(perceptron),其非常类似于现代感知器。
-
Paul Werbos(1974):提出反向传播算法。
-
Teuvo Kohonen(1980):提出自组织映射(Self Organizing Map)。
-
Kunihiko Fukushima(1980):提出 Neocogitron,启发了卷积神经网络的构建。
-
John Hopfield(1982):提出了 Hopfield 网络。
-
Hilton & Sejnowski(1985):提出玻尔兹曼机(Boltzmann Machine)。
-
Paul Smolensky(1986):提出 Harmonium,后来被称为受限玻尔兹曼机(Restricted Boltzmann Machine)。
-
Michael I.Jordan(1986):提出并定义了循环神经网络(Recurrent Neural Network)。
-
Yann LeCun(1990):提出 LeNet,展示了深层神经网络实践的可能性。
-
Schuster & Paliwal(1997):提出双向循环神经网络(Bidirectional Recurrent Neural Network)。
-
Hochreiter & Schmidhuber(1997):提出 LSTM,解决了在循环神经网络梯度消失(vanishing gradient)的问题。
-
Geoffrey Hinton(2006):提出深度信念网络(Deep Belief Networks),也引入了逐层预训练技术,开启现在的深度学习时代。
-
Salakhutdinov & Hinton(2009):提出深度玻尔兹曼机。
-
Geoffrey Hinton(2012):提出 Dropout,一种有效的神经网络训练方法。
-
Kingma & Welling(2014):提出变自编码器(Variational Autoencoder /VAE),其是深度学习和贝叶斯概率图形模型的桥梁。
-
Ian J. Goodfellow(2014):提出生成对抗网络(Generative Adversarial Network)。
-
Ioffe & Szegedy(2015):提出批归一化(Batch Normalization)。
本论文的讨论始于在人脑建模上的研究。尽管深度学习今天的成功并不一定是源于其与人脑的相似性(更多是因为其深度的架构),但构建一个模拟大脑的系统的理想确实激励了神经网络的早期发展。因此,接下来一节将从连接主义(connectionism)开始,然后会自然过渡到浅度神经网络成熟的时代。
随着神经网络的成熟,这篇论文继续简要讨论了将浅度神经网络扩展到更深度的网络的必要性,以及深度神经网络所带来的希望和深度架构所带来的挑战。
随着深度神经网络的出现,这篇论文又分成了三个不同的流行主题。具体而言,在第 4 节,论文阐述了深度信念网络以及其构造组件受限玻尔兹曼机(Restricted Boltzmann Machine)作为建模能力和计算负载之间的权衡的演化。在第 5 节,论文关注了卷积神经网络的发展历史,给出了随 ImageNet 比赛而发展的过程中的显著步骤。在第 6 节,论文讨论了循环神经网络及其后继者(如 LSTM、注意模型)的发展和它们的成功。
在对传统的深度学习家族进行过广泛的讨论之后,本论文将继续介绍最近的研究主题,比如变自编码器(VAE)和生成对抗网络(GAN)。这些现代模型通常并没有在神经网络领域的较长的演化历史,而是继承自其它机器学习主题的思想,比如因子分析、概率图模型等等。本论文还解释了这些现代模型和它们的先前思想之前联系,并传递了这样一个思想:尽管我们承认这些模型为深度学习界所带来的巨大贡献,但类似的思想过去已经出现过。
尽管这篇论文主要是讨论深度学习模型,但深度架构的优化也是这个领域不可避免的主题。第 8 节专门给出了一个优化技术的简要总结,包括先进的梯度方法、Dropout、批规范化(Batch Normalization)等。
本论文可以作为 (Schmidhuber, 2015) 的补充材料阅读。Schmidhuber 的论文的目标是指出为现有技术做出了贡献的人,所以他的论文的重点是这一路径上每一个单独的增量成果,因此不能很好地阐述它们每一项。另一方面,我们的论文的目标是为读者提供理解这些模型发展的方式。因此,我们强调的是其中的里程碑并阐述了这些思想,以帮助构建这些思想之间的关联。除了 (Schmidhuber, 2015) 中经典深度学习模型的路径之外,我们还讨论了那些构建于经典线性模型之上的最近的深度学习研究成果。另一篇可做为读者的补充材料的文章是 (Anderson and Rosenfeld, 2000),其中作者们就神经网络的历史这一主题对 90 年代著名的科学领袖进行了广泛的采访调查。
以下为本论文中历史梳理内容的目录:
2. 从亚里士多德到现代人工神经网络(From Aristotle to Modern Artificial Neural Networks)
2.1 联结主义(Associationism)
2.2 Bain 和神经组(Bain and Neural Groupings)
2.3 Hebbian 学习规则(Hebbian Learning Rule)
2.4 Oja 规则和主成分分析器(Oja』s Rule and Principal Component Analyzer)
2.5 MCP 神经模型(MCP Neural Model)
2.6 感知器(Perceptron)
2.7 感知器的线性表征能力(Perceptron』s Linear Representation Power)
3. 从现代神经网络到深度学习时代(From Modern Neural Network to the Era of Deep Learning)
3.1 通用近似属性(Universal Approximation Property)
3.1.1 任何布尔函数的表示(Representation of any Boolean Functions)
3.1.2 连续有界函数逼近解(Approximation of any Bounded Continuous Functions)
3.1.3 任意函数的逼近解(Approximation of Arbitrary Functions)
3.2 深度网络的必要性(The Necessity of Depth)
3.3 反向传播和其特性(Backpropagation and Its Properties)
3.3.1 反向传播寻找线性可分数据的全局最优解(Backpropagation Finds Global Optimal for Linear Separable Data)
3.3.2 线性可分数据的反向传播衰退(Backpropagation Fails for Linear Separable Data)
4. 记忆网络和深度信念网络(The Network as Memory and Deep Belief Nets)
4.1 自组织映射(Self Organizing Map)
4.1.1 学习算法(Learning Algorithm)
4.2.2 Hopfield 网络(Hopfield Network)
4.2.3 学习与推断(Learning and Inference)
4.2.4 能力(Capacity)
4.3 波尔兹曼机(Boltzmann Machine)
4.3.1 玻尔兹曼分布(Boltzmann Distribution)
4.3.2 玻尔兹曼机(Boltzmann Machine)
4.3.3 能量玻尔兹曼机(Energy of Boltzmann Machine)
4.3.4 参数学习(Parameter Learning)
4.4 受限玻尔兹曼机(Restricted Boltzmann Machine)
4.4.1 对照散度(Contrastive Divergence)
4.5 深度信念网络(Deep Belief Nets)
4.5.1 参数学习(Parameter Learning)
4.6 深度波尔兹曼机(Deep Boltzmann Machine)
4.6.1 深度玻尔兹曼机(Deep Boltzmann Machine /DBM)和 深度信念网络(Deep Belief Networks /DBN)
4.7 深度生成模型:现在和未来(Deep Generative Models:Now and the Future)
5. 卷积神经网络和计算机视觉(Convolutional Neural Networks and Vision Problems)
5.1 视觉皮层(Visual Cortex)
5.2 Neocogitron 和视觉皮层(Neocogitron and Visual Cortex)
5.3 卷积神经网络和视觉皮层(Convolutional Neural Network and Visual Cortex)
5.3.1 卷积运算(Convolution Operation)
5.3.2 卷积神经网络和视觉皮层的联系(Connection between CNN and Visual Cortex)
5.4 卷积神经网络的先驱:LeNet(The Pioneer of Convolutional Neural Networks: LeNet)
5.4.1 卷积层(Convolutional Layer)
5.4.2 二次抽样层(Subsampling Layer)
5.4.3 LeNet
5.5 ImageNet 竞赛的里程碑(Milestones in ImageNet Challenge)
5.5.1 AlexNet
5.5.2 VGG
5.5.3 残差网络(Residual Net)
5.6 基本视觉问题的挑战与机遇(Challenges and Chances for Fundamental Vision Problems)
5.6.1 网络的性质与视觉盲点(Network Property and Vision Blindness Spot)
5.6.2 人类标记偏好(Human Labeling Preference)
6. 时间序列数据和循环网络(Time Series Data and Recurrent Networks)
6.1 循环神经网络:Jordan 网络和 Elman 网络(Recurrent Neural Network: Jordan Network and Elman Network)
6.1.1 通过时间的反向传播(Backpropagation through Time)
6.2 双向循环神经网络(Bidirectional Recurrent Neural Network)
6.3 长短期记忆(Long Short-Term Memory)
6.4 注意模型(Attention Models)
6.5 深度 RNN 和 RNN 的未来(Deep RNNs and the future of RNNs)
6.5.1 深度循环神经网络(Deep Recurrent Neural Network)
6.5.2 RNN 的未来(The Future of RNNs)
7. 生成对抗网络和现代架构(Generative Adversarial Networks and Modern Architectures)
7.1 生成对抗网络(Generative Adversarial Networks)
7.1.1 参数学习(Parameter Learning)
7.1.2 GAN 的变体(Variants of GAN)
7.1.3 博弈论和 Minimax(Game Theory and MiniMax)
7.2 变自编码器(Variational Autoencoder)
7.2.1 自编码器(Autoencoder)
7.2.2 VAE
7.3 Select-Additive Networks
7.3.1 线性混合模型(Linear Mixed Model)
7.3.2 Select-Additive Networks
7.4 其它新架构
8. 神经网络的优化(Optimization of Neural Networks)
8.1 梯度方法(Gradient Methods)
8.1.1 Rprop
8.1.2 AdaGrad
8.1.3 AdaDelta
8.1.4 Adam
8.2 Dropout
8.3 批归一化和层归一化(Batch Normalization and Layer Normalization)
8.4「优化」模型架构的优化(Optimization for「Optimal」Model Architecture)
8.4.1 Cascade-Correlation Learning
8.4.2 Tiling Algorithm
8.4.3 Upstart Algorithm
8.4.4 Evolutionary Algorithm
9. 总结
致谢
参考文献
©本文为机器之心编译,
转载请联系本公众号获得授权
。
✄------------------------------------------------
加入机器之心(全职记者/实习生):[email protected]
投稿或寻求报道:[email protected]
广告&商务合作:[email protected]





