你一直在制作的钢铁侠系统遇到了一个棘手的问题，你有多个返回相同状态变量的传感器，你经常听说kalman滤波融合，可是怎么利用kalman进行多传感器的融合呢，之前你了解的kalman知识中并没有涉及。不要着急，这节课将会详细介绍给你。
为了保证在任意高度时刚铁侠系统传感器返回数据具有鲁棒性，你选择了GPS和气压计两款传感器用来返回观察到了高度信息。
所以对于
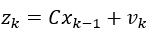的感测方程，有如下的观测模型：
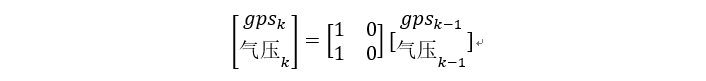
再返回到第一节课的内容，依然按照线性kalman滤波的方程建立算法程序（对照第一节课的5个方程后以下程序），进行测试后得到了很好的传感器融合的效果。
所以线性传感器的多个融合可以通过这个简单的方法，这就是滤波融合的关键，是不是很简单，关键程序如下(假设
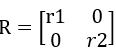,每个传感器个接受500个观测值)
xhat_signal[0] = (z_signal[0][0] +z_signal[1][0]) / 2;
p = 1;
for (k = 1; k < 1000; k++)
{
xhat_signal[k] = xhat_signal[k-1];
p += q;
a = p + r1;
d = p + r2;
e = p / (a*d-p*p);
g1 = e*d - e*p;
g2 = e*a -e*p;
p = (1 - (g1+g2)) * p;
xhat_signal[k] = xhat_signal[k] +g1*(z_signal[0][k]-
xhat_signal[k]) + g2*(z_signal[1][k]-xhat_signal[k]);
}
怎么样，再对照下第一课的公式内容理解下：
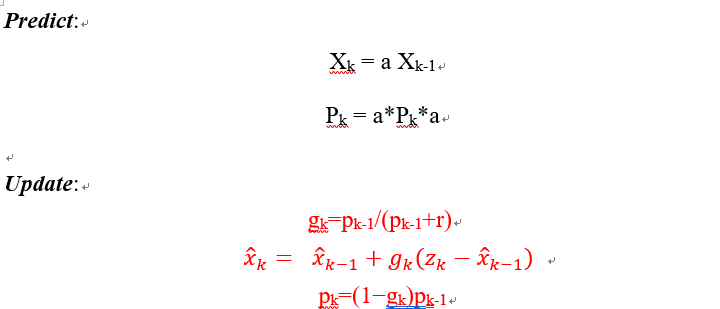
现在你可以很好的解决线性多传感器融合的问题了吧，传感器融合是kalman滤波应用的一个重要领域。在网上搜索kalman滤波会有一个经典的案例—加速度计和角速度计融合，很多人不能很好的理解，因为设计到EKF的知识，在本节课的后面会给大家重点讲解一下，首先让我们继续学习下什么是EKF。
在上一节课中，你和Dsy一同推导了动态系统的估计方法，但是实际系统中有诸多的非线性部分。怎么建立非线性系统的滤波算法，前辈们使用简单的思路将线性kalman扩展到非线性的领域，这种常规的方法被成为EKF（扩展kalman滤波）。
扩展kalman滤波的原理很简单，就是利用泰勒公式将非线性的部分展开成高阶，并去掉高阶项，利用这个线性化技巧将其转化为一个近似的线性滤波问题。
EKF的优点是不必预先计算标称轨迹，但是它只能在滤波误差及预测误差较小时才能使用。
正如介绍的一样，EKF是基于线性kalman的，同样将第一节课介绍的公式改进如下：
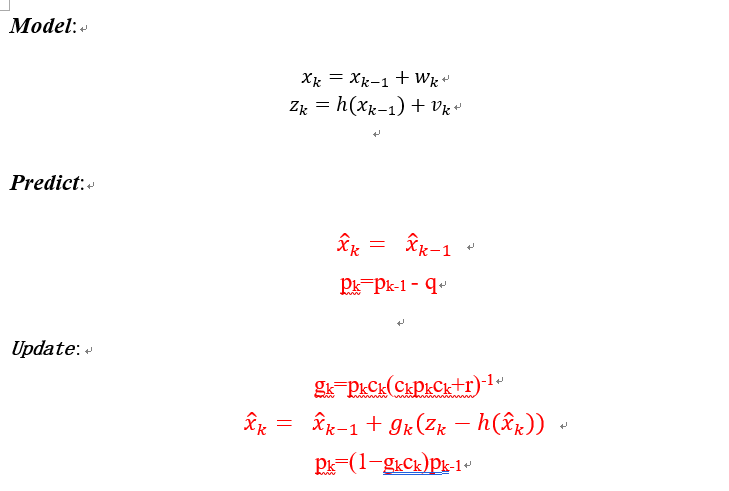
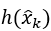和
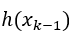是非线性部分，为了方便大家理解，这里去掉了状态转移矩阵。
包含状态转移矩阵的EKF又是怎样的呢，为了说明EKF的问题，我来举个简单的标量系统进行分析。系统的状态方程如果是：
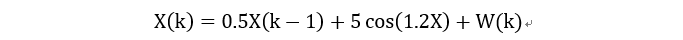
观测方程为：
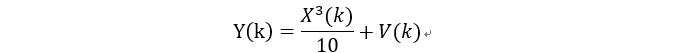
首先要将状态方程一阶线性化，求解状态转移矩阵
。
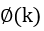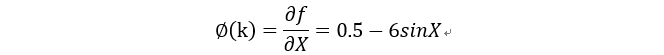然后一阶线性化观测矩阵H(k):
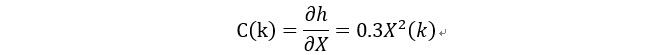
同样，如果状态方程和感测矩阵不是一维的，就要用雅克比矩阵来线性化，其实原理是一样的，雅克比矩阵只不过是线性代数中的一种多元函数求导的方法。
总结下EKF的处理过程可以归纳为以下几步：
第一步：一阶线性化状态方程，求解状态转移矩阵；
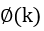第二步：阶线性化观测矩阵，求解观测矩阵C(k)；
第三步：求协方差矩阵预测P(k|k-1)：
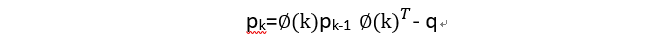
第四步：求Kalman滤波增益：
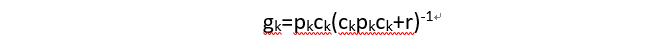
第五步：求状态更新：
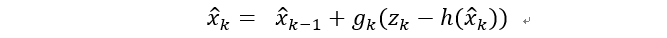
第六步：协方差更新：
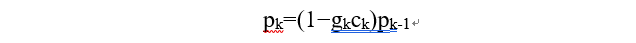
以上六步为EKF的一个计算周期，也是最经典的EKF处理过程。
将公式直接转换成程序就实现了EKF的应用，你依然想了解其中的数学推演，这部分内容其实很简单，最关键的推演核心在于通过已知的概率密度函数P(X,Kt)，获得一个实际的估计算法，EKF的方案就是通过泰勒级数展开公式线性化获得当前状态向量的估计。Dsy告诉你，EKF总结成一句话就是通过把你的非线性控制模型在雅克比空间的小范围内线性化，然后再利用线性卡尔曼滤波的方法进行滤波。所以这部分数学方法的推演其实和线性kalman的内容很相似，看一下前几节课的内容自行推导吧，很简单。
既然已经学习了EKF和多传感器融合的知识，我们来看一个EKF传感器数据融合的例子。这部分我就不开脑洞编例子了，直接拿斯坦福大学Gordon的一个6 DOF IMU Sensor Fusion Euler Angles（6维度的传感器融合）例子。
首先是模型的状态空间如下：
EKF—— IMU Euler Angles
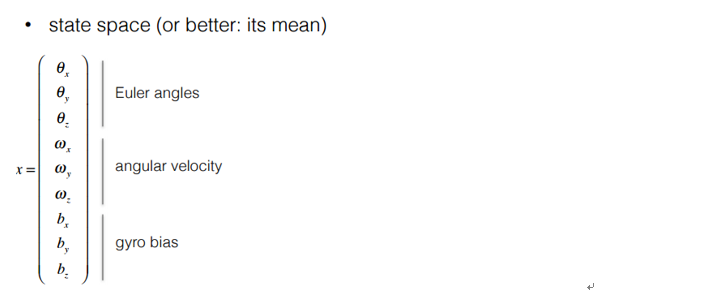
此次建立系统状态模型，如下：
接下来确定误差协方差矩阵：
接下来让我们确立下观测模型：
接下来就是非线性部分了：
通过观察我们发下，其实本模型中只有观察模型是非线性的。所以之前教给大家的EKF处理步骤的第一步就没有啦，直接从第二步开始，求解C(k):
这里的
就是我们的C(k)，其余的部分再按照后续的EKF过程进行求解就好了，有了这部分的理论支持，是不是看相似的滤波融合的例子都so easy了呢，哈哈，继续加油，下节课Dsy还会来教你EKF的应用，告诉你他正在做的导弹制导中的EKF，国防领域的核心算法，是不是很期待，消化了这节课就去看下节课吧，继续加油。
Advanced IMU Sensor Fusion with Kalman Filtering(GordonWetzstein—Stanford University)
长按下图，识别图中二维码，关注“泡泡机器人SLAM”（ID：paopaorobot_slam）公众号。系列全文PDF下载链接在【泡泡机器人原创专栏】第 5 课 UKF 与粒子滤波实现中给出，敬请关注。
【版权声明】泡泡机器人SLAM的所有文章全部由泡泡机器人的成员花费大量心血制作而成的原创内容，希望大家珍惜我们的劳动成果，转载请务必注明出自【泡泡机器人SLAM】微信公众号，否则侵权必究！同时，我们也欢迎各位转载到自己的朋友圈，让更多的人能进入到SLAM这个领域中，让我们共同为推进中国的SLAM事业而努力！
【注】商业转载请联系刘富强（[email protected]）进行授权。普通个人转载，请保留版权声明，并且在文章下方放上“泡泡机器人SLAM”微信公众账号的二维码即可。
【编辑】徐武民
