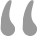
生信草堂

将会与更多的优秀微信公众号合作，把最优秀的微信推文呈现给大家，希望可以帮助读者更多的了解生信技术，培养和提高读者的生信分析能力！

号外，号外，号外

你想和生信分析大神做好朋友么？

你想认识更多爱好生信分析的小伙伴么？

你想让自己的生信分析走上快车道么？

那就赶快加入我们的生信交流微信群吧！

正确加入我们的模式是：

添加我们的微信bioinformatics88为好友

标注“加入生信草堂交流群”

在群里请大家注明自己本名，单位，研究领域

便于小编管理

写在前面

优秀的作品都有三部分曲，如骇客帝国、教父、指环王等。

扩增子系列课程也分为三部曲：

第一部《扩增子图表解读》：加速大家对同行文章的解读能力。

第二部《扩增子分析解读》：学习数据分析的基本思路和流程。

第三部《扩增子统计绘图》：即是对结果进行可视和统计检验，达到出版级的图表结果。

本部分练习所需文件位于百度网盘，链接：http://pan.baidu.com/s/1hs1PXcw 密码：y33d。

绘图和统计全部为R语言，建议复制代码，在Rstuido中运行，并设置工作目录为存储之前分析结果文件的result目录。

主坐标轴分析(PCoA)展示所有样品间的最大差异

采用PCoA展示样品间的最大差异，代码以bray_curtis为例，其它距离只需替换为weighted_unifrac,unweighted_unifrac即可。

# 运行前，请在Rstudio中菜单栏选择“Session - Set work directory -- Choose directory”，弹窗选择之前分析目录中的result文件夹

# 安装相关软件包，如果末安装改为TRUE运行即可安装
if (FALSE){
  source("https://bioconductor.org/biocLite.R")
  biocLite(c("ggplot2","vegan"))
}

# 加载相关软件包
library("ggplot2")
library("vegan")

# 读入实验设计
design = read.table("design.txt", header=T, row.names= 1, sep="\t") 

# 读入bray_curtis的距离矩阵
bray_curtis = read.table("beta/bray_curtis_otu_table_css.txt", sep="\t", header=T, check.names=F)

# 过滤数据并排序
idx = rownames(design) %in% colnames(bray_curtis) 
sub_design = design[idx,]
bray_curtis = bray_curtis[rownames(sub_design), rownames(sub_design)] # subset and reorder distance matrix

# 将距离矩阵进行主坐标轴分析
pcoa = cmdscale(bray_curtis, k=3, eig=T) # k is dimension, 3 is recommended; eig is eigenvalues
points = as.data.frame(pcoa$points) # get coordinate string, format to dataframme
colnames(points) = c("x", "y", "z") 
eig = pcoa$eig
points = cbind(points, sub_design[match(rownames(points), rownames(sub_design)), ])

# 绘制主标准轴的第1，2轴
p = ggplot(points, aes(x=x, y=y, color=genotype)) +
  geom_point(alpha=.7, size=2) + 
  labs(x=paste("PCoA 1 (", format(100 * eig[1] / sum(eig), digits=4), "%)", sep=""),
       y=paste("PCoA 2 (", format(100 * eig[2] / sum(eig), digits=4), "%)", sep=""),
       title="bray_curtis PCoA")
p
ggsave("beta_pcoa_bray_curtis.pdf", p, width = 5, height = 3)
ggsave("beta_pcoa_bray_curtis.png", p, width = 5, height = 3)

以下有详细的图片讲解
图中WT和OE在第一轴明显分开的，但WT与KO间区分不明显，是否存在显著差别呢。

我们以WT和OE为例，统计组间是否存在显著差异。

# 统计WT与KO间是否有差异显著
# 取两组实验设计子集
design2 = subset(sub_design, genotype %in% c("WT","KO"))
# 获取对应的子距离矩阵并排序
sub_dis_table = bray_curtis[rownames(design2),rownames(design2)]
# 计算距离矩阵
sub_dis_table F)`[1]
# 显示组间的pvalue值
adonis_pvalue

pvalue值结果不是一个确定的值，是多次统计的结果，但差别不大，每次大约为0.01左右，即WT与OE存在显著差异，但还是不极显著。读者可以自行计算WT与OE试试，看看P值有多显著。

限制条件主坐标轴分析(CCA)展示组间的最大差异

通常PCoA展示的是所有样品间的最大差异，而实验中想要找的是组间的差异，就需要限制条件的主坐标轴分析。

# CCA分析功能函数
variability_table = function(cca){
  chi = c(cca$tot.chi, cca$CCA$tot.chi, cca$CA$tot.chi)
  variability_table = cbind(chi, chi/chi[1])
  colnames(variability_table) = c("inertia", "proportion")
  rownames(variability_table) = c("total", "constrained", "unconstrained")
  return(variability_table)
}

# 读入CSS标准化的OTU表，并与实验设计比对筛选和数据重排
otu_table = read.table("otu_table_css.txt", sep="\t", header=T, row.names= 1) # CSS norm otu table
idx = rownames(sub_design) %in% colnames(otu_table) 
sub_design = sub_design[idx,]
sub_otu_table = otu_table[, rownames(sub_design)] 

# Constrained analysis OTU table by genotype
capscale.gen = capscale(t(sub_otu_table) ~ genotype, data=sub_design, add=F, sqrt.dist=T, distance="bray") 

# ANOVA-like permutation analysis
perm_anova.gen = anova.cca(capscale.gen)

# generate variability tables and calculate confidence intervals for the variance
var_tbl.gen = variability_table(capscale.gen)
eig = capscale.gen$CCA$eig
variance = var_tbl.gen["constrained", "proportion"]
p.val = perm_anova.gen[1, 4]

# extract the weighted average (sample) scores
points = capscale.gen$CCA$wa[, 1:2]
points = as.data.frame(points)
colnames(points) = c("x", "y")
points = cbind(points, sub_design[match(rownames(points), rownames(sub_design)),])

# plot CPCo 1 and 2
p = ggplot(points, aes(x=x, y=y, color=genotype)) +
  geom_point(alpha=.7, size=1.5) +
  labs(x=paste("CPCoA 1 (", format(100 * eig[1] / sum(eig), digits=4), "%)", sep=""),
       y=paste("CPCoA 2 (", format(100 * eig[2] / sum(eig), digits=4), "%)", sep="")) + 
  ggtitle(paste(format(100 * variance, digits=3), " % of variance; p=",format(p.val, digits=2),sep="")) 
p
ggsave(paste( "CPCoA.pdf", sep=""), p, width = 5, height = 3)
ggsave(paste( "CPCoA.png", sep=""), p, width = 5, height = 3)

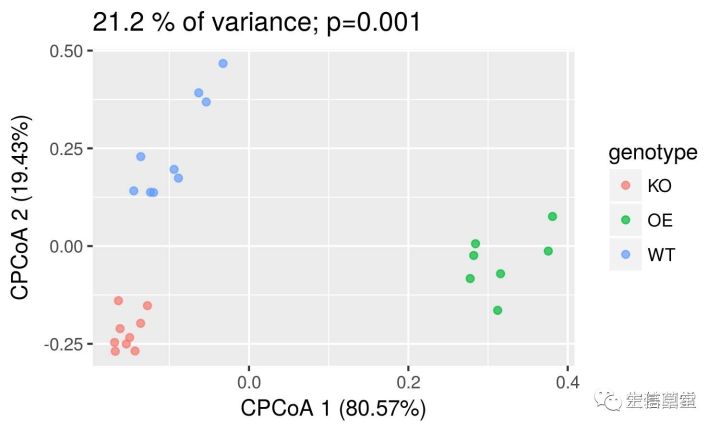
图中三个组能明显分开，代表组间存在一致的差异。顶部展示21.2%表示组间的差异占总体的比例，p=0.001表示组间有显著差异。两轴百分比是此平面下可解释差异的百分比。

以下是详细的图片讲解

散点图

数据点在直角坐标系平面上的分布图。A scatter plot (also called a scatter graph, scatter chart, scattergram, or scatter diagram) is a type of plot or mathematical diagram using Cartesian coordinates to display values for typically two variables for a set of data.
在宏基因组领域，散点图常用于展示样品组间的Beta多样性，常用的分析方法有主成分分析(PCA)，主坐标轴分析(PCoA/MDS)和限制条件的主坐标轴分析(CPCoA/CCA/RDA)。

Beta多样性

Beat多样性是生态学概念，专指不同组或生态位间物种组成的差异。详见Wiki

分析方法

在读文章中经常可以看到PCA分析、PCoA分析，NMDS分析，CCA分析，RDA分析。它们在本质上是排序(ordination)分析。排序的过程就是在一个可视化的低维空间(通常是二维)重新排列这些样品，使得样方之间的距离最大程度地反映出平面散点图内样品间的关系信息。常用的排序方法如下：

1、只使用物种组成数据的排序称作非限制性排序(unconstrained ordination)  

即无限制条件，只找所有样品间的最大差异的投影平面，主要方法如下：

1. 主成分分析(principal components analysis,PCA)是一种常用的数据间差异分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征向量，常用于高维数据的降维。原理推荐阅读PCA的数学原理。

2. 对应分析(correspondence analysis, CA)

3. 去趋势对应分析(Detrended correspondence analysis, DCA)

4. 主坐标分析(principal coordinate analysis, PCoA)

5. 非度量多维尺度分析(non-metric multi-dimensional scaling, NMDS)
   在非限制性排序中，分析种类很多，但原理相近。16S和宏基因组数据分析通常用到的是PCA分析和PCoA。原理有时间可以细读，但至少知道是用坐标间距离来反应样品间差异大小即可。
   PCA和PCoA分析的区别：PCA分析是基于原始的物种组成矩阵所做的排序分析，而PCoA分析则是基于由物种组成计算得到的距离矩阵得出的。

2、同时使用物种和相关环境因子组成数据的排序叫作限制性排序(constrained ordination)
即寻找某一条件下，可最大限制解释这一条件的投影平面。条件可以为连续(温度、湿度、pH值、各种土壤理化性质等)或非连续的变量(如人为分组、基因型、地理位置、取样时间、实验批次等)。常分析方法有：

1. 冗余分析(redundancy analysis,RDA)

2. 典范对应分析(canonical correspondence analysis, CCA)。
   此类方法可以计算某一条件下，各组间是否存在显著差异，并且可以计算出该条件下平面展示的差异占样品间总体差异的比例。
   RDA或CCA的区别：RDA是基于线性模型，CCA是基于单峰模型。一般我们会选择CCA来做直接梯度分析。但是如果CCA排序的效果不太好，就可以考虑是不是用RDA分析。RDA或CCA选择原则：先用species-sample资料做RDA分析，看分析结果中Lengths of gradient 的第一轴的大小，如果大于4.0，就应该选CCA，如果3.0-4.0之间，选RDA和CCA均可，如果小于3.0, RDA的结果要好于CCA。

距离计算方法

样品两两间的距离计算方法也有多种方法，大家都应该听过Euclidean(欧几里德)吧，即有非常有名的欧氏距离(Euclidean distance)。在生物学研究中，主要分为两大类，一种是物种距离(如常用Jaccard，Bray-Curtis)；另一种是基于进化的距离(Unifrac),基于进化的距离还包含权重(Weighted)和非权重(Unweight)两种。
在选择上，我习惯用Bray-Curtis距离，是因为这种方法在我研究的方面有比较好的结果。习惯上我是每种距离都做分析，那种能更好的解释科学问题就用那种。

看图实战(Result)

示例1. 非限制条件的PCoA

Edwards, J., et al. (2015). PNAS Fig. 1C
这篇文章分析了水稻根不同区域的细菌组成，16S分析文章较系统的作品，两年被引用147次，推荐阅读。

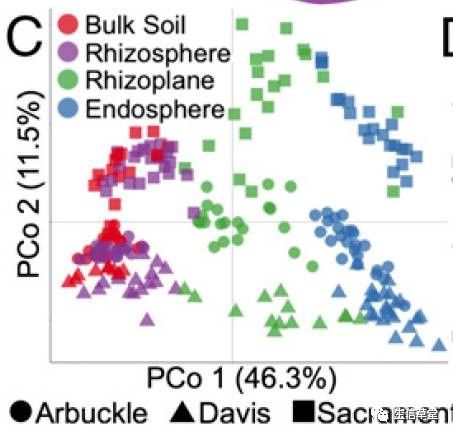
图1.C 主坐标轴分析(PCoA)展示样品间差异(Beta diversity)，距离计算方法采用Weight Unifrac。

1. 图中元素解释

• X轴标签PCo 1 (46.3%)代表能最大区分所有样品的第一主坐标轴，可以解释样品中所有差异的46.3%；

• Y轴标签PCo 2 (11.5%)代表能最大区分所有样品的第二主坐标轴，可以解释样品中所有差异的11.5%；仅这两轴形成的第一个平面，即展示了样品间一半以上的差异；

• 下部形状图例(实心圆Arbuckle、三角Davis、正方形Sacaramen)对应的是地名，用以区分图中不同地区的材料；

• 左上角颜色图例，用以区分不同取材部位(compartment)；

1. 图表结果：图中展示在最大解释率的第一坐标轴，不同颜色表示的取样部分可以很好的区分开，即样品间的差异主要是由于样品的来源不同决定的；同时不同形状代表的不同地区可以在第二坐标轴上可以较好的区分，表明不同地理位置对微生物组有影响，并且影响远小于不同取样部位；

2. 图观察规律或结论：植物根部特定的区域(不同取样来源)存在微生物组的差别，而且是最主要的差别，可很好的由第一坐标轴解释；不同地区土壤环境因素下根际微生物组也是明显不同的，是整体实验中第二大差异贡献原因，可以很好的在第二坐轴上区分开。

3. 经验和技巧：通常我们的实验设计和想要找的差异，根据预期的差异大小很可能与主坐标轴分开规律相一致，是因为我们的实验设计合理且有针对性(Common sense)；颜色和形状的标注建议：因为人类对不同颜色的散点分布比较容易区分，故将最重要的发现用颜色标示，便于观察，可将第二关注的因素按形状标注；对于实验组大于7组时，颜色太多相近很难区分时，可以每组样品均标为不同颜色和形状来进一步对组进行区分。

附图注原文：
(B) PCoA using the WUF metric indicates that the largest separation between microbial communities is spatial proximity to the root (PCo 1) and the second largest source of variation is soil type (PCo 2)

示例2. 以取材部位和基因型为条件的主坐标轴分析(CPCoA/CCA)

Zgadzaj, R., et.al., 2016 .PNAS 
这篇文章分析了百脉根根瘤的微生物组成，同时在根瘤缺失突变体条件下发现根和根际微生物均有较大差异的变化。

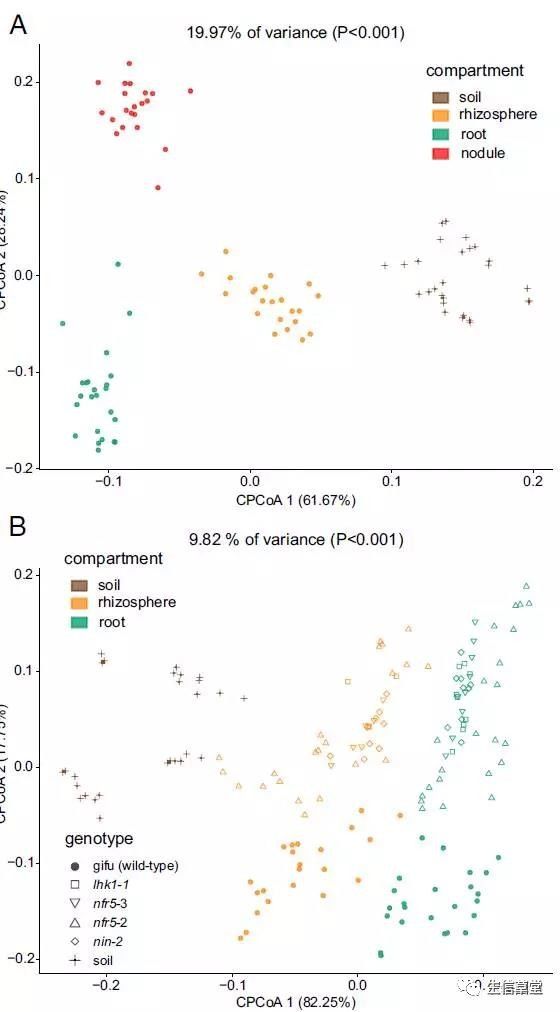
图2. 散点图展示限制性主坐标轴分析(Constrained PCoA/ CCA)取材部位和基因型间的差异。

1. (A) 采用CCA方法结合bray-curtis距离，分析以取样部分(compartment)条件下可显示各组最大差异投影平面；图顶部19.97% of variance (P<0.001)表示当前所展示的平面坐标系，可解释所有样品间总差异的19.97%的(另一种我的解读是当前条件对样品间总差异的贡献率为19.97%，即导致差异所占的权重)，并且各组间存在显著差异(P<0.001)；

2. (B) 以基因型为条件分析最大解释基因型组间差异的空间平面，可解释9.82%的变异，并且有显著差异，其中作者按形状标出了各基因型；同时作者还按compartment进行着色，在这一平面上，compartment仍能很好的分开。

3. 图表结果：Compartment可解释19.97%差异，且区分明显；突变体与WT(gifu)可以区分，区分不大(占9.82%变异中的17.75%的纵轴上可区分)；各突变体间很难区分，完全混在一起；在基因型最大解释平面上，compartment仍能非常好的在第一轴上区分。

4. 图表结论或规律：Compartment对微生物组成影响较大，基因型其次；不同根瘤突变体差异极小。

5. 图片优点：配色选择各组区分较好，不同图配色方案一致；图片使用矢量图线条和文字清楚(上面介绍水稻的文章全是位图，经过PDF的压缩，文字非常模糊)。个人建议，只要不是照片，画的图都用矢量，无极缩放不失真，一般体积还小，而且方便编辑修改。

附图注原文：
Fig. 2. (A) Constrained PCoA plot of Bray–Curtis distances between samples including only the WT constrained by compartment (19.97% of variance, P > 0.001; n = 94). (B) Constrained PCoA plot of Bray–Curtis distances constrained by genotype (9.82% of variance explained, P < 0.001; n = 164). Each point corresponds to a different sample colored by compartment, and each host genotype is represented by a different shape. The percentage of variation indicated in each axis corresponds to the fraction of the total variance explained by the projection.

Reference

1. https://en.wikipedia.org/wiki/Scatter_plot

2. https://en.wikipedia.org/wiki/Beta_diversity

3. PCA的数学原理 http://blog.csdn.net/xiaojidan2011/article/details/11595869

4. PCA、PCoA、NMDS、CCA、RDA傻傻分不清楚 http://www.dxy.cn/bbs/topic/32534684

5. Edwards, J., et al. (2015). “Structure, variation, and assembly of the root-associated microbiomes of rice.” Proceedings of the National Academy of Sciences 112(8): E911-E920.

6. Zgadzaj, R., Garrido-Oter, R., Jensen, D.B., Koprivova, A., Schulze-Lefert, P. and Radutoiu, S., 2016. Root nodule symbiosis in Lotus japonicus drives the establishment of distinctive rhizosphere, root, and nodule bacterial communities. Proceedings of the National Academy of Sciences, 113(49), pp.E7996-E8005.

7. http://blog.csdn.net/woodcorpse/article/details/73979100

学术手拉手