编辑:Gemini
提到数学家,可能许多读者脑海中浮现的第一帧画面是这样的:

图片来自"The hundred greatest mathematicians of the past"
尽管来自于不同时代,说着不同的语言,头发和胡子数量也有巨大差异,每张照片里面却都凝聚着同样伟大的智慧,同样深邃的思想。数学的半壁江山浓缩在一张三寸不足的泛黄纸片上,大道至简,令人惊叹不已;藏诸塌侧,半月三旬后再度翻看,又令人回味无穷。
然而美中不足之处在于,以上名单(可搜索"The hundred greatest mathematicians of the past")主要考虑对象是在纯数学领域有重大影响的人物,很多伟大的应用数学家,例如费希尔(现代数理统计和生物数学的奠基者)、香农(信息学之父)、维纳(控制论之父)和伊藤清(随机微分方程的提出者,对金融领域产生颠覆性影响)等则未能出现在这个榜单中(唯有冯诺依曼和阿兰图灵这两位全才例外)。事实上这些应用数学家对整个科学界的影响是极为巨大的,只不过往往被纯数学家们的光辉掩盖住了。
笔者的目的,便是通过介绍牛津大学的一个应用数学团队,让读者们对应用领域的数学家们有所认识,让这些被掩盖住的光辉重见天日。
第一部分 牛津大学生物数学中心
笔者曾和一位本系(数学系)的东欧小哥讨论过欧美学术界的异同。当谈到生物数学(笔者的主要研究方向)时,小哥信誓旦旦地说:“生物数学?!欧洲可没多少人做这个!”
看来要让生物数学这话足足让我扫兴了一个星期。然而一星期后笔者就收到了牛顿研究所一个生物数学会议的邀请通知:

牛顿研究所位于英国的剑桥大学,这说明生物数学在欧洲还是相当有关注度的!正欲兴致勃勃地用这封邮件同东欧小哥辩论,而当看到小哥一米九的高大身材,笔者倒吸一口凉气;逡巡良久,只好偷偷地把邮件藏到垃圾箱,把一切人证物证烂熟在心中。

事实上在后来的生物数学会议中,笔者又注意到了不少来自英国、法国和德国的专家与会,说明生物数学的光辉已经逐渐扩散到整个欧洲了。东欧数学家自成体系,也许生物数学这一新兴“物种”尚未攻破他们的免疫防线。
生物数学在英国还是人气颇高的。除了剑桥大学牛顿研究所旗下的生物数学研究院,牛津大学也有一个“沃夫森生物数学中心”(Wolfson Center for Mathematical Biology)。这个中心的头目叫Philip Maini,是爱尔兰生物数学家[1]:

Philip Maini, 图片来自维基百科
Maini在整个应用数学界都非常活跃,可以是这几十年来全球应用数学的发展的见证者。笔者曾在三个不同报告厅见到过Maini,每个报告厅都被这位头发花白的数学家装裱地生机盎然,宛如岑参笔下一夜间被春风唤醒的千万簇梨花——他的演示文稿并没有繁多的文字或复杂的数学公式,但听众们总能在他抑扬顿挫的语调中心潮暗涌:或领悟到数学与其他学科之间的千丝万缕,或体会到潜伏在简单公式中的伟大智慧,或摸索出简朴文稿背后鲜为人知的试验探索。三言两语便诱出千思万绪,“大师”这两字在这里得到最佳诠释。
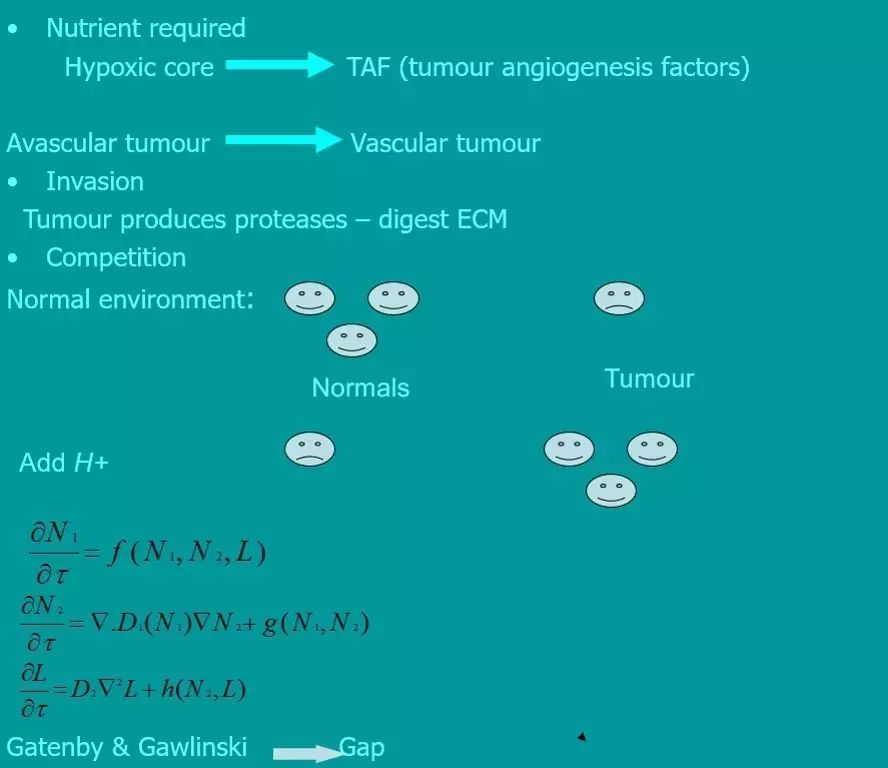
Maini的演示文稿。唯一的槽点大概在于文稿背景色稍微丑了些
笔者私下请教过Maini一些问题。第一次和全球顶尖的应用数学家交谈总是免不了几分羞涩,而Maini则不断鼓励我“There are no silly questions.”(不存在愚蠢的问题)。当笔者提出自己的一个简单想法时,他会像激动地喊道:“我怎么没想到这个!”如同小孩子找到了新的玩具。这种返璞归真的沟通方式,让笔者备受鼓舞。
第二部分 形态发生(Morphogenesis)
那么沃夫森生物数学中心的数学家们平常都在研究什么呢?我们可以从Maini的研究列表中得到线索(为方便大家理解,笔者对这些研究方向进行了意译):

图片来自Maini的个人主页[2]
这些研究方向看似五花八门,但基于的数学模型主要有三个:
1. 连续力学模型(描述物体在弹性介质和流体中的运动)[3]
2. 细胞的趋性模型(趋药性、趋光性等)[4]
3. 图灵模型(生物图案的生成者)[5]
以上每个模型都对应着一类方程,称作耗散结构方程(Dispersive equation)。这一类方程依赖于时间“t”和空间坐标“x”,之所以叫做“耗散结构”,是因为系统的“能量”会随着时间的推移而逐渐减小,熵增原理便是耗散结构方程的一个特例。在数学上,耗散结构方程(尽管这个术语不是数学家发明的)拥有数不清道不尽的神奇特性,所以今天我们在不同论文中看到的同时间“t”有关的偏微分方程,几乎都是耗散结构方程。
本文中笔者将着重介绍图灵模型。在此之前,我们先来瞻仰瞻仰图灵这一位大帅哥:

阿兰·图灵。图片源自网络
或许图灵最广为人知的是他在计算机智能领域的贡献(例如图灵测试)。事实上他引用量最大的论文叫做“形态发生的化学基础”(The chemical basis of morphogenesis)[5]。形态发生是一个非常广泛的生物概念,这个概念包括了细胞分化、胚胎形成、器官形成、肿瘤扩散以及生物表面花纹的形成等。我们容易想到,形态发生是基于一系列复杂的化学反应,而图灵的工作,则是把这些化学反应总结成为一个简单的微分方程组:

或许读者们已经在笔者的其他文章中看到过这个方程了[6-8]。多一分邂逅便少几分朦胧与暧昧,相信这个方程的再度出现能让读者更加体会到耗散结构方程在整个自然科学界的核心地位。笔者写了一段代码(用python,有兴趣的读者可参考[9])用以模拟一个简单的图灵模型:

是不是很像猎豹毛皮上的花纹?
值得一特的是,图灵模型并非唯一研究生物图案的数学方程。物理学家们更偏向于应用复Ginzburg-landau方程(最早用于描述超导现象)和Cahn-Hilliard方程(最早用于描述二元体,如水和酒精的分离)。尽管这两个方程的推导是从能量角度出发的,和图灵的推导方式全然不同,但从形式上看来,这些方程具有惊人的相似性,可谓英雄所见略同。这一点笔者会在以后继续详细解读。
第三部分 科普工作
笔者随后发现,Maini所掌管的生物数学中心还经常做一些科普性的工作,尤其是该中心的研究员Thomas Woolley。作为热衷于把复杂的数学理论散步于大众的青年科学家(目测35岁左右),Woolley身上不仅沿袭了沃夫森数学中心所特有的激情洋溢,而且形成了自己的独立风格。他的演示文稿主要由五彩斑斓的图片构成(不得不承认比Maini的文稿颜值高出不少),以致于听完他的报告后,听众们很难相信他其实是数学家。而当Woolley把他的演示文稿发给笔者时,只能通过云端传送,因为他的文稿实在太占空间了,邮箱附件难以容下这样的大气。
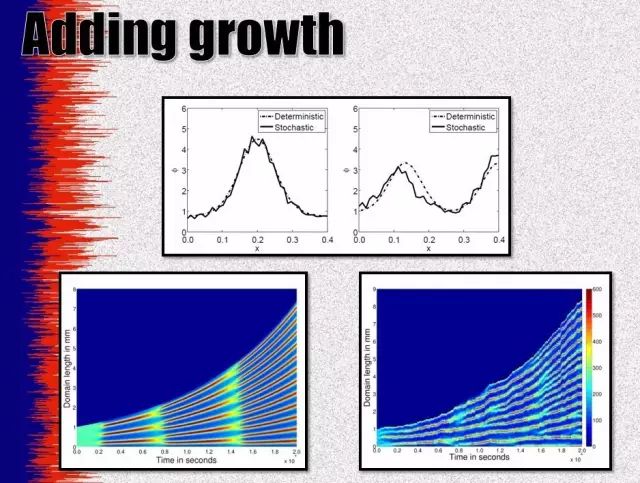
Woolley的演示文稿几乎都是这个画风
Woolley对科研的热情同样延续到了他的生活中。他是媒体的常客,常常受BBC邀请录制一些轻松有趣同时不乏科学严谨的节目,链接[11]给出了Woolley的视频目录。与此同时,Woolley也常常在他的学术报告中分享自己的“失败”经历,例如得到的数值模拟结果如何与实验前的预想不同等等。这一风格对笔者本人的影响是巨大的,或许这也正是为什么Woolley的学术报告能受到众多学者青睐的原因。
当知晓笔者也在做类似的科普工作后,Woolley显得更加兴奋。他和Maini等人之前写过一篇关于僵尸的数学模型[12](被登上过泰晤士报),与笔者之前写过的《星际争霸》[7]一文颇为相似,于是我们谈论了很长时间的星际争霸(当然笔者之前写的只是上半部分)。我们都对单机对战时的神族狂剑客一波流(Zealot rush)感到头疼。
当晚Woolley就给笔者发送了另一篇他自己创作的科普文,题目为《光怪陆离的生物形态》[13](Mighty Morphogenesis,笔者的翻译),希望笔者能翻译成中文。
然而文章写到这里,笔者回眸一看,发现本文已经覆盖了[13]的大部分内容。因此限于篇幅,笔者不再重复翻译,而只是简要总结一下[13]中的新内容。有兴趣的读者可以阅读原文:
《光怪陆离的生物形态》中的特色内容:
1. 图灵晚年因同性恋入狱,后卒于氰化物中毒,享年42岁不到。
2. 如果不加上扩散项,图灵模型是不会产生图案的。所以图灵模型产生的图案又叫做“扩散引起的不稳定”(Diffusion-driven instability)。
3. 图灵图案到底会产生斑点还是条纹?这和表面积大小有关。如下图所示:

表面积的增加可能使条纹裂变成斑点。b为Woolley大学时期照片(现在似乎胖了些)
4.从某种角度看来,图灵的论文[5]是发展生物学界有史以来最为重要的文章,因为它彻底颠覆了许多实验学家的思维模式(具体说来,热力学第二定律被彻底改写,因为图灵去世六年后,违反熵增原理的化学反应,BZ反应[13]被化学家发现。而这类反应正是图灵通过他的模型所预言存在的——笔者注)。
第四部分 总结
也许读者们已经清晰地感受到,大师其实离我们并不遥远。并非所有数学界的大师都是板着一副面孔的,相反,他们很乐意传递自己的所见所闻,很愿意和不同背景的人们交流。而笔者和他们的交流,更多像是平辈之间的相互探讨,或许这种探讨更有助于思维的对冲碰撞和新想法的横空出世。这和笔者“严谨而不拘谨”[14]的科研观点颇为相似。
应用数学家们善于把数学融入生活的方方面面。也许正是因为太过“通俗”,他们对世界的影响往往容易被人们所忽视。笔者也希望通过本文,让更多读者了解到应用数学家们不可磨灭的贡献,同时希望让大家知道,数学的趣味性不仅仅局限于数论、组合、代数方程等;它的渗透力之强,扩散范围之广,早已隐含在生活中的方方面面。
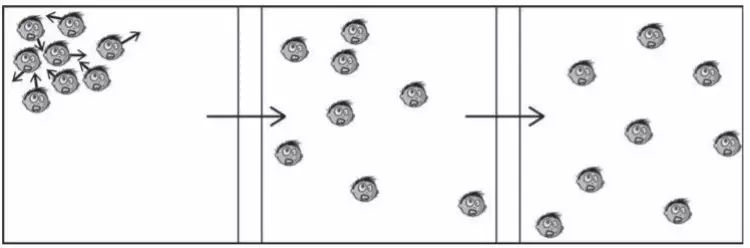
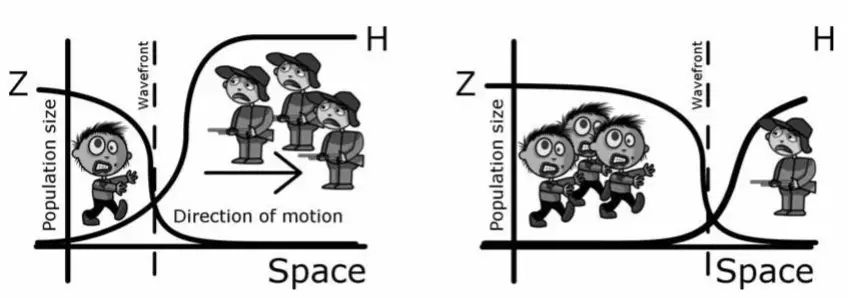
最后引用《僵尸的数学模型》[12]一文中的两张图。读者们可以猜一猜,如何用数学语言描述僵尸的活动过程呢?
参考文献:
[1] https://en.wikipedia.org/wiki/Philip_Maini
[2] https://people.maths.ox.ac.uk/maini/
[3] P. Maini et. al, Sequential pattern formation in a model for skin morphogenesis.
[4] E. Keller, Model for Chemotaxis.
[5] A. Turing, The chemical basis of morphogenesis.
[6] https://mp.weixin.qq.com/s?__biz=MzIyNjc2NzY4OA==&mid=2247483706&idx=1&sn=1a920ef867db8e3d4642c619f764f04d&chksm=e86a271ddf1dae0b308ef4b559b9a266b8a851faa9dcaf3c04285a5a950c2c83a5ef706f94bc#rd
[7] https://mp.weixin.qq.com/s?__biz=MzIyNjc2NzY4OA==&mid=2247483777&idx=1&sn=27ec78f138b1fa74d81a6fdf7c712976&chksm=e86a27a6df1daeb03c1265a2d88a4f0c466b3de2b2ddacf17dfa6a427582ff0bc55e7d7cee8a#rd
[8] https://mp.weixin.qq.com/s?__biz=MzIyNjc2NzY4OA==&mid=2247483922&idx=1&sn=25db02958d8481038fa4391bc92cc08a&chksm=e86a2435df1dad23914f157915bd66ffd5c8af0ea08bd2e02cea57d2a3447c0757d27555a9af#rd
[9] https://people.math.osu.edu/yang.2677/Turning.txt
[10] http://people.maths.ox.ac.uk/woolley/outreach.html
[11] http://people.maths.ox.ac.uk/woolley/outreach.html
[12] T. Woolley et. al, Mathematical Modelling of Zombies.
[13] https://en.wikipedia.org/wiki/Belousov%E2%80%93Zhabotinsky_reaction
[14] https://mp.weixin.qq.com/s?__biz=MzIyNjc2NzY4OA==&mid=2247483977&idx=1&sn=9c04fb2eb29c96b0f741bf83d5d743f4&chksm=e86a246edf1dad78aab171359ef6cc592e67c7ca4407a37f6546edb971f7b087bb9cfd1835f8#rd
往期经典文章回顾
高等数学、线性代数、概率论与数理统计、几何学这些知识可以用来干什么?主要应用有哪些?
线性代数的本质--对线性空间、向量和矩阵的直觉描述
理解矩阵背后的现实意义
数学系和物理系学生有什么差别?
线性代数的本质
Leibniz 如何想出微积分?(三)
PCA的数学原理
零除以零在数学中有意义吗?
算法|人人都该了解的十大算法
对傅里叶级数的理解











