【点击】 加入大模型技术交流群

原文：https://zhuanlan.zhihu.com/p/619511222

压缩即智能？

最近在研究 OpenAI 发现，他们其实做的只是机器学习的第一原理，也是机器学习的终局： 优化对于未来观察的无损传输的压缩大小 。进一步分析后发现，这个理论非常 powerful，因为仅仅如此，便能通向超过人类的智能 （Super-human Intelligence）。本文会介绍无损压缩的基本原理和具体实现以及对于 AI 未来发展的猜想。

在和小伙伴一起研究的过程中，引出一些有意思的讨论。虽然由于篇幅限制不会特别深入，但希望能引起大家的兴趣。讲无损压缩的部分为了保持 self-contained 的阅读体验，正文里尽量没有引用资料；参考文献会在最后一起给出。对模型训练的无损压缩解释有了解的同学，也可以直接跳到后面的章节开始阅读。本文不是为了创造新的理论、追求 novelty 等目标而写，只是为了尽自己努力去理解观察到的现象。当然同样的现象也可以用其他的理论来解释，也欢迎大家讨论，找到不同理论之间的联系。

模型训练的无损压缩解释

本章假设读者理解 GPT 的基本原理。出现的对数函数 log 均以 2 为底。

假设 Alice 希望把一个（可能无限长）的数据集 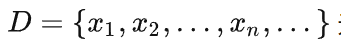无损地传送给 Bob。不失一般性，我们假设

• x_t 表示词表大小m=256的一个 token，即
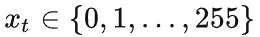
• Alice 和 Bob 都有足够的能源（能用作计算）
• 假设现在已经传输了 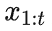， Alice 会将下一个 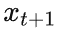编码为 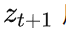后传给 Bob
• Alice 希望最小化传输的数据量 S ，以 number of bits 比特数量来衡量

baseline 传输方法

• 由于 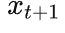的可能性有m=256种，所以 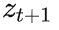可以表示为一个 8 bit 的整数（即一个 byte）。
• e.g.，当 时， 表示 。
• 这时需要传输的位数 。
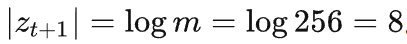• 其实，Alice 还要讲上面的方法写成代码 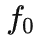，在一开始传输给 Bob。

这样传输一个大小为 n 的数据集 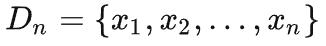的代价 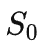为

baseline 方法的概率解释

baseline 方法对于 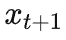的分布没有先验知识，故 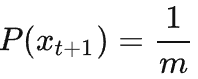是一个离散均匀分布。此时其自信息为

故此时 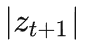也可以看作是 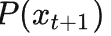的自信息。

基于神经网络训练的无损压缩方法

我们考虑利用一个 Auto-Regressive 神经网络如何进行压缩。具体的，我们考虑这样一个过程：

• 首先，Alice 将一份的 Auto-Regressive 神经网络 m 的训练代码 f 发送给 Bob。该模型输入 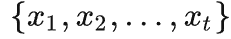， 建模 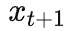的离散概率分布
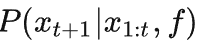
• 实现上可以是一个 Decoder-only Transformer、或者 LSTM/RNN。
  
• 离散概率建模可以用 Softmax 来实现。
• 注意，"模型大小" 这个变量写在了 f 里，但模型的 weights θ 其实是由 f 初始化并持续训练的。可以把模型的 θ_t 看作 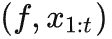的一个函数
• 模型的参数 (weights) θ_t 由 Alice 和 Bob 各自初始化，初始化的方法和随机种子都写在训练代码 f 里，所以初始时刻双方的 θ_0 相同，并且会随着传输进行而同步更新，因此 θ_t 是一个 的函数
• 假设 Alice 已经将 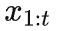传给了 Bob，现在考虑如何将 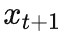编码为 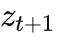传给 Bob。
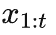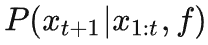• 此时双方按照相同的代码 f 及相同的数据 对网络进行训练，双方都有同样的模型。此时双方对 的概率分布都有相同的建模 。后面若未注明，我们简写为 。

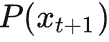• 由于 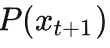是个离散概率分布，其所有可能取值的和为 1，故我们可以将每个可能的取值的概率都表示为一个和概率大小一样的区间。这些区间首尾相接，刚好形成了[0,1]  区间的一个划分。假设 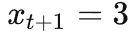为图中箭头所指的取值（不失一般性，这里是预测概率不够高，网络的建模能力还不够准确的情况）。

• 我们考虑按照如下方式将 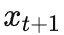编码为 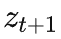：在上图 [0,1] 上对要 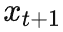所在的区间进行二分查找，从 0.5 开始判断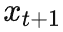， 在右边则判断 0.75，依次类推，直到查找的数字落在 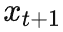所在的区间，并将这个过程的动作下来：

每次查找的动作都会有两种结果：向左或向右。

• 若令 1 表示向右，0 表示向左，那么上面的查找过程便可以表示为一个长度为 3 的动作序列：

• 刚好可以用一个 3 个 bit 的二进制数字 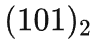来表示

• Alice 将这个动作序列编码为一个 3 个 bit 的二进制数字 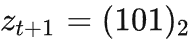，发送给 Bob。

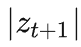• 等价于二分查询的次数。
• 在这个例子里

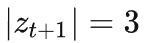
• Bob 收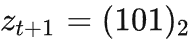到 后，得到 的过程如下

• 首先 Bob 也预测得到分布
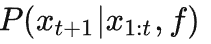
• 然后根据 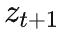代表的动作序列，复现二分查找的过程，得到 0.6875 这个有限精度的实数
• 找到这个实数所在的区间是第 4 个（zero-based）区间，则 Bob 解码

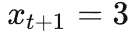
由此我们实现了 Alice 将 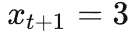根据 Alice 和 Bob 共同知道的概率分布编码为 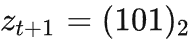传输给 Bob，并且 Bob 根据同样的概率分布将其解码回 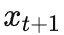的无损压缩传输过程。我们对比 baseline 方法可以发现，本来要传 8-bit，现在只用传 3-bit，传输的数据量有了显著降低。

整个过程每步都很严格，我们将一个参考的实现放在了这里（https://github.com/zxytim/arithmetic-encoding-compression）。这个简单的 proof-of-concept 的实现里，当 codebook size =  2^20时，最高能达到 75% 的压缩率。

实际上，若 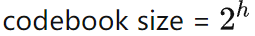，那么极限压缩率大约在

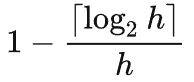
传输代价的计算

既然刚才我们讨论了一个看起来能利用已知概率分布降低传输量的方法，那么我们自然想知道，如何计算所需要的比特数？由于二分查找的可能提前结束，期望意义上的查询次数证明 在这里，也有 比较简单的解释。由于我们希望最小化传输量，那么优化传输量的上界，即 “最多查询次数” 也是殊途同归的。

由此我们计算一下这样二分查找的上界，这里提供一个直观的思路。我们接着用刚才 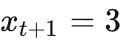的例子：将 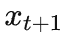的区间均匀铺满整个 [0,1] 的区间，假设 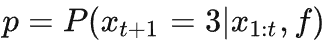，那么会分成 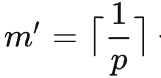个区间，那么大约要查询 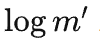次。忽略各种取整误差，可以知道最大二分查询的次数 。

实际上，查询次数的上界为

由此可知传输数据集 D_n  的代价 S_1

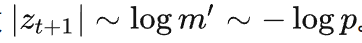进一步观察，我们发现 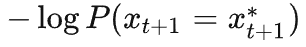其实就是训练时 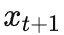这个 token 的 loss。所以我们可以进而发现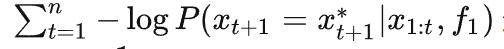， 这一项其实就是训练曲线下方的面积：（实际实现中差个常数 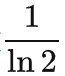，因为 torch.nn.functional.cross_entropy 算的其实是 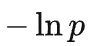，这里为了理解就省去了）

从而压缩率 r_n

假设训练稳定，loss 平滑下降收敛 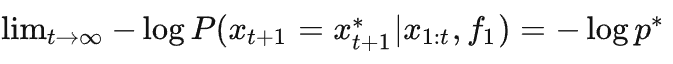，那么当数据集 D 无限长时，压缩率

讨论（从这里开始不 self-contained，有猜测，并且没有 truthfulness 保证）

• 压缩率的极限是

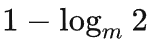
• 当 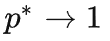时（预测的完全准确），压缩率的曲线如下图

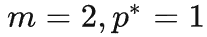• 时压缩率为 0 是为什么？

• 这里我们的方案是考虑一个较大的词表（字符集）。当 m = 2 时二分查至少会用 1 bit，而 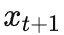本身也只占 1 bit，所以此时二分查找的方法无法提供任何压缩。
• 此时可以考虑使用别的压缩方法，如

• 当 x_t 到 x_(t+k) 的 k 个 bit 都等于 softmax 的 argmax 时，我们可以只传输 k 这个数字，此时只会传输 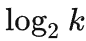个 bit。
• 易知当 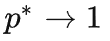时，压缩率
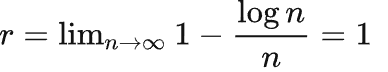
• 这里的目的是讲解压缩和智能的关系，并不是 “如何追求最高的压缩率”

• Auto Regressive 模型的 训练过程 是在 显式的对数据集进行无损压缩

• 如果按照上述方式计算并存储 z_t，那么 "训练代码 + 所有的z_t" 便是对数据集 D 的无损压缩。只是我们平时训练中计算得到下一个 token 的分布，并且计算 loss 进行反传后，便扔掉了这个分布，自然也没有计算并存储z_t 。但是 “无损压缩” 和 “模型训练” 的过程是等价的。
• “Alice 对 Autoregressive Model 的训练过程 + 二分编码” 等价运 zip 软件包的过程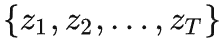， 对应 .zip 文件。解压 .zip 的过程则对应 “Bob 的 Autoregresive Model 训练过程 + 二分解码”
• 所以 “ 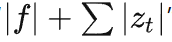” 和 “sizeof (zip 软件包 + .zip 文件) 这两者在概念上是等价的。

• weights 并不是对数据集的压缩表示

• 大部份人会先验地认为 “训练是把数据压缩到了神经网络的 weights 中”。ChatGPT Is a Blurry JPEG of the Web 里虽然提到了无损压缩的 Hutter Prize， 但因为  没有被存下来，而被看做了 lossy compression。
• 进一步，我认为 weights 并没有存下对数据集的压缩。
• 我们从一些例子入手，比如 OpenAI 提到的 Grokking 现象

• 考虑用一个 Transformer 学习同余除法 (Modular Division) "a /b mod 97 = c" 这个问题，其中 a 和 b 的取值为 0～96 的整数。等价于找到一个 c 使得 b * c mod 97 = a mod 97
• 数据上，这个问题一共只有 97^2 ~= 10,000 个数据点，把其中 5,000 当作训练，剩下 5,000 当作测试。
• 训练中的准确率如下图（from Grokking paper)

• 这里有趣的发现是，训练集上很快准确率到达 1，验证集上 "overfitting" 而一直学不会，直到 3 个量级以上的训练步数后，也慢慢会了，准确率趋近于 1。这里说 “overfitting” 是因为，按照传统统计机器学习的观点，随便一个 Transformer 的 VC dimension 都会非常大，在一个只有 5000 个样本的这么简单的训练集上训练几乎就是奔着 overfitting 去的。
• 如果 weights 在训练中随着 training loss 下降 仅仅 在更完美地记忆原始数据集，那么不应该能在 validation set 上能达到 1， 因为真的是一点 validation set 都没见过。
• 如果这个例子会有 “数据量太少” 的 concern，那么可以考虑类似的 “8 位数加法” 的问题，一共有  10^16个样本，基本上不可能学习完。后面的实验表明是能学出来的。如果随便挑两个 8 位数作为 validation，那么也是几乎一定没有在训练集里出现过的。
• 那么 weights 既然不是对数据的压缩，那么到底存了什么呢？

• weights 是对 “智能” 的表示

• 这句话有点民科的感觉 ，但其实想说的是，weights + transformer 计算了数据分布中可解释的部分（后面会展开）。
• 另外一个角度，“智能” 其实是消耗能源用 Transformer + SGD 做压缩后的副产品 (by-product)
• 我们继续考虑 8 位数加法的例子，数据是均匀随机生成的，每字符就是一个 token （没有 bpe），并且沿用 auto regressive 的方式来训练。这其实就是一个常见的 GPT 训练的子集。比如我们考虑下面这个例子用来做训练好的模型的验证
• 17282456+79546852=96829308
• 当训练完全收敛时，对于这个序列的 loss 应该会长下面这样

• 因为前面两个数字的每一位都是从 0~9 均匀随机的，所以其实模型对此无法准确预测，进而只能等概率预测是 0~9 是个数字中的某一个，故
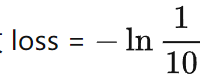
• “+”，“=”，以及最后的答案都是确定性可以预测的，所以 loss = 0
• 聪明的你应该发现了，这其实就对应这个分布的 aleatoric uncertainty 和 epistemic uncertainty。这个例子里：

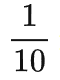• 选择某一个被加数里的数字是不可学习的 aleatoric uncertainty
• "+"、"="、8 位数字的答案、以及从无先验的每个字符 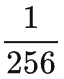的概率变到 0～9 每个字符 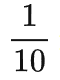的概率的信息差，是可学习的 epistemic uncertainty。而这一部分，就是我们要学习的 “智能”。

• 自然，前文提到的 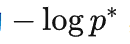其实就是 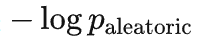，即只剩下了不可解释的随机部分。
• 这里（https://github.com/yulundu/compression）是一个使用 mingpt 的参考实现， 训练的结果 (wandb) 如下：

• Loss 曲线

• Accuracy 曲线

• 实际实现中

• 字符集为 0-9,s,e,+,= 共 14 个字符
• 序列长度为 1（s 开始符）+ 8（数字 a） + 1（+ 号） + 8（数字 b）+ 1（等号）+ 9（答案）+ 1（e 结束符） = 29
• 但因为是 predict 下一个字符，所以训练长度为 28
• training 比 validation 还差且 accuracy 没有到底是因为没注意到 mingpt 里训练 默认带 0.1 的 dropout

• loss 的收敛点大约是 1.31 左右，我们计算 "理论最低" loss

也是可以 match 上观察的。其中

• 16是两个 8 位数字，因为其随机性而没有办法压缩。
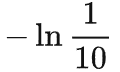• 是每个数字都均匀有 10 种可能。之前提到过，pytorch 实现用了自然对数。
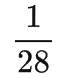• 是序列 loss 算了平均值。

• 对数据进行最高效的压缩，即希望能最准确的预测下一个 token。找到了规律，则能把 epistemic uncertainty 降到 0，而剩余的不可压缩部分，便对应剩下的 aleatoric uncertainty。
• 不过一个令人沮丧的事实是，除非我们能精确描述数据的分布

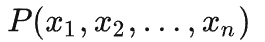
（如 8 位数加法），我们没有办法知道我们是否收敛到了 。

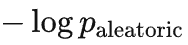• 等一等，你只是在拟合训练集么？为什么能推导出测试集泛化？

• Good question from @汪彧之
• 这里面有个很有趣的角度：是的，没错，训练是在拟合训练集。但在 autoregressive 的场景里，假设数据集里每个 token 都只看过一遍的话，那么 所谓的 "training loss" 其实是 "next token validation loss"。
• 类似的，在传统的过多遍数据集的场景下（如 ImageNet），第一个 epoch 的 loss 是可以看作和压缩率有线性关系的。但从第二个 epoch 开始，我们 empirically 知道模型的能力还在提高，但我暂时无法用压缩的观点来看 loss 的下降了。
• 思考题：对数据训练两个及其以上 epoch 时该如何用压缩观点来解释？跳出来看，这个问题的意义有多大？

• 压缩有限样本可以学习到真的 “智能”

• 考虑在 有限 但 足够多 的数据的情况下，压缩是 有可能 学习到真的智能的。
• 在有限在足够多的样本的情况下，如果假设我们的压缩算法（a.k.a, for now, Transformer + SGD) 对于当前的数据做训练时 training (a.k.a, next token validation) loss 能 “比较稳定” 的下降，并且 从某个 step T 开始，training error 都是 0（更精确一点是 epistemic uncertainty =0），能对未来 token 的预测完全准确则该模型就真的 “懂” 了数据的生成规律。

• 思考题：这里面缺少很多严格的数学定义，该如何严格地 formualte 这个命题？

• 所以我们知道， 有限样本训练也是可以达到最大压缩率的

• for skeptics: 是的，收敛率的问题没有讨论，可能 “有限” 也大得离谱，但我希望收敛速度尽可能快，也希望有更多人来研究这个事情。

• 涌现 （emergence） 可以理解为在 loss 下降过程中，数据的某个子集的 epistemic uncertainty 突然快速下降，模型突然开始 “悟” 了。

• 由于 training dynamics 的复杂性，据我所知还没有办法预测什么时候能力会涌现、在什么时候涌现。我猜测涌现可能只是（我们目前还搞不太懂的） training dynamics 的一种行为；“慢慢学会” 其实到最后也没有太大问题。
• @Xiangyu Zhang 有个更符合中文语境的说法叫做 “顿悟” 。

• 涌现得 到的人可以理解的智能，是和人没有区别的智能

• 在训练过程中压缩率越高，模型越 ” 智能 “

• 我们知道在训练过程中的 loss 其实是 validation loss，且当 loss 下降时，我们对于 next token 的传输压缩率会越高，再考虑到有限样本也是可以达到最高压缩率的，所以模型也就会越来越智能。

• （empirically）模型越大压缩率越高，从而模型越智能

• 我们已经知道了，模型训练过程实际上是在对数据集做无损压缩。经验上，我们知道模型越大，模型能力越强。我的理解是，“大模型好” 这个说法实际上是在第三层：