这道题的来源是一道比较经典的
动态规划
题目,名为
二维费用背包问题
。原本的问题为
“设有n件物品,每件物品想要放入背包有两种不同的费用,同时每件物品有着不同的价值。两种费用加和可付出的最大值(也即背包的两种容量)给定。求解将哪些物品装入背包可使价值总和最大。”
我们将现在的题目转换一下,将给定的字符串看作要放入背包的物品,每件物品的两种不同花费认为是每个字符串0和1的个数,而m和n可以看作背包的两个容量。这样一来我们可以将题目解释为
“我们要从给定的字符串中挑选字符串
每挑中一个字符串要花费两种不同的费用(0和1的个数)
两种费用的和分别不能超过m和n
求最多能挑选多少个字符串。”
这样解释后就可以看出这道题和原题的相同之处了,两道题的唯一区别点在于原题的每件物品价值不定,而对于我们这道题,每个字符串的
价值
都是相同的并且均为1。
这个状态转移方程基本来源于二维费用背包问题的解法。我们先给出状态转移方程再进行解释。状态方程为:
其中,F[i, v, u]表示在背包容量(0和1的最大个数)分别为v 和u 时,前i个字符串可产生的最大价值(被挑中的最大字符串数)。Ci和Di用来表示第i个字符串0和1的个数。对于第i个字符串来说,它只会有两种状态,
被挑中
和
不被挑中
。
❖❖若第i个字符串被挑中,问题就转化为“前i个字符串放入容量为v - Ci, u - Di的背包中的最大价值”,则价值为F[i, v – Ci, u - Di] + 1。
❖❖若第i个字符串未被挑中,则问题就转化为“前i - 1 个字符串放入容量为v, u的背包中的最大价值”,价值为F[i - 1, v, u]。
既然对于第i个字符串只有这两个状态那么我们取两者
价值最大
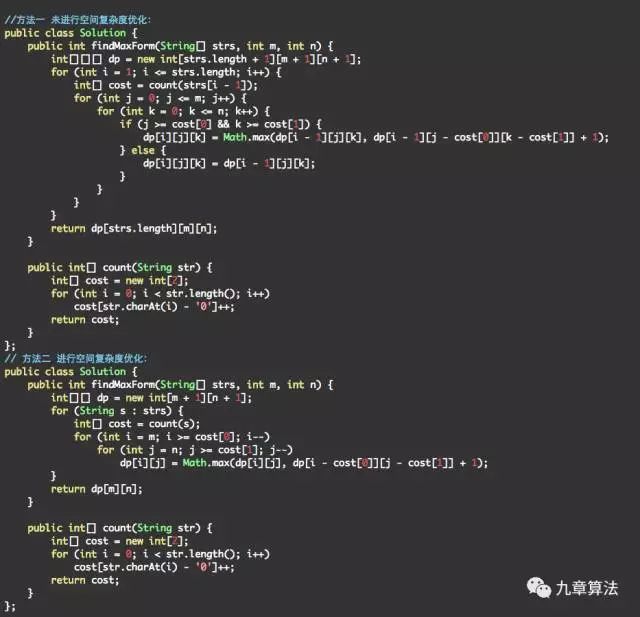
的那一个即可。其实到这里已经可以了,但是这个解法的空间复杂度有一些高,我们可以思考优化。
我们可以发现在状态转移时,前i个字符串的状态总是依赖于前i-1个,而不依赖于之前的状态。也就是说历史状态(前1到前i-2个字符串的状态)其实是没有作用的,那我们思考可不可以将其优化掉。事实证明是可以的,我们状态方程随即变成这种形式:
但是要注意如果采用这个状态转移方程,对于v和u来说,这两层循环必须使用
倒序
,不然就会破坏前一层的值,从而无法计算出正解。
这一种优化在理解上其实还是稍有难度的,因为我们现在只记录一层的状态(原先的解法记录了L层状态,L为给定字符串的数量),所以保证前一层循环产生的状态值不会被新一层的循环破坏掉是关键。参考程序中给出优化前后的两种不同解法供大家理解思考。
这道题的关键是将看似不常见的题目转化为常见模型,这是对面试者算法熟练度和思维的一个考验。能快速发现题目的动态规划本质并给出正解可拿到hire,若还能对空间复杂度做出优化可拿到strong hire。
http://www.lintcode.com/zh-cn/problem/backpack/
春招帷幕已经拉开,
如何短时间全面、系统复习面试必备的知识?
九章算法全套IT求职课程帮你少走弯路!
《九章算法班》
《系统设计班》
《Big Data 项目实战班》
《Android 项目实战班》
《算法强化班》
硅谷顶尖IT企业工程师直播授课
正在报名中!
报名登陆官网www.jiuzhang.com
或点击文末“阅读原文”