网上讲高斯过程回归的文章很少,且往往从高斯过程讲起,
我比较不以为然:高斯过程回归(GPR), 终究是个离散的事情,用连续的高斯过程( GP) 来阐述,简直是杀鸡用牛刀。
所以我们这次直接从离散的问题搞起,然后把高斯过程逆推出来。
这篇博客有两个彩蛋,一个是揭示了高斯过程回归和Ridge回归的联系,另一个是介绍了贝叶斯优化具体是怎么搞的。
后者其实值得单独写一篇博客,我在这里做一个简单介绍。
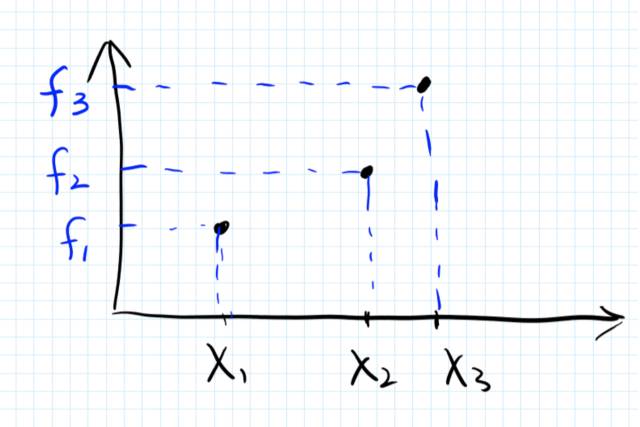
假设有一个未知的函数f : R–> R
在训练集中,我们有3个点 x_1, x_2, x_3, 以及这3个点对应的结果,f1,f2,f3. (如图) 这三个返回值可以有噪声,也可以没有。我们先假设没有。
so far so good. 没什么惊讶的事情。
高斯过程回归的关键假设是:
给定一些 X的值,我们对Y建模,并假设对应的这些Y值服从联合正态分布!
(更正式的定义后面会说到)
换言之,对于上面的例子,我们的假设是:
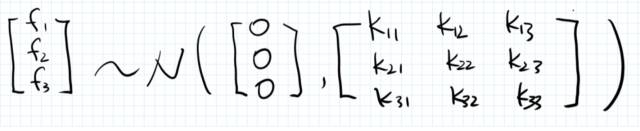
一般来说,这个联合正态分布的均值向量不用操心,假设成0就蛮好。(讲到后面你就知道为什么了)
所以关键是,这个模型的协方差矩阵K 从哪儿来。
为了解答这个问题,我们进行了另一个重要假设:
如果两个x 比较相似(eg, 离得比较近),那么对应的y值的相关性也就较高。换言之,协方差矩阵是 X 的函数。(而不是y的函数)
具体而言,对于上面的例子,由于x3和x2离得比较近,所以我们假设 f3和f2 的correlation 要比 f3和f1的correlation 高。
话句话说,我们可以假设协方差矩阵的每个元素为对应的两个x值的一个相似性度量:
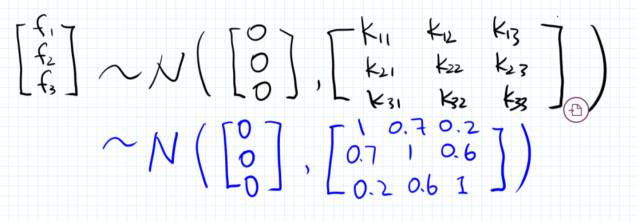
那么问题来了,这个相似性怎么算?如何保证这个相似性度量所产生的矩阵是一个合法的协方差矩阵?
好,现在不要往下看了,你自己想3分钟。你也能想出来的。 提示:合法的协方差矩阵就是 (symmetric) Positive Semi-definite Matrix (。。。。。。。。。。。。思考中) 好了时间到。
答案: Kernel functions !
转自: 机器学习算法与自然语言处理
点击“阅读原文”查看全文





