
图形作为一种几何语言,是信息的重要载体,在解几何题时,如果只是一昧地教给学生就题论题,学生就不会把图形看“活”,至于图形中更为有用的信息就得不到挖掘,更谈不上得到其中深刻的规律了;反之,如果注意图形的引申、变化,那么往往可以得到一些令人满意的结论,这对训练学生的思维大有裨益,事实上,教材中的一些例题、习题往往都隐藏着一些潜在的功能,教师要善于引导学生挖掘问题的各个方面,充分度挥它的功能和作用.
1. 挖掘几何图形的变式功能,培靠学生探究实践的能力
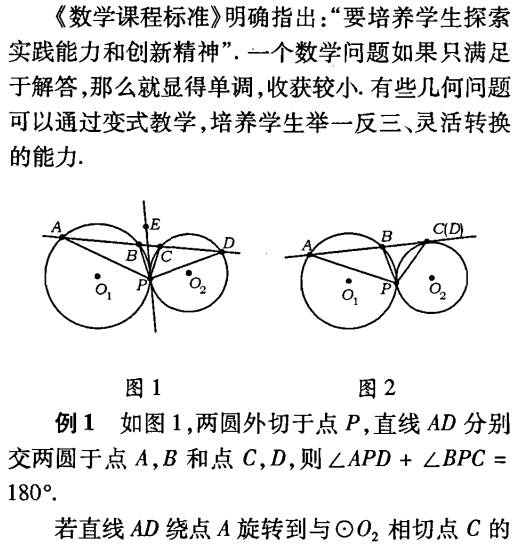
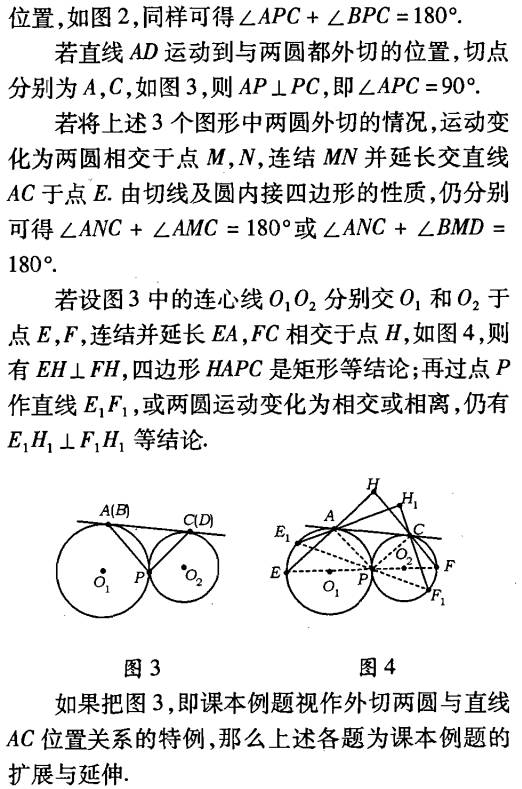
在上述讨论中可以发现:图形变了,但图形的性质及证明的思路不变,即"变中有不变”,用这种运动变化的方法研究几何圆形的性质,不但能收到事半功倍、触类旁通的效果,而且还有利于培养学生的分析归纳和综合概括的能力
2. 发挥基本图形的运用功能,让学生掌握解题的玥匙
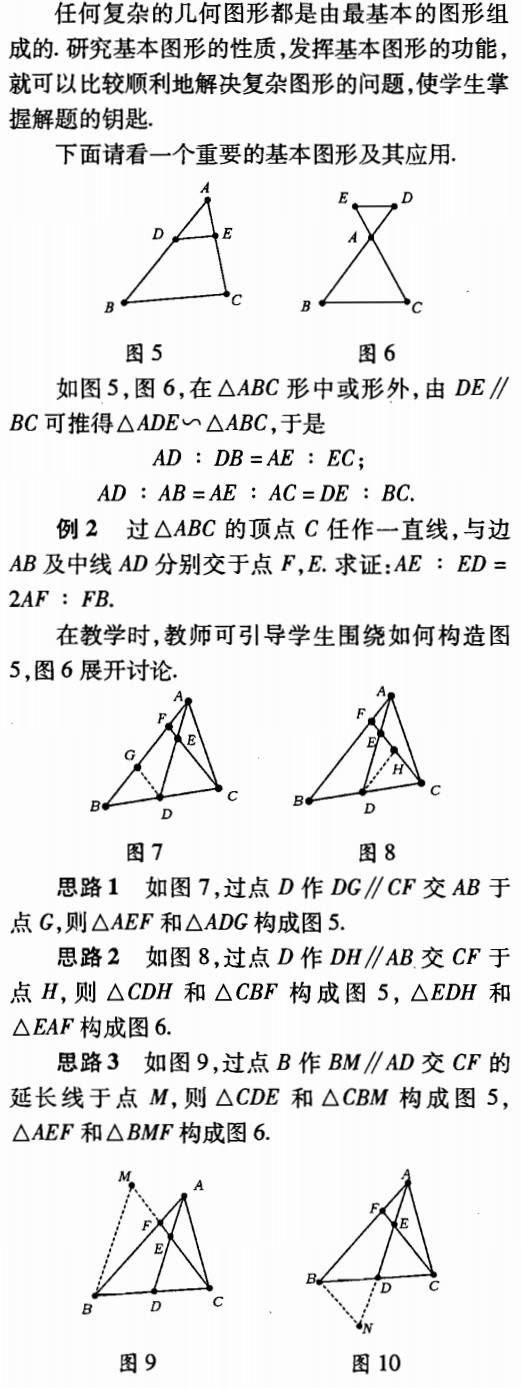

3. 研究习题结论的延伸功能,培养学生的创新性思维

对课本中的例题、习题进行深入挖掘与引申, 加工成多个结论,便会得到一系列纵横沟通的好题目,这不仅有助于克服题海战术,还能激起学生探索问题的欲望,拓宽他们的思路,活跃思维,发展创新能力
如有帮助,欢迎分享转发
【往期内容】
以定制动,一类动直线问题的探究
天下初三一般黑,岂有不累
原来数学史就是一部八卦史
梁启超10句话,9个子女皆成才
上海高考数学知识点考查难易度分析
你这样,这辈子别想学好数学
如果孩子成绩不好,读读这篇文章
解题之道,无他,手熟尔
做错题,真正原因不是粗心
这9种学生永远拿不到高分





