转载自:公众号 王的机器
供稿人:王圣元

金郡 (King County, Washington) 是美国华盛顿州的一个郡,郡治西雅图。斯蒂文是华盛顿大学 2016 应届毕业生,毕业去了一个房地产公司做数据挖掘。老板第一天就丢给斯蒂文一张 csv 表,里面有 21000 多个房屋数据,包括其价格,平方英尺,卧室数,楼层,日期,翻新年份等等 21 列数据。下图是该 csv 的缩影:
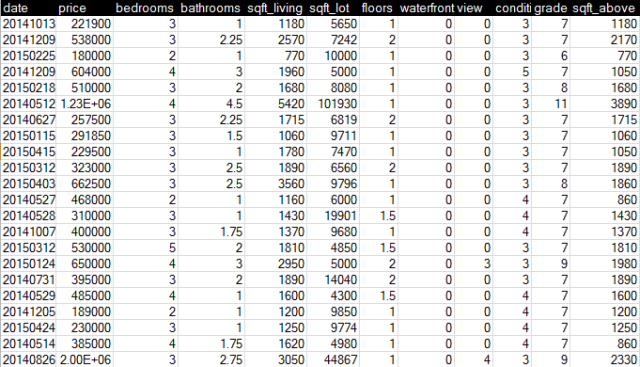
斯蒂文:你想要我怎么做?
老板:我想看你能做出点什么?
斯蒂文:Yeah?
老板:Yeah!
经过一周的努力,斯蒂文用以下方法一步步探索了金郡的房屋数据 (本帖主讲)
-
线性回归
-
多项式回归
-
岭回归 (正规化)
-
套索回归 (特征选择)
以上四条教程可参见:
http://dwz.cn/5Oweak
上面所有的模型比如岭回归和套索回归都是直接用 scikit-learn 包里面的,此外斯蒂文也自己编写了岭回归的梯度下降法 (gradient descent) 和套索回归的坐标下降法 (coordinate descent),同时也研究了下岭回归和套索回归如何防止多项式回归的过拟合问题 (本帖不讲但会给其 notebook)
-
多项式 vs 岭 vs 套索
-
岭回归 (梯度下降)
-
套索回归 (坐标下降)
所用的 ipython notebook 和 csv 文件如下图:
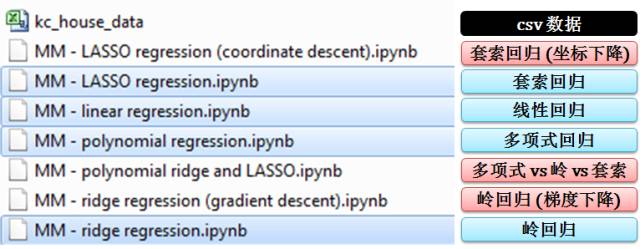
进入平均机器公众号,在对话框回复 ML5 可下载代码 (ipython notebook 和 html 格式) 和数据 (csv格式)
下面斯蒂文用 ipython notebook 带你们玩转金郡。
0. 前戏
如果你的计算机上没有 Python,可以使用 Anaconda Python 发行版来安装你需要的大部分 Python 包。主页网址 https://www.continuum.io/downloads,网页如下图所示:

当你下载安装完 anaconda 后,在命令框里输入 "ipython notebook"
系统会自动跳到一个类似于一个管理文件的网页,如下图所示的就是本帖要讲解的所有 notebook:
点开每一个 notebook,斯蒂文每次做的前三个步骤都是一样的:
-
设定正确的路径
-
引用要调用的包
-
用表格和图研究数据
第一步:设定正确的路径

第二步:引用要调用的包
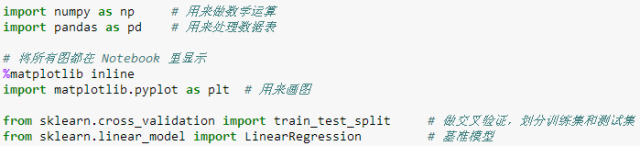
上图是以线性回归需要的包为例,而本贴讲的需要使用了几个包是:
"import A as B" 这个格式是说引进 A 包用假名 B 来代替,为什么用假名呢?你看看上图里假名 B 是不是比实名 A 要简单。当你要想用 A 包里面的函数 f,你可以写成 A.f 或 B.f,但显然写成 B.f 使得代码便于读写!Python 程序员喜欢用 np 和 pd 来代替 numpy 和 pandas,当然你有自由定你的 B。假名 B 除了可以代替一个包,还可以代替一个包里的函数,比如 plt 通常代替 matplotlib 包里的 pyplot 函数。
第三步:用表格和图研究数据
用 pandas 里面的 read_csv 函数来读取数据并存储到数据表 sales 里面,再用 head() 和 tail() 函数看前五行和后五行的数据,注意下图最左边有个 5 rows × 21 columns 的字样,表示你看到的表有 5 行 21 列。
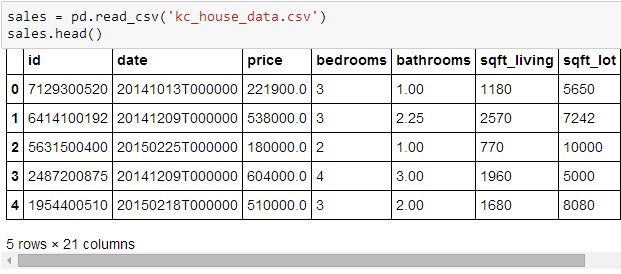
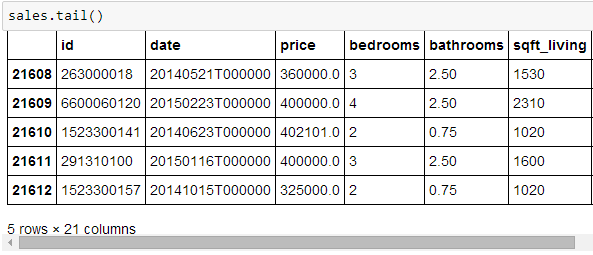
注:上截图里没有把整个数据表信息截屏全,但是在 notebook 里,可以拉动下面滚动条自由查看数据
对于数字类型的列,可用 describe() 函数的产出其数据的个数 (count),均值 (mean),标准差 (std),最小值 (min),25, 50 和 75 百分位数 (25%, 50%, 75%) 和最大值 (max)。50 百分位数也就是中位数 (median)。看 count 那行可以一下看出是否有数据缺失,在本例中每列对应的都是 21,613,因此数据是全的。
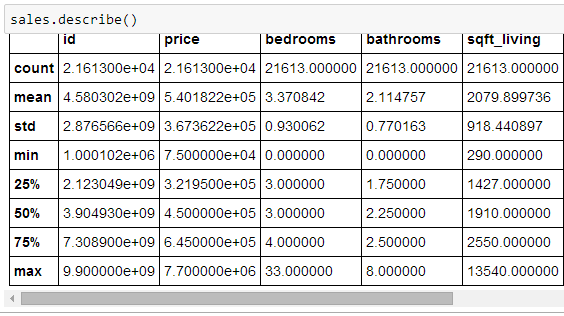
此外用 shape 函数得到数据表的大小,(21613, 21) 代表着 sales 有 21613 行 21 列。而用 dtypes 函数得到每一列的数据类型是什么。注意到 sqft_living 对应的类型是 int64,它代表着长整型数据,范围是 [-263, 263),即 -9223372036854775808 ~ 9223372036854775807之间。这个细节平常我们都不会注意的,但这次此细节对多项式回归非常重要,等到第三章再提。(当你亲自用程序解决实际问题时,你会遇到平时想都没有想过的问题,当你找出并解决它们时,你的进步会非常快)

图永远比表格更直观,但图最多只能画出三维。根据房屋数据,最合理的建模应该是在价格和面积上。因此我们在建模前想看看它们之间的关系。plot 函数能帮你。从下图可见绝大部分数据聚集在起居室面积 8,000 和价格 400,000 以下。
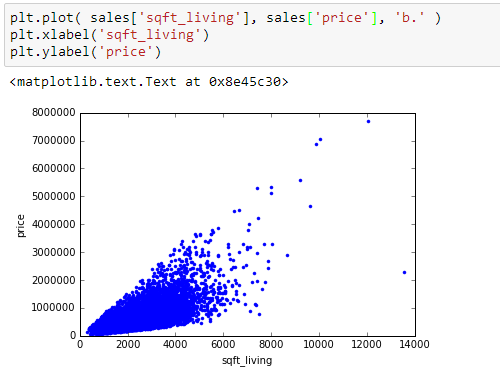
上面几个查看数据的步骤可能不完整或者不是必需的。怎么查看数据的做法没有对错,它的唯一作用就是帮你对数据有个大概了解,幸运的话还可以从表格和图里找到数据的一些不合理的地方,在建模前把它们处理掉,千万不要让“垃圾进垃圾出”这种情况发生。
前戏做完,开始玩转!
1. 线性回归
斯蒂文还是个新手 (noob),他玩的最溜的还是最简单的线性回归。斯蒂文信奉机器学习大拿吴恩达 (Andrew Ng) 说过的话“每次开始建模时要从最简单的模型开始,找到不足慢慢改进” 。对于回归问题最简单的就是单变量线性回归,而斯蒂文老板想要知道的也就是什么变量和房屋价格有关,如何有关,什么样的模型最好?
从最简单模型开始,通常房屋面积和价格正相关 (上张最后一张图可看出此趋势),下面就用数据表 sales 里的含面积和价格列来建模吧。

从上图关于数据表 sales 的列标记看出, 'price' 对应的那栏就是“价格”。但是有很多栏都提到面积,比如 'sqft_living', 'sqft_lot', 'sqft_above', 'sqft_basement', 'sqft_living15' 和 ‘sqft_lot15’,到底要选哪个呢?
-
sqft_living: 起居室面积
-
sqft_lot: 占地面积 (包括前院和后院)
-
sqft_above: 起居室除去地下室面积
-
sqft_basement: 地下室面积
sqft_living15 和 sqft_lot15 不清楚是什么,看数据发现和 sqft_living 和 sqft_lot 基本一样,因此不再管它俩。如果只能选一个面积当自变量,斯蒂文觉得起居室面积对价格的影响最为重要,而这个也是仁者见仁智者见智了。选好 price 做变量和 sqft_living 做自变量,接下来线性回归的操作非常简单:
-
按 80% 和 20% 划分训练集和测试集
-
用 sklearn 里面的 LinearRegression() 模型拟合参数
-
计算测试误差
i. 划分训练集测试集
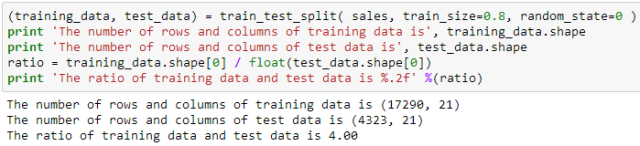
从 sklearn.cross_validation 小包里使用 train_test_split 函数,对 sales 进行划分,其中训练集大小 (train_size) 设为 0.8,而随机状态 (random_state) 设为 0 是为了在机器学习中每次出的结果一样,事实上你也可以设为其它整数。从打印出的结果可看出训练集和测试集的个数比例为 4。
接着将训练集和测试集对应的“起居室面积”和“价格”向量取出,代码如下图:

ii. 用 sklearn 自带模型

代码步骤解释如下:
-
调用 LinearRegression() 模型,将里面一个参数 normalize 设为 True。它的意思就是将特征值标准化,这样可以使得梯度下降计算起来更快收敛。
-
用 fit() 函数在训练集拟合参数。
这是 model 你可以把它看成是个物体 (object),里面有属性 (attributes) 比如参数系数和函数方法 (methods) 比如预测函数和得分函数。整个流程就跟 C++ 或 Java 里面封装 (encapsulation) 的概念一样的。
iii. 计算测试误差
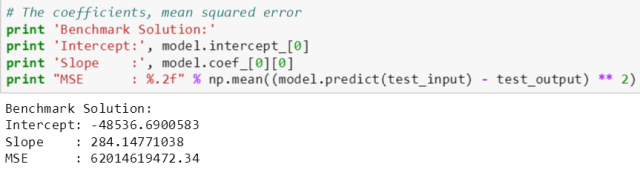
代码解释如下:
-
前两行打印出 model 的截距 (intercept_) 属性和系数 (coef_) 属性的值,截距是个 1 维矩阵而系数是个 2 维矩阵 (为了存储多变量线性回归的系数),因此用 [0] 和 [0][0] 来分别取出截距和系数的值。
-
最后一行打印测试误差就调用了 model 的 predict() 函数,而生成的预测值和真实值的差的平方的均值就是测试误差。
最后画出测试集上的散点图 (蓝点) 和拟合的直线图 (绿线),发现在测试集上的拟合效果一般,尤其对一些面积很大的房子预测出的价格偏低,理想的绿线应该在面积8000至10000之间更向上陡一些。
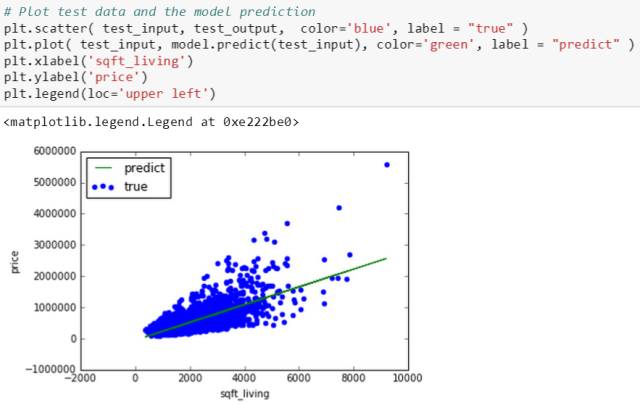
基于拟合效果不好,斯蒂文提高一下模型的复杂度,用多变量线性模型,有两种形式:
没做之前斯蒂文也不知道哪种比较好,只能边做边比。下文第二、三章都是讲形式一,第四章讲形式二。
注:在 MM - linear regression 的 notebook 中,斯蒂文也用了解析解和梯度下降数值解来解以上问题,结果和 sklearn 里的模型产出一模一样。有兴趣的同学可以查阅该 notebook。
2. 多项式回归
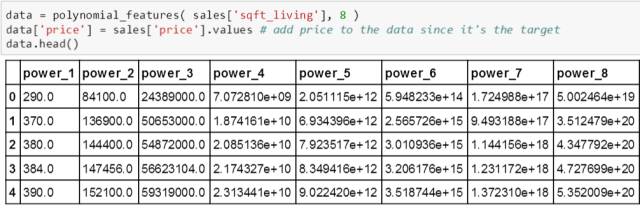
和线性回归 notebook 里的操作一样,斯蒂文首先 a) 设定正确的路径 b) 引用要调用的包 c) 用表格和图研究数据。其中不同的是要对 sales 数据表根据 sqft_living 和 price 大小排序,其原因是为了后面要画出拟合出来的多项式,不排序的话画出的图像锯齿一样乱,因为多项式的曲线图是把拟合出来的每点一个个连接起来。排序函数见下图:
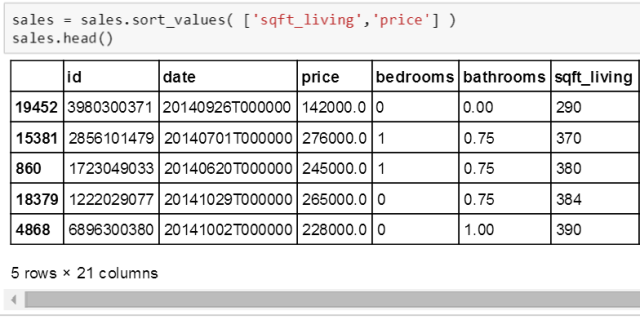
用 sort_values() 函数,里面参数 ['sqft_living','price'] 表示首先按 sqft_living 大小排序,一旦有相同值,再按 price 大小排序,排序默认方式是升序。可以看到 sqft_living 列下的数值 290, 370, 380, 384 和 390。
用多项式做回归前需要一个生成多项式的函数,它的作用就是给定一列向量 X 和多项式次数 n,生成 X 的 1 到 n 次方的一个矩阵。代码如下:
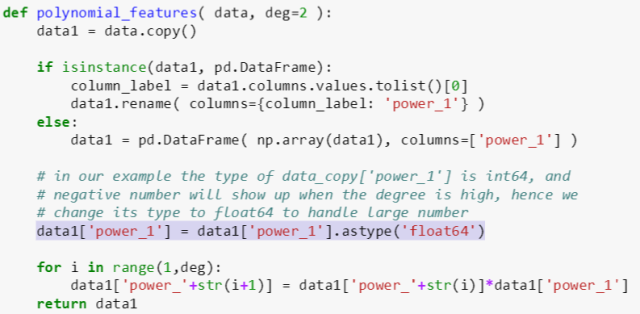
代码解释如下:
-
参数 data 是一个一维向量,可以是数据表 (带标记) 也可以是数值 array。参数 deg 是多项式的次数,默认值为 2。
-
data1 = data.copy() 这行代码表示将 data 里面的值拷贝到 data1,之后在 data1上做任何事情不会影响到 data。
-
if 和 else 是处理数据表或数值 array 的情况。
-
高亮这部分非常重要,astype('float64') 函数将原来 int64 的数据类型转换成 float64,目的是为了能存储更大的数。具体原因见下。
-
最后 for 循环就是生成多项式 1 到 n 次方的值。
接下来我们来看看如果没有执行步骤 d 的结果:
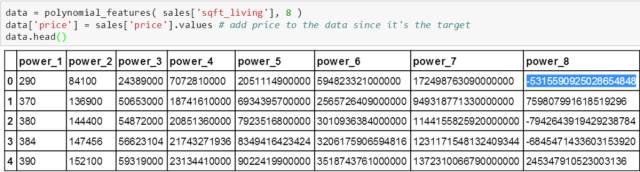
高亮部分是个负值,为 -5315590925028654848 (用 a 表示),而真正的值 (290 的 8 次方) 应该是 50024641296100000000 (用 b 表示)。为什么会是负值呢?原因是当你没把 int64 转成 float64 时,int64 数的范围是 [-263, 263),即上界 9223372036854775807 (用 c 表示)。我们发现 b 比 c 还大,在计算机里 b 要不停的减上界 c 直到 b 小于 0,最后发现 b - 6c 得到 a。
当多项式出现负数项是绝对不合理的,斯蒂文一开始没注意 int64 的范围,觉得够大可以处理绝大部分数值,后来发现模型拟合效果很差,才一步步倒退过来发现 int64 上界比高次多项式值还小的问题,后来讲 int64 改成 float64 (是个非常大的数!!!),发现结果一切合理。如下图所示:
测试下 polynomial_features() 函数功能:
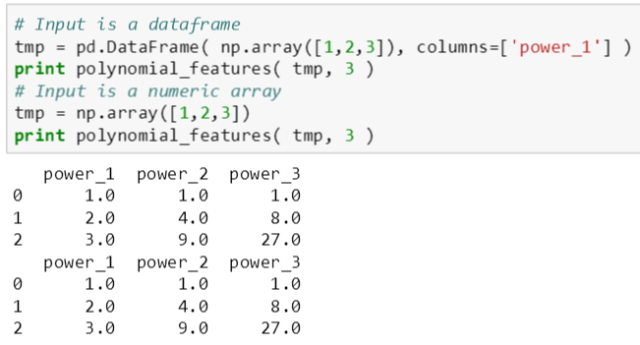
上图验证了此函数在第一个参数是数据表或数值 array 时都能生成正确结果。
接下来斯蒂文自己编写了几个基本函数用来建模、打印多项式系数和画图:


代码解释如下:
-
polynomial_regression() 函数是调用 sklearn 里面的 LinearRegression() 模型,再调用 fit() 函数构建一个 model 的物体 (代表一个多项式的物体)。注意在LinearRegression() 里面 normalize 参数设置为 True,原因就是之后测试的 15 次多项式可能数据比例相差太大 (290 和 290的15次方相差十万八千里)。
-
plot_predictions() 函数画出真实散点和拟合多项式。
-
print_coefficients() 函数打印出拟合多项式的数学表达形式。
-
polynomial_output() 函数一次性使用上述三个函数,使得以后调用起来简便。
到此本章需要编写的核心程序全部完成,下面就是如何用这些程序来研究多项式回归的一些性质了。接下来我们从三个方面来研究:
-
用相同数据,不同多项式次数
-
用不同数据,相同多项式次数
-
找到最佳多项式次数
I. 用相同数据,不同多项式次数
首先用 1 次多项式
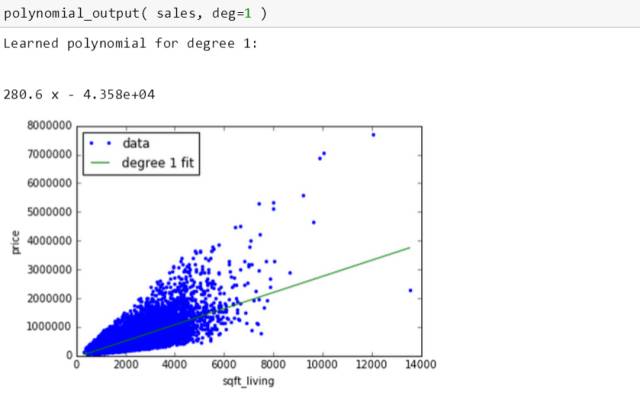
拟合出来的多项式对应的绿线是条直线。
再用 2 次多项式
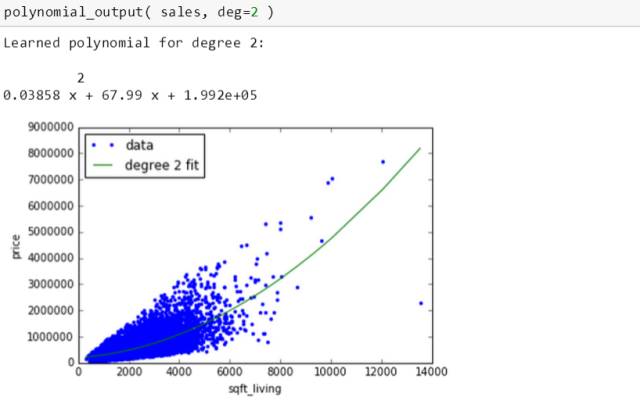
拟合出来的多项式对应的绿线是个抛物条。
再用 3 次多项式
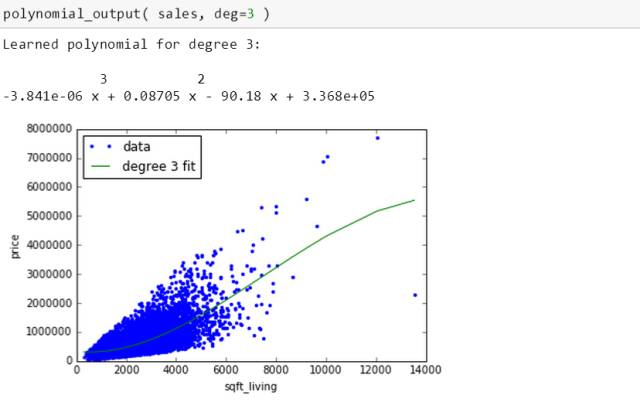
拟合出来的多项式对应的绿线很像抛物线但在边界又有所不同。
最后用 15 次多项式
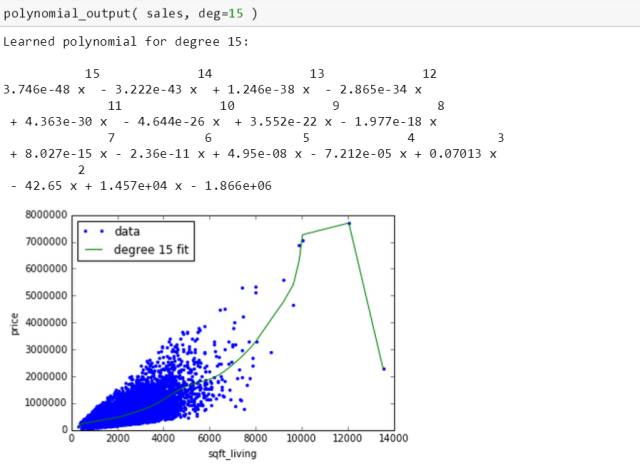
这绿线太疯狂,这系数太狂浪,明显这拟合是失败的。斯蒂文想如果换一套数据还能得到类似的系数和图吗?如果不行,说明 15 次多项式模型过拟合了数据。
II. 用不同数据,相同多项式次数
为了弄清楚15 次多项式模型是否过拟合了数据,斯蒂文将数据 sales 平均分成四份当作训练数据,操作如下:
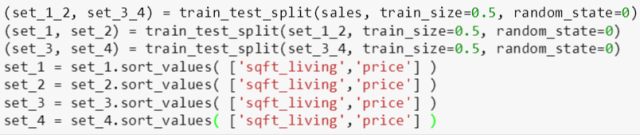
首先将 sales 一分为二,得到 set_1_2 和 set_3_4,再将它们分别一分为二得到四个集 set_1, set_2, set_3 和 set_4。像之前对 sales 数据排序一样,这四个集的数据也要排序 (为了以下多项式画图)。
四个数据集生成15 次多项式的表达式和图为
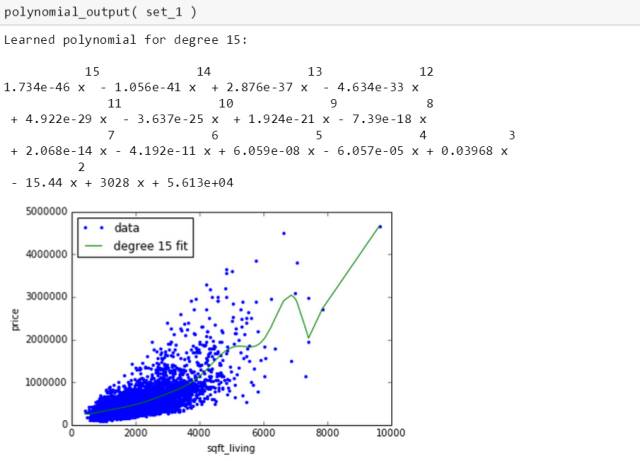
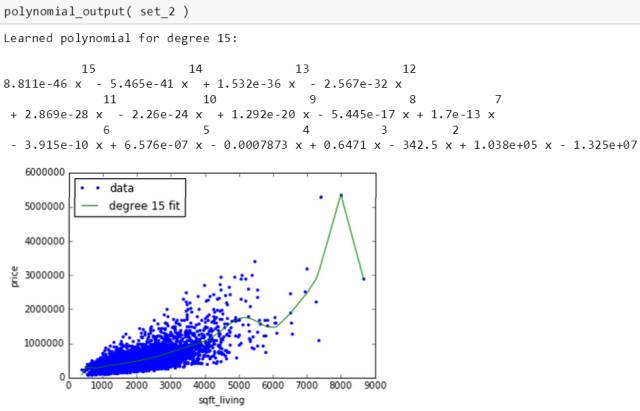
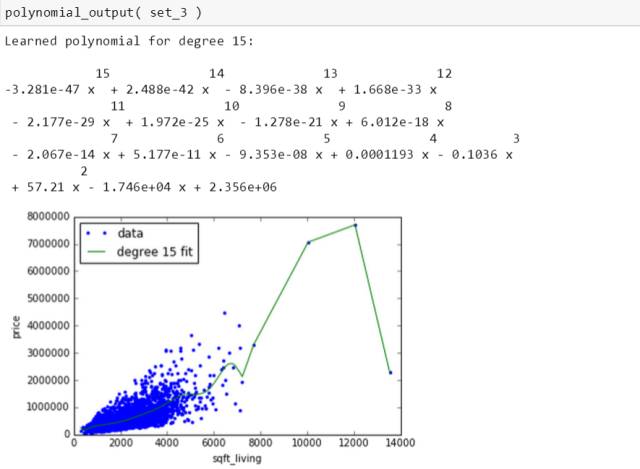
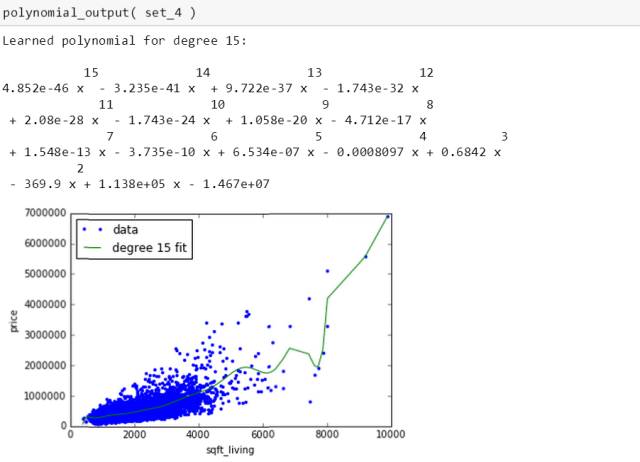
四条绿线千奇百怪,四个多项式也迥然不同,别玩了,这就是过拟合。斯蒂文在第三章会用岭回归来处理它的。
III. 最佳多项式次数
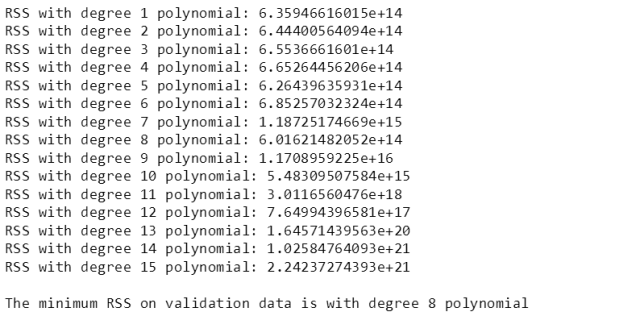
多项式次数有无限多,上小节已经确认15次多项式已经过拟合数据了,次数再往上一定是过拟合,因此斯蒂文只关注从1次到15次,第一步操作就是按 45%, 45% 和 10% 比例来划分测试集、验证集和测试集 (数据总共有 21613 个,数量足够了,因此不用到交叉验证集)。

对于每次多项式,用训练数据拟合参数在计算验证误差,找到最小验证误差对应的多项式次数,本例是 8。因此 8 次多项式是最佳多项式模型!
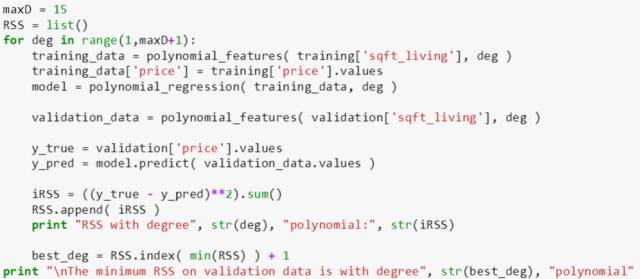
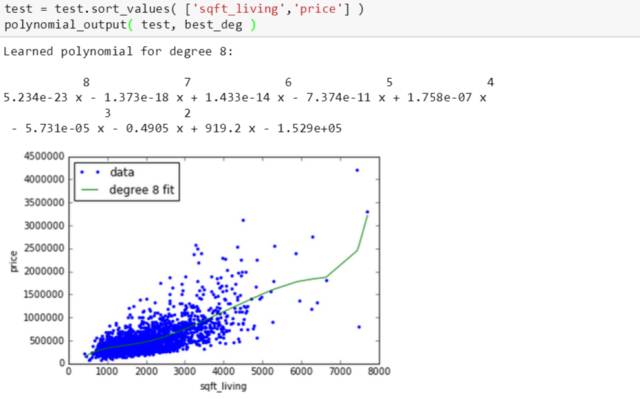
用训练好的 8 次多项式模型来计算测试误差,评估一下模型。

结果看起来还行,绿线起码不会那么张扬跋扈,但是还是有些过拟合。这个是高次多项式的硬伤,唯一灵药就是正规化。斯蒂文准备开始用岭回归了。
3. 岭回归
岭回归需要引进新的包和函数,比如 Ridge 模型和 shuffle 函数。

顾名思义 Ridge 模型是用来做岭回归的 (类比于上章 LinearRegression 模型用来做多项式回归) ,而 shuffle 函数是要打乱数据生成交叉验证集的。
接下来斯蒂文自己编写了几个基本函数用来建模、打印多项式系数和画图:
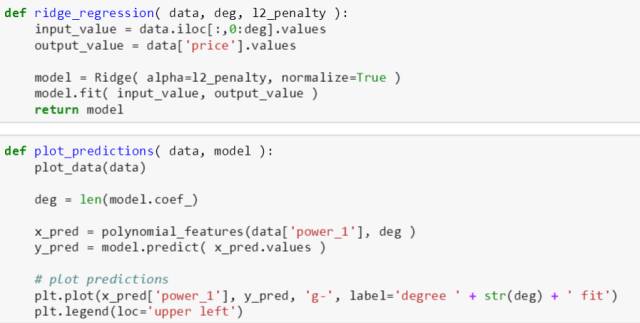
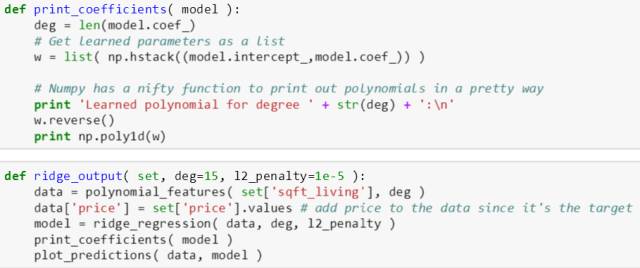
代码解释如下:
-
ridge_regression() 函数是调用 sklearn 里面的 Ridge() 模型,再调用 fit() 函数构建一个 model 的物体 (代表一个正规化的多项式的物体)。注意在 Ridge() 里面第一个 alpha 就是调合参数,第二个 normalize 参数设置为 True,道理和上章多项式讲的一样。
-
plot_predictions() 函数画出真实散点和拟合多项式,和上章一样。
-
print_coefficients() 函数打印出拟合多项式的数学表达形式,和上章一样。
-
ridge_output() 函数一次性使用上述三个函数,使得以后调用起来简便。
到此本章需要编写的核心程序全部完成,下面就是如何用这些程序来研究岭回归的一些性质了。接下来我们从三个方面来研究:
-
用不同数据,小调合参数
-
用不同数据,大调合参数
-
找到最佳调合参数
I. 用不同数据,小调合参数
首先用一个很小的调合参数 10-5,其实基本上没有对参数有任何惩罚,因此画出的图应该和上章多项式拟合画出来的图差不多

由下图可知,小调合参数不能解决多项式回归的过拟合问题
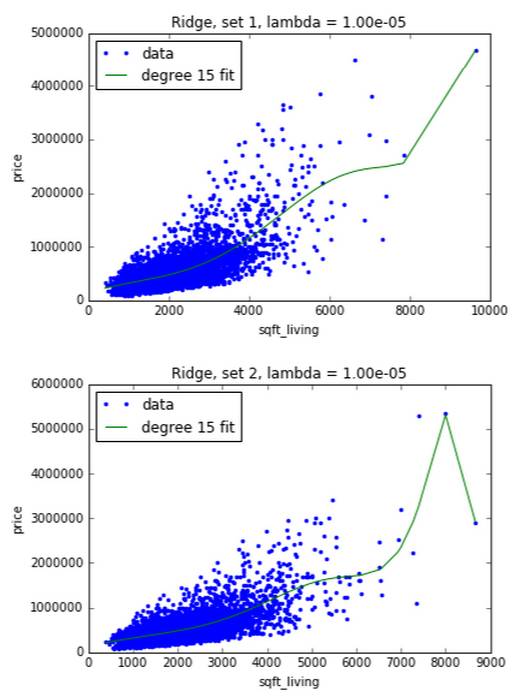
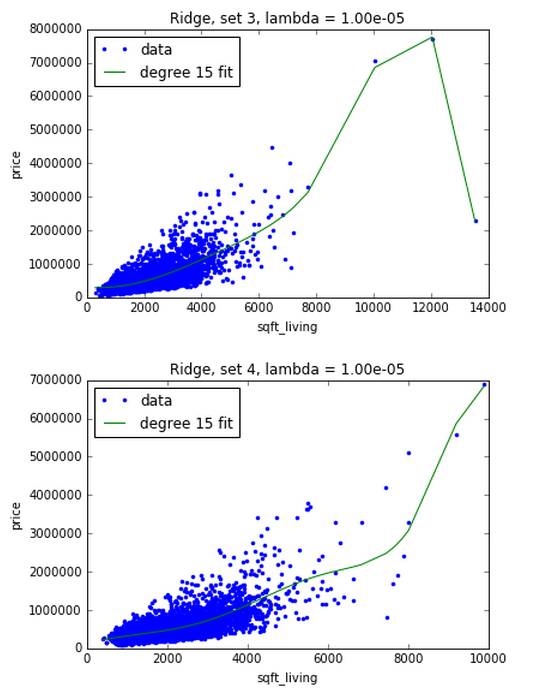
II. 用不同数据,大调合参数

然后用一个大的调合参数 10,由下图可知,每个数据集生成的绿线长的差不多,过拟合问题得到了解决。
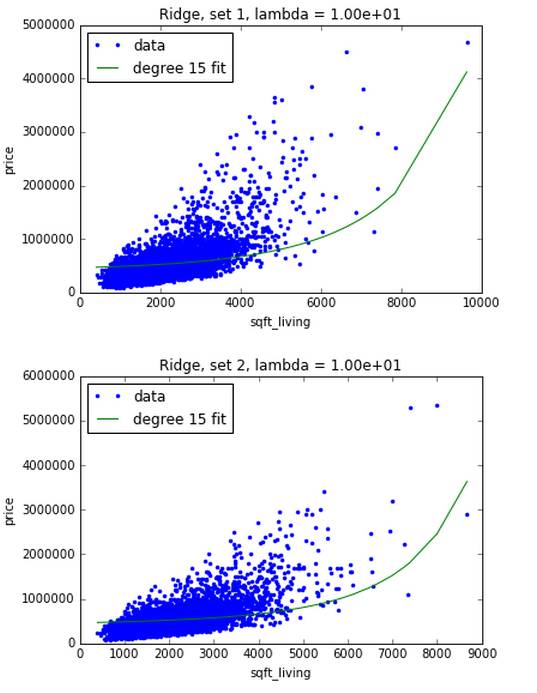
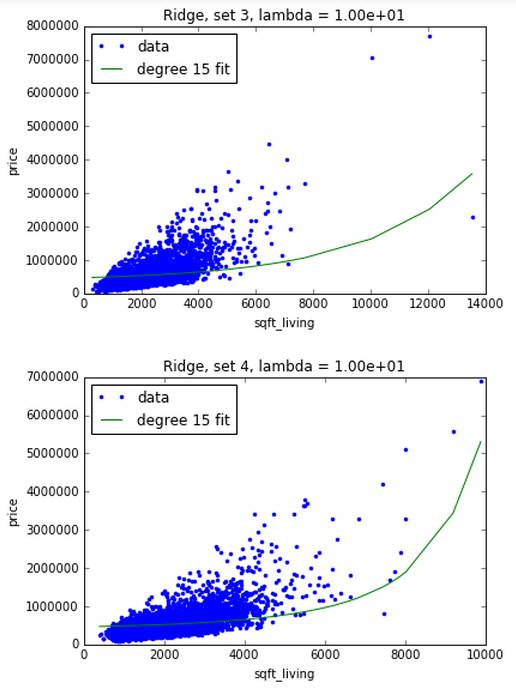
III. 最佳调合参数
调和参数有无限多,这次斯蒂文准备用 10 折交叉验证方法来决定一个最佳调和参数。

首先用 90% 和 10% 来划分训练验证集和测试集,之后用 shuffle 函数将训练验证集内部顺序完全打乱,就是为了生成下面交叉验证集。为了验证是否数据打乱,打出其前十行,发现顺序的确被打乱了 (由第一列粗体行数可知):