
Python部落(python.freelycode.com)组织翻译,禁止转载,欢迎转发。
在Recurse Center期间,我通读了《计算机程序的构造和解释》。这是一本出版于1985年的MIT的编程入门教材,用LISP的一种方言Scheme语言来教授编程。Scheme是函数式语言,我也一直喜欢学习新的函数式编程概念。
本文目的是向没有函数式语言经验或概念的程序员解释“尾递归”。
在解释尾递归之前,我们先看看命令式语言Python中的递归。
递归的一个问题

上面这段代码定义了一个返回数字n的阶乘的函数:factorial(n) = n * n - 1 * ... * 2 * 1。如果n = 4, 可以获得期望的结果是4 * 3 * 2 * 1 = 24。
当我们运行一个递归函数时,在运行背后到底发生了什么?任一函数被调用,就会往进程堆栈中加入一个包含与该函数有关的数据的栈帧,通过Python中的inspect模块,我们可以观察到发生了什么:

运行这个脚本得到:

我们可以看到,当inspect.stack()第一次被调用时,一个栈帧加到了堆栈中。再次调用,堆栈中就有两个栈帧了。
栈帧消耗内存,而一个Python进程只能分配到有限的内存。如果堆栈包含太多的栈帧,进程会耗尽所分配的内存,或者堆栈可能扩展到没有分配给该进程的内存空间而导致堆栈溢出。为了防止出现这样的问题,解释器会设置一个最大递归数的限制,可以通过调用sys.getrecursionlimit()来查看这个限制。在我的计算机上,这个限制是1000(注)。
每一次调用factorial(),一个新的栈帧就会加到堆栈中。如果加入了太多的栈帧,就会超过这个最大递归数的限制,解释器就会抛出如下异常:

由于栈帧产生系统开销,所以在命令式语言中,递归是内存密集型的操作。相比下面的使用迭代方式获取阶乘的函数:
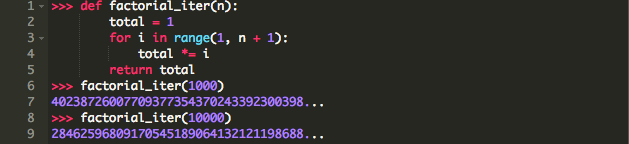
这个函数只产生了一个栈帧,比递归方式能更轻易处理大于n十倍或者更大的数值。
迭代递归
思考当解释器执行factorial(4)时发生了什么:

我们能看到创建了一系列延迟的操作,直到遇到n = 1时才会计算出最终结果。这是因为解释器为了后面的执行必须要记住并跟踪前面的操作。
如果我们重新定义factorial函数为:

并重新思考解释器做了什么:

我们看到一系列扁平的factorial()调用,状态保存在变量total中,而不是由解释器来保存。
尾递归
在“尾递归”语言中,以factorial_new这种方式定义的递归过程可以被解释器解释为迭代,从而不会带来递归的缺点。用这种优雅的递归过程,能使你获得和迭代一样的性能优势。解释器知道不需要在堆栈上创建更多的栈帧,从而抛弃创建栈帧的方式。
不幸的是,Python不是“尾递归”语言,所以factorial_new(1000, 1)仍然会抛出RuntimeError: maximum recursion depth exceeded。
更多信息,推荐参考《计算机程序的构造和解释》中的1.2.1小节。
注:在Python中可以调用sys.setrecursionlimit()来设置最大递归数,但通常不建议这么做。递归调用太多的函数应该使用迭代的方式来重写。
英文原文:https://jamesroutley.co.uk/tech/2017/06/04/tail-recursion.html
译者:scala



