上一次《维度：数学漫步》（上篇）的微剧场中，我们帮大家初步展示了四维空间，原本设想是不需要做下一篇了（大家不会对这么生僻的东西感兴趣吧），但实际上完全出乎意料。很多朋友留言要求下一篇。
这就有点难度了。
因为，木鱼当初看纪录片的时候，后半部分，也没有看懂……
只有硬着头皮上了，自己挖的坑，总得自己填上吧。
hopf 纤维丛
实际上，《维度：数学漫步》这个纪录片的后半部分说的有些跳跃，所以单看原片是比较难以理解的。
为了把这部分内容弄清楚，我们找到了官网文字版的详细推导过程，然后和纪录片对照着看，才真正弄明白，这比平时多花费了一个通宵。
之后再思考如何把这个难懂的想法表达出来，对原片进行剪辑、做画中画、加文字标示的补充，又再比平时多花了一个通宵，外加两个白天。
经历过这些，视频最后做出来，是相当，相当兴奋的。
考虑到爱学习爱成长的大家，看这期视频也要
消耗不少脑细胞
。
所以为大家准备了三个颈枕，看累了你就趴着睡一会（是不是很贴心）。
本文留言点赞的前3名，即可获得木鱼送出的颈枕1个，活动截止到3月14日晚上10点截屏。
颈枕 · 爱心款
下面就开始我们愉快的学习之旅吧。
先温故：
四维，正八胞体
看过上一期视频后，我们已经知道了：
四维空间里有一种叫三维球面的，被称为 S3
。
三维球面S3 其实是 四维超球体 的"表面"
，但它和我们经常见到的 二维球面 S2（球体的表面）不同。它不是二维的，而是三维的，正因为如此，它被称为 S3，
三维球面是具有“体积”的。
现在，我们就来深入讨论一下，什么是三维球面 S3？
▲
节目完整视频
前面我们说过，《维度：数学漫步》原片的后面部分，尤其是hopf纤维丛的部分，讲得有些跳跃，不是特别容易理解。
而后面二维球面S2上的一点，对应到三维球面S3上面的一个圆周，这种对应关系的图示也是讲得很快，容易让观众疑惑。
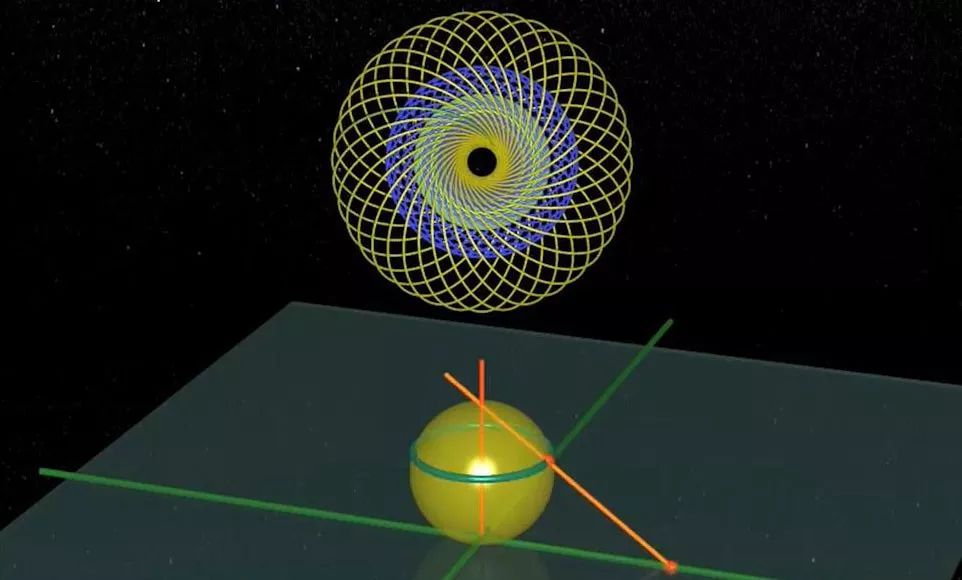
S2 球面纬线上的点所对应 S3 球面圆周所组成的“纬环面”在三维空间中的球极投影
我们是
通过看官方网站上文字版的详细推导过程，然后对照着纪录片，才把这部分弄明白。
官方网站文字版推导内容
微剧场叙述的时候，
我们将原本的逻辑进行了调整
，并和上部分的微剧场一样，加入了许多的画中画来方便大家理解。
也是希望大家尽量可以看懂
。
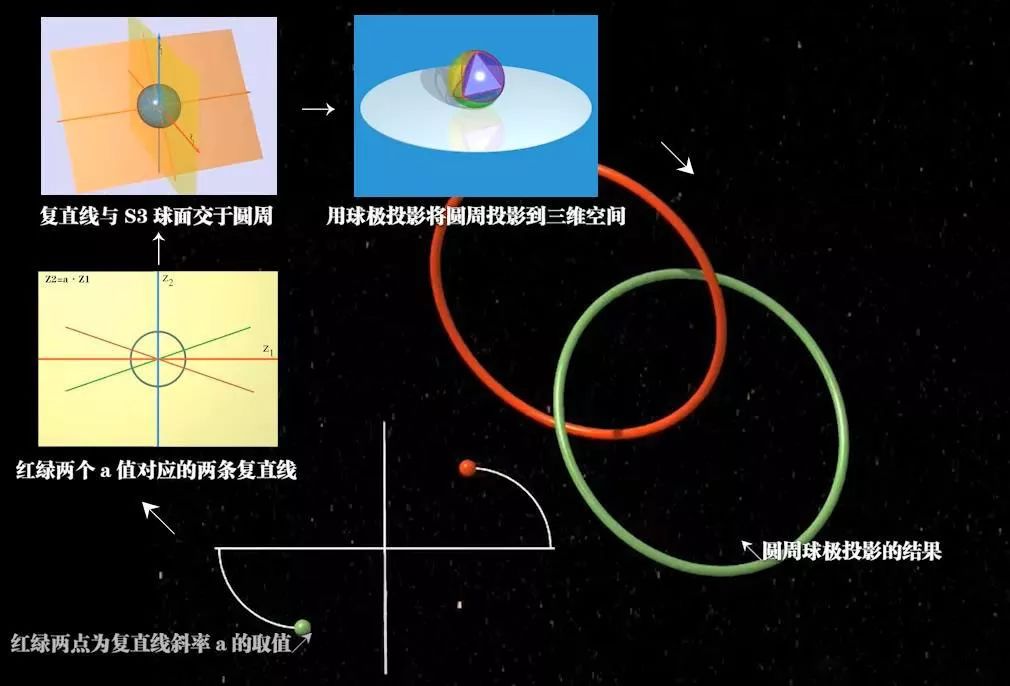
通过画中画，对比理解
调整过后的逻辑顺序
其实这一部分分形之前都是很好懂的，但
后面
复二维平面
直到
纤维丛
那里，是需要很仔细的看
，毕竟，一个从三维球面上的圆周到二维球面上的点的映射，真的不是那么容易想象。
这里需要提一下的是，纤维丛部分也是需要前面球极投影的知识作为基础的，所以
如果您是第一次看到这个系列，您可以去看微剧场的前半部分，传送门已经在文末准备好了。
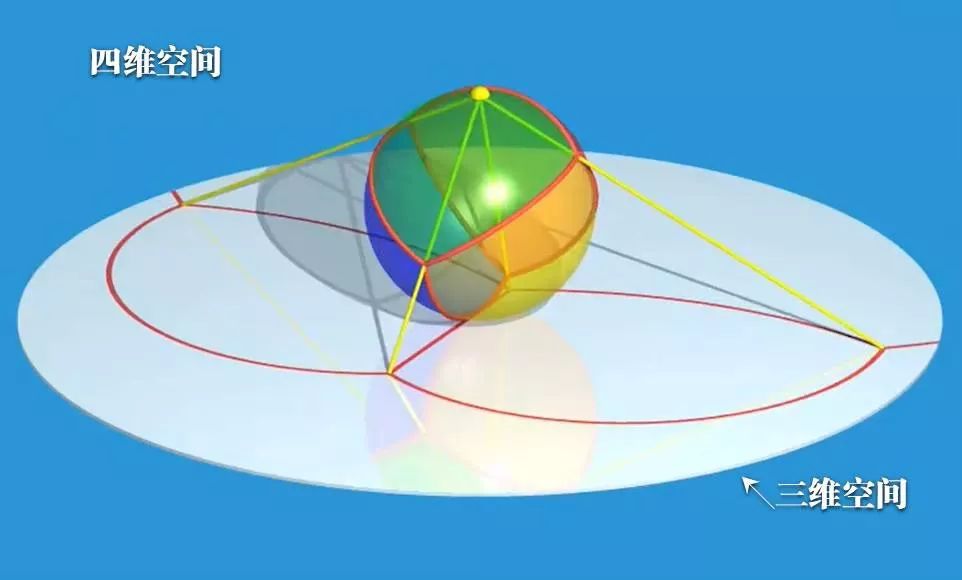
球极投影
最后，我们来聊聊数学和科学的区别。
数学作为一门工具，是科学的基础，
但是数学并不需要做实验来验证
，而实验才是自然科学的关键所在。
数学是关于抽象概念及这些抽象概念之间的关系的学问
，我的感觉是它更接近于哲学。
（实际上观点很多，有说数学是形式科学的，还有说数学是一种语言的，不过我的观点是数学接近哲学。仅个人观点。。）
所以，我们依靠数学工具所构建的四维空间，其实是
并不依赖于
“
实际上宇宙中到底有没有四维空间
”
这一命题的真伪的。
答案很简单，因为数学所研究的是抽象的概念。
S3 球面的“纬环面”和它的四个圆周族
不过，也正是因为数学超越现实的特点，所以有时会出现
人们研究一个新的物理现象却无法解释时，会突然发现，一个很早以前数学家凭空想出来的体系刚好可以对应。
毕竟，想象的空间是无穷的，数学上有些东西，乍一看没有用处，但实际上，可能是它发挥作用的时候，还没有到来罢了。
而
这其中所呈现的数学之美，实在是可以让人对未知心存敬畏。
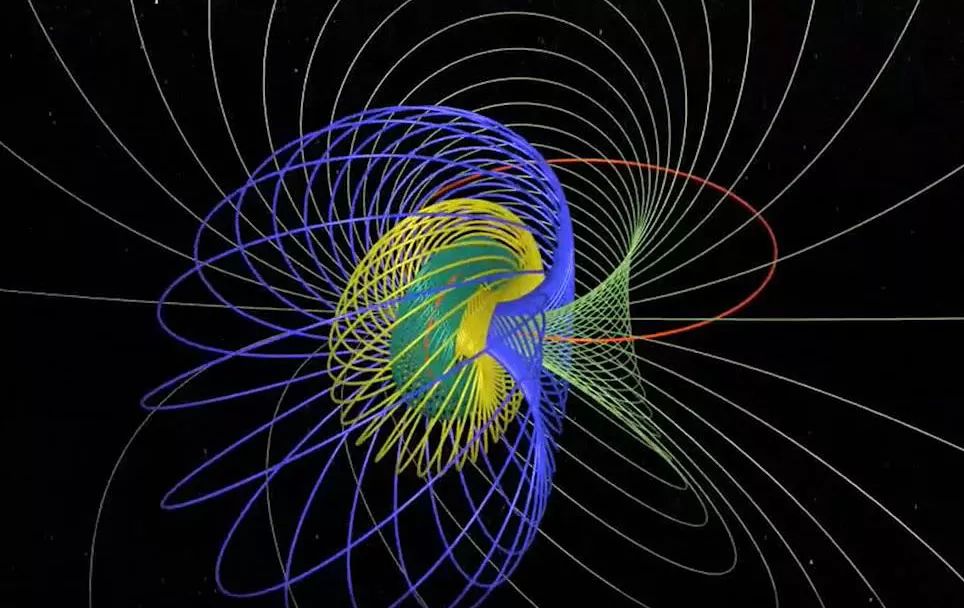
S3 球面纤维化以后在四维空间中旋转时，在常三维空间中的球极投影
