
picture from Internet
解析文章首发于唧唧堂网站www.jijitang.com
解析作者 | 唧唧堂经济学研究小组:
维垣
;审校编辑 |
悠悠 糖糖
论文基本信息:
本文是针对论文《有限重复囚徒困境中的理性合作(Rational Cooperation in Finitely Repeated Prisoner’s Dilemma)》的一篇解析。该论文于1982年发表于Journal of Economic Theory (JET),与同时期的几篇其他论文一道,开启了声誉(reputation)这一全新的的领域。从此,信息经济学的解释力大大增强。本文作者是素有“Gang of Four”之称的David Kreps,Paul Milgrom,John Roberts,和Robert Wilson。这是他们划时代的一次合作,也是[Kreps and Wilson, 1982]和[Milgrom and Roberts, 1982]等文献的集大成。该论文仅有7页之短,却被引高达3312次。
研究背景与问题
已有的文献指出,只有在无穷重复囚徒困境中才能出现理性合作;有限重复囚徒困境中仅存在一个子博弈完美均衡——每一回合都变节。后者是由倒推法给出的。然而本文通过引入
单边不确定性与策略限制
,成功建立了一个
合作均衡
;通过引入双边不确定性并放开策略限制,也成功建立了一个合作均衡。
模型
本文的模型是围绕阶段博弈为囚徒困境的标准重复博弈情形展开。本文中所有重复博弈中的阶段博弈都由下表所描述:

Fink即表示变节,而Cooperate代表合作。博弈由两个玩家参与——行玩家(ROW)和列玩家(COL)。令a > 1,b < 0,且a + b < 2。在重复博弈中,每一回合之间连个玩家均会被告知完美的历史信息集(perfect recall),包括之前他自己做了什么和对方做了什么。
重复博弈的报酬是每一回合未折现报酬之和
。
基准情形:
完整信息
在完整信息的情况下,这个模型有唯一的纳什均衡路径。在此路径上双方玩家都会总是选择变节。这个思路和Selten (1978)的连锁店博弈类似,都是使用倒推归纳法。然而,这个均衡路径明显是不符合现实情况(因为现实中确实能观察到合作)且极其低效的。实验中可以观察到此类有限次博弈往往以某些合作的行动开始,从而使他们得到的总收益严格优于均衡策略(Axelrod, 1981)。为了解释这一现象,本文引入了特定情况下的不完全信息。实际上,本文的作者发现这些不完全信息一定会将均衡路径引向一定的合作。一方或双方的不完全信息均可以被视为是玩家之间缺乏共识。事实上,这种情形非常常见,可以广泛用于多种经济、政治、军事问题中。
情形一:
一方对另一方是否理性的不完全信息
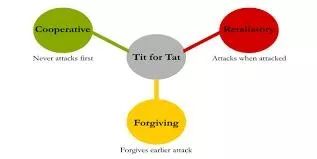
假设在博弈开始之前,列玩家不确定行玩家是否会“理性地”进行决策。特别地,列玩家认为行玩家是“理性人”之概率为1-δ,是“以牙还牙型玩家”的概率为δ(δ较小)。也就是说,有δ的概率行玩家只能采用以牙还牙策略(即第一回合从合作开始,之后每一回合都模仿对方玩家上一回合的策略)。实际上,本文选取以牙还牙的原因不只是因为它是最简单、最自然的策略,还因为它是Axelrod的囚徒困境锦标赛的优胜策略。
本文通过以下步骤证明下述序列均衡的策略组合成立:以双方合作开始,以双方变节结束,且变节次数不会超过一个上限。需要明确的是,此处回合按降序编号,即第一回合为回合n,第二回合为回合n-1… 最后一回合为回合1。这一编号方法采用了[Kreps and Wilson, 1982]的方法。
1.
在每一个序列均衡中,如果行玩家理性变成了共识,那么双方玩家在以后的回合中都会一直变节,从而他们之后的收益一直是0。
理由:显而易见。
2.
在每一个序列均衡中,如果列玩家在回合n+1变节,行玩家一定在回合n变节。
理由:若行玩家在回合n合作,行玩家理性就变成了共识。根据步骤1,双方之后都会一直变节,预期总收益为0;相反地,若行玩家在回合n变节,列玩家对行玩家是否理性的信念不会发生改变,从而使得未来出现合作策略这一事件有正的测度。因此行玩家在回合n变节是一个弱优势行为。
3.
对每一个序列均衡中的每一点而言,令列玩家对“行玩家以牙还牙”这一事件的期间信念(interim belief)为q(q不为0或1),令该点处剩余回合数为n(n较大)。
a)
如果列玩家在上一回合合作了,那么列玩家在剩下博弈中的预期收益至少是qn+b。
理由:列玩家上一回合合作了,假设行玩家是理性的(概率1-q),行玩家会变节,给以列玩家b的报酬,加上以后每回合0的报酬(双方皆变节);假设行玩家是以牙还牙的(概率q),行玩家会合作,并且双方会一直合作,给以双方每回合1的报酬,总共n回合。所以列玩家的预期收益为qn+(1-q)b > qn+b。
b)
如果列玩家在上一回合变节了,那么列玩家在剩下博弈中的预期收益至少是q(n-1)+2b。
理由:列玩家上一回合变节了,不管怎么样行玩家都会变节(根据步骤2)。所以如果列玩家在这回合和下回合都合作,她能得到至少q(n-1)+2b的收益。
c)
一个理性的行玩家在剩下博弈中的预期收益至少是q(n-1)+3b-a。
理由:理性的行玩家可以(继续)使用以牙还牙策略,从而使之后的收益至少都能达到列玩家收益最小值+b-a(考虑列玩家在之后某一时期变节),即q(n-1)+3b-a。
d)
如果还剩多于(2a-4b+2q)/q回合(而非任意的n回合),那么行玩家在该回合中采取以牙还牙策略的概率为1。因此在均衡路径上,如果剩余回合数大于或等于(2a-4b+2δ)/δ,列玩家的信念不会发生改变(q=δ)。
理由:若行玩家先变节,那么“行玩家理性”会变成共识,从而行玩家的最大收益是a;若行玩家不变节,她至少能得到b,且根据3(c),她之后的收益至少是q(n-1)+3b-a。所以当n大于(2a-4b+2q)/q时,合作是严格优势的。证明了前半句陈述,后半句陈述就显而易见了。
4.
在每一个序列均衡中,有任意一方出现变节的回合数有上界且存在上界小于总回合数的情况;在任意弱帕累托优势的序列均衡中,(2a-4b+2δ)/δ+1回合之前不会有变节出现。
理由:此为3(d)的推论。
至此,本文证明了合作确实存在于情形一的每一个序列均衡中。不完全信息的引入确实支撑了存在合作的序列均衡。除此之外,Milgrom and Roberts (1982)认为缺乏共识也起了作用。他们尝试用知识论的角度解释此问题。假设整个历史信息集分为三段:{1, 2, 3}。行玩家在1段是一个以牙还牙的玩家,在2、3段是理性的。行玩家知道他自己是哪种玩家,也就是说他的信息划分是{1}, {2, 3}。另一方面,列玩家的信息划分是{1, 2}, {3},也就是说直到3段他才能直接观察行玩家的类型。
假设历史信息集已经进入了3段,并且列玩家已经发现了行玩家是理性的,然而此时行玩家并不知道列玩家已经发现了自己。由于缺乏“理性”的共识,行玩家仍然会试图用合作去“欺骗”列玩家,而列玩家则“将计就计”,装作“被骗”,从而获得合作的收益。这种逻辑推导出的结果与情形一中分步骤推导的结果可以相互印证。值得一提的是,这种逻辑使得双方玩家更加理性,并且构建了一种策略性“将计就计”的行为。为了给出完全理性的情形,作者们又构建了情形二。

picture from internet
情形二:理性双方对于阶段收益的不完全信息
在此情形中,
双方的理性是共识
。然而,双方对互相阶段收益的信息是不完全的。假设双方玩家都认为对方会有一个小概率是“享受”合作的,也就是在矩阵中a<1。我们在这种情况下可以建立一个序列均衡,同样是以合作开始,以变节结束。然而,如果这是一个连续的博弈,正如Kreps and Wilson (1982)所描述的那样,那么存在一个自始至终都合作的均衡(运用价值函数和贝尔曼方程)。此处略去证明过程,具体可以参考几篇相关的文献,比如Kreps and Wilson (1982),Milgrom and Roberts (1982)。
然而,有两个限制需要澄清。第一,双边的不确定性是必要的。如果只要有一边对另一边的类型是确定的,那么结果就会导致全程皆变节。第二,在这种情形下合作式的均衡无法自然地发生(与情形一不同)。即使是双方确定对方“享受”合作也还不够,必须再加上他们对于双方将会合作已经有了共识。所以在这种情况下合作式的均衡可能并不能在这种情形下占主导地位,即使它是一个最有效的均衡。
参考文献:
Kreps David, Paul Milgrom, John Roberts and Robert Wilson (1982): “Rational Cooperation in Finitely Repeated Prisoner’s Dilemma,” Journal of Economic Theory, 27, 245-252.
Kreps David and Robert Wilson (1982): “Reputation and Imperfect Information,” Journal of Economic Theory, 27, 253-279.
Milgrom and Roberts (1982): “Predation, Reputation, and Entry Deterrence,” Journal of Economic Theory, 27, 280-312.
解析作者:维垣















