k临近法
(k-Nearest Neighbor, kNN)
是最简单的机器学习算法之一,但它仍然被广泛应用在
面部识别
,
电影/音乐推荐
,
检测疾病
等方面.如果一个概念很难定义,但是当你看到它的时候知道它是什么,那么kNN算法就可能是合适的方法.
kNN算法源于这样一个事实:
它使用关于一个案例的
k
个近邻的信息来
分类无标记
的例子,字母
k是一个可变选项,表示任意数目的近邻
.在选定
k
之后,kNN算法需要一个已经分好类的
训练数据集
,然后对没有分类(没有标记)的记录进行
分类
,kNN确定训练数据集中与该记录
相似度”最近”的k条记录
,将无标记的测试例子分配到k个近邻中
占比最大
的那个类中.
下面通过一个例子来形象表示kNN近邻分类算法的原理(来源网络博客):
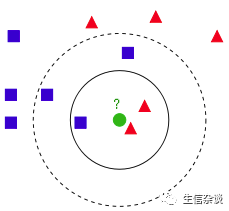
从上图中我们可以看到,图中的数据集都有了自己的标签,一类是
蓝色的正方形
,一类是
红色的三角形
,那个
绿色的圆形
是我们待分类的数据。
如果
K=3
,那么
离绿色点最近的有2个红色三角形和1个蓝色的正方形
,这
3个点投票
,于是绿色的这个待分类点属于
红色的三角形
.
如果
K=5
,那么
离绿色点最近的有2个红色三角形和3个蓝色的正方形
,这
5个点投票
,于是绿色的这个待分类点属于
蓝色的正方形
.
我们可以看到,KNN本质是基于一种数据
统计
的方法!其实很多机器学习算法也是基于数据统计的。
KNN是一种
基于记忆的学习
(memory-based learning)
,也是
基于实例的学习
(instance-based learning)
,属于
惰性学习
(lazy learning)
。即它没有明显的前期训练过程,而是程序开始运行时,把数据集加载到内存后,
不需要进行训练
,就可以开始分类了。
衡量近似度的方法:
最常用的是采用
欧式距离
(Euclidean distance)
,欧式距离是通过
直线距离
(as the crow flies)
来度量,即最短的直线路线.另一种常见的距离度量是
曼哈顿距离
(anhattan distance)
,即
两点在南北方向上的距离加上在东西方向上的距离
.
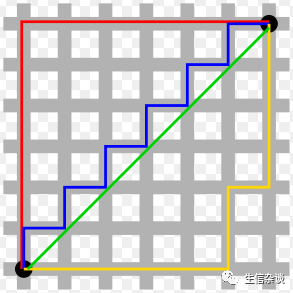
下图中
红线
代表
曼哈顿距离
,
绿色`
代表
欧氏距离
,
蓝色和黄色
代表
等价的曼哈顿距离
.
对于
名义特征
,如
性别
,
类别
或其他属性需要将其转换为
数值型
格式。一种典型的解决方法就是利用
哑变量编码
(dummy coding)
,其中
1
表示一个类别,
0
表示其他类别,例如,可以构建性别变量的哑变量编码:

创建哑变量的方法可以被更广泛的应用,一个具有
n
个类别的名义特征可以通过对特征的
(n-1)
个水平创建二元指示变量。例如,为一个具有3个类别的
温度变量
(hot、medium和cold)
进行哑变量编码,可以用
(3-1=2)
个特征进行设置,如下所示:

只需知道
hot
和
medium
的值同时为
0
就足以说明温度是
cold
,因此我们再设置
cold
变量。哑变量编码的一个方便之处就在于哑变量编码的特征之间的距离总是
1
或
0
,与
min-max标准化
时的数值数据一样,这些值落在了一个相同的范围内,不需要进行额外的变化。
如果名义变量是有序的,那么一种哑变量编码的代替方法就是
给类别编号并且应用min-max标准化
。例如,
cold
,
warm
和
hot
可以编号为
1
、
2
和
3
,
min-max标准化
后为
0
、
0.5
和
1
。
不过需要注意的是,只有当类别之间的步长相等时,才能应用该方法
。例如对于收入分类,
poor
、
meddle
和
wealthy
是有序的,但三者之间的差异可能是不同的,由于组别之间的差异不相等,所以使用哑变量编码是一种更保险的方法。
如何选择一个合适的k:
数据的
过度拟合
和
低度拟合
之间的平衡问题称为
偏差-方差权衡
(bias-variance tradeoff)
.选择一个
大的k
会
减少噪声数据对于模型的影响
,但它会似分类器产生
偏差
.
过度拟合:
例如我们假设一个极端的情况,即设置一个非常大的
k
,它等于训练数据中所有的观测值的数量.由于每一个训练案例都会在最后的投票中进行表决.所以被测试的案例将会被分类到数量最多的那一个类里.因此,模型总会预测结果为
数量最多的那个类
,而不管哪个邻居是最近的.
低度拟合:
假设
k
为1.即只使用最近的一个邻居投票决定未知标签案例的分类.如果这个标签有误,则无论其他临近最近的有多少个标签都没用,因为只有最近的那一个投票有效.所以这样将预测得到一个错误的结果.
显然,最好的k值应该是这两个极端值之间的某个值.
在实际中,
k值
的选取决定于要学习的概念的难度和训练数据中记录的数量.一种常见的方法是
从k等于训练集中案例数量的平方根开始.
比如训练集中有100个案例,则k可以从10开始进行进行进一步筛选.
然而这样的规则并不总能产生一个最好的
k值
.另一种方法是基于各种测试数据测试多个
k值
,并选择一个可以提供最好分类性能的
k值
.并且,除非数据的噪声非常大,否则大的训练集可以使
k值
的选择不那么重要.
还有种方法是选择一个较大的
k值
,同时用一个
权重投票
(weighted voting)
,在这个过程中,认为较近邻的投票比远的投票更有权威.许多kNN程序都提供了这样的选项.
特征范围标准化:
在应用
kNN
算法之前通常需要将特征数据转换为
一个标准的范围内
,这个步骤的合理性高度依赖于特征是如何被度量的.如果某个特征具有比其他特征更大范围的值,那么距离的度量就会强烈地被这个具有较大范围的特征所支配.
标准化化的方法便是搜索或者放大特征的范围来重新调整特征,使得每个特征对距离公式的贡献相对平均.传统的归一化方法是
min-max标准化
(min-max normalizatio)
.该过程变换特征,使被变换数据的所有值都落在
0~1
的范围内,公式如下:
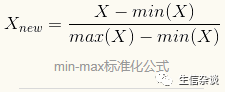
min-max标准化
的特征值可以这样解释:按
0%~100%
来说,在原始最小值和原始最大值的范围内,原始值到原始最小值的距离有多远.
另一种常见的变换称为
z-分数标准化
(z-score standardzation)
.公式如下,含义是原始值减去特征X的均值后,再除以X的标准差.
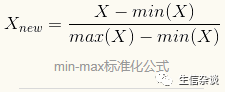
这个公式的性质是根据正太分布的性质(即每一个特诊的值落在均值上下的标准差的数量)来调整每个特征的值,所得到的值称为
z-分数
(z-score)
.z分数落在一个无界的负数和正数构成的范围内,与
min-max标准化
后的值不同,没有预定义的最小值和最大值.
用于
kNN
训练集的标准化方法也应该用于要待分类的测试集样本.但是对于
min-max标准化
,这可能就导致一种棘手的情形,即
测试集
的最小值或最大值可能在
训练集
的范围之外.比如
测试集
的一个特征的值为
1,3,5,7,9
。经
min-max标准化
后为
0,0.25,0.5, 0.75,1.00
;但
训练集
中如果这个特征值存在
0,10
等处于测试集范围之外的数值,如果也使用
min-max标准化
则导致预测结果偏离不准确。
所以,在测试集范围大于训练集范围的情况下,使用z分数标准化是种更好的方法。但前提是两者具有相同的均值和标准差。
例子——使用kNN算法诊断乳腺癌:
数据来源是
UCI机器学习数据仓库
的
威廉康星乳腺癌诊断数据集
。该数据可以从 http://archive.ics.uci.edu/ml 获得,但下载下来的还得整理列名,我已经下载并整理好,大家可以从这里下载现成的数据 : http://pan.baidu.com/s/1qY4WEfE .
这个数据集包含
569
例细胞活检案例,每个案例有
32
个乳房肿块活检图像显示的细胞核的特征。第一个特征是
ID
,第二个是这个案例的
癌症诊断结果
,癌症诊断结果用编码
“M”
表示恶性,
B
表示良性。其他
30
个特征是数值型的其他指标,包括细胞核的
半径
(Radius)
、
质地
(Texture)
、
周长
(Perimeter)
、
面积
(Area)
和
光滑度
(Smoothness)
等的`均值、标准差和最大值。部分数据如下:



















