
德国数学家波恩哈德·黎曼于 1859 年提出:黎曼 ζ(s) 函数的非平凡零点都在复平面上的一条实部为 0.5 的直线上。
近日数学家发现,黎曼 ζ(s) 函数的解和另外一个方程的解有关系,
而后者很有可能是证明黎曼猜想的一条捷径。
如果这个结果能被严格证明,作为数学界最大猜想之一的黎曼假设将获得最终证明,证明者即能摘得克雷数学研究所的1百万美元悬赏。
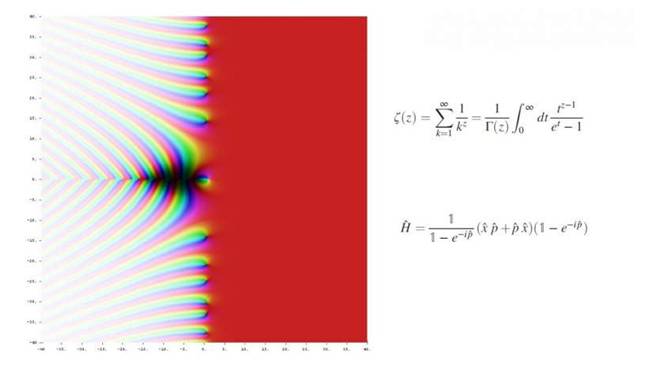
黎曼猜想自 1859 年提出之后的 100 多年里,数学家试图走出证明的关键一步:
找到一种算子函数
。
今天,这一梦寐以求的函数可能终于出现了。
多杰·布罗迪(Dorje Brody)是伦敦布鲁内尔大学数学物理学家,也是相关论文的共同作者。他表示:这是首次发现如此简洁的算子,其特征值(eigenvalue)与黎曼 ζ(s) 函数的非平凡零点精确相关。
接下来,数学家要证明下一步:
所有特征值都是实数
。
如果确实能证明这一点,黎曼猜想将最终获得证明。布罗迪和其他两位共同作者——来自华盛顿大学圣路易斯分校数学物理学家卡尔·本德(Carl Bender)和来自西安大略大学的马库斯·穆勒(Markus Müller)——在《Physical Review Letters》上发表了相关论文。
素数空间
黎曼猜想对数论,特别是素数理论有重要意义
。1859年,德国数学家伯恩哈德·黎曼(Bernhard Riemann)研究了素数的分布问题——给定整数N,有多少个小于N的素数?
黎曼推测,所有小于N的素数的分布,跟黎曼 ζ(s) 函数的非平凡零点相关。(所谓的零点,即为使方程等于零的解(s值)。而当是负偶数时,方程则一定为零,因此这些零点被看作是 ζ(s) 函数的平凡零点,并不重要。)
黎曼假设认为:所有非平凡零点都落在复平面上的一条实部等于0.5的直线上,即实部总是等于0.5,而虚部不同。
150年来,数学家发现了不计其数的非平凡零点,所有的点的实部也确实是0.5,跟黎曼的猜想相符。因此,数学家普遍认为黎曼猜想是正确的,并已经基于该猜想做了很多工作。但是,
黎曼猜想本身,至今未被证明
。
等效解
函数理论提供了证明黎曼猜想的有力工具。它指出:所有非平凡零点构成一个离散实数的集合。有趣的是,某物理学上有广泛应用的函数——微分算子——其特征值跟非平凡零点的集合很相似。
20 世纪 90 年代初,这种相似性让一些数学家思考:可能存在某种微分算子,其特征值就是黎曼 ζ(s) 函数的非平凡零点。
今天,这个猜想被称为希尔伯特-波利亚猜想,尽管大卫·希尔伯特(David Hilbert)和乔治·波利亚(George Pólya)都没有在这方面发表任何著作。希尔伯特-波利亚猜想包括 2 步:1)找到 1 个算子,证明其特征值就是黎曼 ζ(s) 函数的非平凡零点;2)证明这些特征值都是实数。
目前,相关的研究工作主要集中在第 1 步。数学家已经确认了一种算子,其特征值精确对应于黎曼 ζ(s) 函数的非平凡零点。第 2 步工作刚刚开始,数学家甚至还不能确定,证明第 2 步到底有多难。他们能确定的是,还需要更多的工作。
算子
有趣的是,这种起关键作用的算子跟量子物理有密切联系。1999年,数学物理学家米切尔·博里(Michael Berry)和约拿单·基廷(Jonathan Keating)研究希尔伯特-波利亚猜想时,他们提出了另外一个重要的猜想:
如果这种算子确实存在,那么它应该对应于一种具有某些特性的理论量子系统
。这个猜想被称为博里-基廷猜想,但是之前谁也没找到这个系统。
如今,布罗迪称,
他们确定了博里-基廷哈密尔顿算子的量子化条件,并基本证明了博里-基廷猜想
。
哈密尔顿算子通常用来描述一个物理系统的能量,但是博里-基廷哈密尔顿算子的奇异之处在于,至少目前,科学家认为,它并不对应于任何物理系统,而是一个纯数学函数。
布罗迪表示,他们的证明工作基于启发性分析方法,这种方法源于已经有大约15年左右历史的伪厄米PT-对称量子理论。因此,他们将文章发表在《Physical Review Letters》,而不是数学期刊。
希尔伯特-波利亚猜想认为,关键的哈密尔顿算子应该也是厄米算子,而量子理论中,也通常要求哈密尔顿算子同时也是厄米算子,因此希尔伯特-波利亚猜想和量子理论有天然的联系。布罗迪等人提出了希尔伯特-波利亚猜想的伪厄米形式,并将其作为下一步的研究重点。
真正的解
现在,最大的挑战是证明:
该算子的特征值都是实数
。
总体来说,科学家对克服这个挑战表示乐观。原因在于,他们有一样法宝可以利用,那就是 PT 对称性。PT 对称性是量子物理的概念——如果该系统满足 PT 对称性,当你改变四维时空的的符号时,变换后的结果和变换之前相同。
尽管真实的世界一般不满足 PT 对称性,物理学家构建的这种算子却具有这种特性。然而,科学家现在需要证明,这种算子虚部的 PT 对称性被打破。若能做到这一点,则该算子的特征值都是实数——最终证明黎曼猜想。
科学家普遍认为,黎曼猜想的证明对计算机科学,特别是密码学有重大意义。此外,数学家也希望知道论证的结果到底会对理解基础数学原理带来些什么影响。
布罗迪表示,尽管他们还不能预测研究结果对数论的具体影响,但有理由期待后继成果。
编译:离子心
https://phys.org/news/2017-04-insight-math-million-dollar-problem-riemann.html
MIT Technology Review 中国唯一版权合作方,任何机构及个人未经许可,不得擅自转载及翻译。
分享至朋友圈才是义举

一个魔性的科幻号,据说他们都关注了





