由于可转债条款的复杂性,能否为可转债实现理论上的精确定价成为市场长期以来关注的焦点问题。完善的可转债定价模型,能够为投资者的投资行为提供有力的参考,同时为可转债的上市价格提供有价值的论证。因此我们将在基础研究系列中专门开辟一个子系列探讨理论定价的来龙去脉,本专题将首先聚焦于定价模型的理论基础。
可转债定价发展史
可转债可以看作债券与期权的组合,由于期权定价在可转债定价中显得尤为重要,故可转债定价理论在1973年经典期权定价理论问世后慢慢发展起来,Ingersoll(1977)在这方面做出了开创性的研究。具体来看,
按定价思路划分,可转债定价可以分为整体定价法与成分定价法。按定价技术划分,可以分为解析解法、有限差分法、二叉树法、蒙特卡罗法。按风险因子划分,可以分为基于公司价值的定价、基于股票价格的定价。
成分定价与整体定价两类思路
在研究可转债定价问题时,我们需要首先明确是对可转债整体进行定价,还是将可转债分解为债底和期权两个部分分别进行定价。就理论而言前者称为整体定价法,后者称为成分定价法。
成分定价法将可转债价值拆解为债底价值与期权价值之和。
债底计算不存在难度,期权价值直接借助已有的期权定价理论计算,主要包括Black-Scholes公式、二叉树法、有限差分法、蒙特卡洛法等。
整体定价法的思想则是直接以可转债整体作为定价对象。
定价依然依托期权定价理论,但不对债底部分和期权部分进行区分,且需要进一步考虑债券的信用风险、利率条款等各方面影响因素。
成分定价法与整体定价法的连接点是Ingersoll(1977)的研究。Ingersoll采用的是整体定价法,但在特定假设下,得出了整体定价法与成分定价法结果相等的结论。
具体来看,Ingersoll结合Black-Scholes模型构造可转债价格的偏微分方程,并利用无套利原理得到偏微分方程的边界条件。模型假设为
可转债不支付现金股利、转债利息部分是贴现支付的,
因此得到偏微分方程的解析解,并据此证明在这种假设下可转债价格可以被分解为普通贴现债券价格与认股权证价格之和减去赎回期权价格。
但上述假设忽略了期权的美式特征,在现实中很难成立。
成分定价法把转股期权、赎回期权、回售期权看作是相互独立的,忽略了它们之间的相互作用。Ho和Pfeffer(1996)的研究表明,这种忽略容易造成较大的定价偏差。
基于上述原因,在转债定价的发展历史中,绝大部分研究采用的是整体定价法,成分定价法仅能视作一种粗略的简化。
在使用整体定价法时,由于很难得到解析解,故通常需要借助二叉树法、有限差分法、蒙特卡洛法等数值解法。
以下我们对二叉树法、有限差分法、蒙特卡洛法的介绍均是基于可转债整体的定价方法,而不是只针对期权部分进行定价。
综合上述分析,我们将两种定价思路的优缺点进行比较,具体如表1所示:

多种定价技术实用性有别
在讨论可转债定价技术之前,我们需要先对期权定价的历史进行回归。期权定价的方法主要包括Black-Scholes公式、二叉树法、有限差分法、蒙特卡洛法。其中Black-Scholes公式属于解析方法,由Black和Scholes在1973年提出。二叉树法、有限差分法、蒙特卡洛法属于数值解法,其中二叉树法由Cox、Ross、Rubinstein在1979年提出,有限差分法由Brennan和Schwartz在1977年引入期权定价,蒙特卡洛法由Boyle在1977年引入期权定价。
可转债定价技术是在期权定价技术的基础上发展起来的。Ingersoll(1977)由于模型假设的缘故得到了可转债的解析解,Brennan和Schwartz同年将有限差分法应用到可转债定价中,二叉树法的出现进一步扩充了可转债的定价技术。蒙特卡洛法则是在Longstaff和Schwartz(2001)较好的解决美式期权定价问题后才较为普遍的应用到可转债定价中。
解析解法
解析解法指通过解析表达式对可转债进行定价的方法。
如果不考虑赎回期权、回售期权,解析解法的公式通常为:
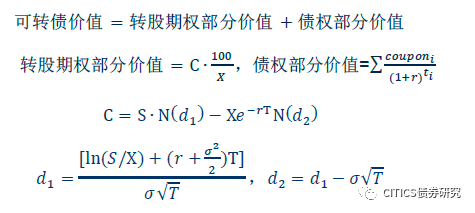
其中X表示转股价,S表示正股价,
表示正股年化波动率,
表示年化无风险利率。采用同样的方式,可以用Black-Scholes公式为赎回期权、回售期权定价。综合考虑赎回期权、回售期权后的解析解公式为:
可转债价值=普通债券价值+转股期权价值(看涨期权)-发行人赎回期权价值(看涨期权)十投资者回售期权价值(看跌期权)。
上述方法的优点是操作简单、运行效率极快,但同样存在较明显的缺陷。
一是属于成分定价的思路,忽略了期权之间的联系。二是解析解很难包含股利发放、提前执行、路径依赖等特征,使每项期权的估计不够精确。
为了规避上述缺点,另有学者从其他角度拆借可转债期权得到解析解。比如,周其源、吴冲锋、刘海龙(2009)不再用普通期权,而是用奇异期权对可转债价值进行拆借。具体的,可转债被分解为一种与之对应的普通贴现债券,两种立即支付型规则美式二值买权、一种规则上敲出买权和一种延迟支付型规则美式二值买权,并得到上述4种奇异期权的解析表达式。通过与蒙特卡罗法的结论对比,证实该方法有较高的定价效率。但该方法没有考虑回售条款,且难以考虑债息、锁定期、信用风险等情况。
有限差分法
在Ingersoll(1977)的研究中,由于模型假设过于简化,得到了偏微分方程的解析解。在之后的研究中,由于进一步考虑了定期付息、股票分红、回售等情形,导致偏微分方程不再有解析解,需要借助于数值解。故求解此类模型通常借助于有限差分法或二叉树法,而有限差分法在学术论文中则有更普遍的应用。
具体来看,假设股票价格服从如下的几何布朗运动:

在此基础上,进一步给出可转债价值P需要满足的边界条件。基于偏微分方程和边界条件即可利用有限差分法求解可转债价值。具体而言,
有限差分法的核心思想是对导数进行离散化,把上述偏微分方程转化为差分方程,然后通过迭代法进行求解。
根据对导数差分方式的不同,又分为显示差分法和隐式差分法。显示差分法工作量小,易于应用,但稳定性较差,可能不会收敛于偏微分方程的理论解;隐式差分法的收敛稳定性则更好。
由于可转债的偏微分方程与Black-Scholes偏微分方程相同,故在实际应用中区别主要在于对边界条件的处理。由于在数学和数值分析文献中有很多帮助改进有限差分法的算法,使其相对二叉树法运算速度能够更加迅速,运算结果更加精确。二叉树法的灵活性则差于有限差分法,因此在学术论文中有限差分法得到了更广泛的应用。
二叉树法
二叉树法也是求解偏微分方程的一种数值算法。该方法只需要利用边界条件,不需要使用偏微分方程,但可以证明当二叉树步数足够多时(一般为大于200步),二叉树模型的解会收敛于Black-Scholes偏微分方程的解。
从某种意义上看,有限差分法可以看作是二叉树法的推广和一般化,两者均是从后向前的定价思路,从而能更好的解决提前执行的美式期权问题,但相应的难以解决路径依赖期权的问题。
与有限差分法相比,二叉树法的优点在于更简单直观、容易实现,因此在金融实务中得到了更广泛的应用。在后文中,我们将对基于二叉树的可转债定价方法进行详细的介绍。
基于蒙特卡洛法的定价
蒙特卡洛法是期权定价的一种重要方法。虽然蒙特卡洛法可以很好的解决路径依赖的问题,但采用的是从前向后推进的方式,与美式衍生品从后向前推进的最优执行策略相矛盾,故在相当常一段时间内认为只适合解决类欧式期权的定价问题。而可转债的内嵌期权通常被认为是美式的,故早期应用蒙特卡洛方法进行可转债定价的研究较少。
Longstaff
和Schwartz(2001)发明的LSM模型很好的解决了美式期权的蒙特卡洛定价问题,该方法易于实施,得到了广泛推广。之后LSM模型也引入了可转债定价的研究中,代表性的研究有C Wide和A Kind(2005)等。但解决美式期权问题后,蒙特卡洛法依然存在运算速度较慢的问题,其效率与二叉树法和有限差分法存在较大差距。在后文中,我们将对基于蒙特卡洛法的可转债定价方法进行详细介绍。
下修条款的处理技术
上述定价技术均是基于国外的研究。相对于国外,国内可转债的一个重要不同是下修条款的重要性不可忽视。
在这方面具有代表性的研究是郑振龙、林海(2004)(以下简称ZL模型)。
我们在《转债基础研究系列之四:转股价下修与提前赎回条款对转债价格的冲击路径解析》中已经论证转发行公司只有在面临回售压力时才会调低转股价。假设下修后的转股价为Xt
,应满足:
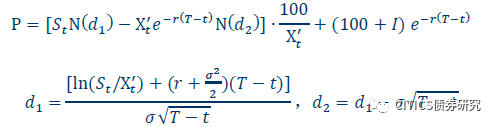
其中t为当前触发回售条款的时刻,T为到期时刻;I为从t到T时刻尚未支付的利息。
综合上述分析,我们将定价技术的优缺点进行比较,具体如表2所示:

定价依赖于风险因子的运动
在为可转债定价时,我们需要刻画可转债价格的运动,价格的运动依赖于基础风险因子的运动。可转债定价常用的风险因子包括两大类:公司价值和股票价格。
基于公司价值的定价
早期可转债定价的风险因子多为公司价值。
采用公司价值而不是股价描述可转债,主要是因为在理论上用公司价值可以更合理的刻画可转债的边界条件。
由于可以包含进公司破产等情形,从而更容易描述可转债的信用风险。但由于公司价值难以直接衡量,故该方法实用性较差,不是可转债定价的主流。
在基于公司价值的定价方法基础上,如果将利率作为一个风险因素而不是常数,就衍生出了基于公司价值的
双因素定价方法
。对利率的建模方式通常有Ho-Lee模型、CIR模型等。
基于股票价格的定价
McConnell
与Schwartz(1986)首先将股票作为风险因子衡量可转债的价值,
之后基于股票价格的定价取代基于公司价值的定价成为可转债定价的主流。
与基于公司价值的定价方法相比,
由于股价可以直接观测,故其实用性大大增强。
而与基于公司价值的定价方法相比,
基于股票价格的定价方法最大的问题是难以将信用风险考虑进可转债定价的边界条件。根据Kang和Lee(1996)、Hamilton(2001)的研究,在进行可转债定价时,信用风险是不可忽略的。
但因为股票价格不能为负,这就排除了未到期破产和到期违约的可能性。故在实际中为了考虑信用风险,通常做法是在无风险利率上加入信用利差作为贴现率。
为了消除简单使用放大的无风险利率作为贴现率衡量信用风险的不一致性,出现了很多相关的研究。
代表性的是Goldman Sachs(1994)。
Goldman采用二叉树对可转债进行定价。这一方法假设当下一个节点的股价远远高于转换价格的时候,期权处于深度实值状态,使用无风险利率进行贴现;当下一个节点的股价远远低于转换价格的时候,期权处于深度虚值状态,投资者相当于持有具有风险性的公司普通债券,所以贴现率要加入信用风险利差。
但该方法有一个参数是股票借出利率,在我国尚不普及,故模型使用存在一定的局限性。
另一个代表性的研究则是Tsiveriotis和Fernandes(1998)(以下简称TF98模型)。
该方法将可转债分为债权部分和股权部分,债权部分会遭遇违约风险;股权部分则由于发行者能一直发行或交易自己的股票,违约风险是0。通过区别对待,模型也部分解决了信用利差的内在不一致问题。TF98模型最初采用有限差分法求解,Hull(2000)则利用二叉树方法描述了TF98模型。
与基于公司价值的定价方法类似,基于股票价格的定价方法也通过将利率作为风险因素衍生出了双因素模型。进一步,由于基于股票价格的定价方法还使用了信用利差这一参数,如果假设这一参数不为常数,就衍生出了
三因素模型
,代表性的研究是Davis和Lischka(2002)。
综合上述分析,我们将不同风险因子的优缺点进行比较,具体如表3所示:

可转债定价方法详解
综合考虑可转债的定价方法。
在定价思路上我们建议使用整体定价法
,不使用成分定价法的原因是其不适合为不可分离转债定价。
在定价方法上我们建议使用二叉树方法及蒙特卡洛法。
不使用解析解法的原因是定价误差较大。不使用有限差分法的原因是该方法没有二叉树法直观,且其与二叉树法能解决的是同一类问题,优势主要在于速度更快、精度更高。但在实务中,我们通过实践发现二叉树法已经拥有了较高的运行速度和精度,故无需使用有限差分法即可实现合理定价。
在风险因子的选择上,我们建议使用基于股票价格的定价
,因为股票价格更容易获得,且该方法是目前的主流。
另一方面,
在蒙特卡洛法中我们建议采用郑振龙、林海(2004)的思想进行转股价下修。
由于转股价下修带有路径依赖特性,不适合二叉树法从后向前的定价方式,故
在二叉树法中只考虑回售条款而不考虑下修条款。
下面,我们将对二叉树法和蒙特卡洛法进行具体的介绍。在二叉树法中,我们将介绍不包含信用风险的二叉树模型、考虑信用风险的TF98模型;在蒙特卡洛法中,我们将介绍ZL模型、LSM模型。
符号说明
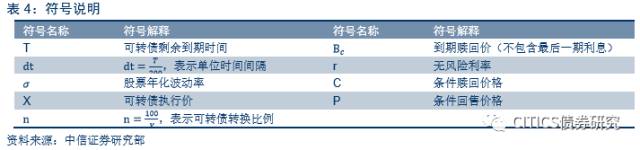
二叉树法
不包含信用风险的二叉树模型

考虑信用风险的TF98模型

蒙特卡洛法
ZL
模型
ZL
模型思想
ZL
模型由郑振龙、林海(2004)提出。模型提出了关于中国可转债市场的几条推论:
推论1:
中国可转债发行公司的最优决策是尽可能早地、以尽可能高的转股价格促使投资者将可转债转成公司股票。
推论2:
在中国特殊的制度背景下,可转债中股性占了绝大部分,而且中国的信用风险溢酬不高,因此将可转债的股性和债性统一起来,全部使用无风险利率进行贴现,并不会对可转债的价值造成很大的影响。
推论3:
因为中国可转债发行条款均规定转股价将根据公司股票的股利政策进行相应的调整,可转债中的转股权不会被提前执行,它实际上是一个欧式看涨期权。
推论4:
公司会选择尽可能短的赎回期。
推论5:
可转债发行公司只有在面临回售压力时才会调低转股价,调低幅度也仅以使得可转债价值稍微超过回售价格为限。
根据推论1-5,在可转债的生命周期内,
如果满足回售条件,发行人将修正转股价,使投资者不会回售;除了满足赎回条件使投资者提前转股以外,可转债将被持有至到期,可转债中的转股权被视为欧式期权。
故下修的转股价
就是使得t时刻回售价值等于继续持有转债价值的转股价,而t时刻继续持有转债的价值就是用B-S公式算出的欧式期权价值乘以转换比例,再加上纯债部分的价值。
ZL
模型实现步骤

LSM
模型
LSM
模型思想
根据Z-L模型的假设,由于可转债转股价会根据股利政策进行修正,在非赎回路径上可转债不会提前行权,期权可以作为欧式期权看待。但在现实中可转债会提前行权,应当被看作美式期权,故上述假设与实际有所不符。基于此,我们使用前文介绍的LSM模型对ZL模型进行修正。在思想上,LSM模型假设非赎回路径上的可转债可以在转换期内随时行权,其他处理方法与ZL模型相同。
具体来看,在蒙特卡洛每个时间节点上,投资者知道瞬间行权的价值,却不知道继续持有转债的价值。
LSM方法的思想在于将期权的持有价值Ft
看作当前状态变量St
的线性组合
:

其中常见的线性组合形式是Ft=a0+a1St+a2St平方
。具体到可转债,在t时刻瞬时履约价值大于0的样本中,以t+1时刻贴现的现金流作为因变量,以t时刻的转换价值作为自变量,进行最小二乘回归得到参数估计,代入t时刻的转换价值即可得到t时刻持有价值的最佳线性估计。
在得到持有价值后,通过比较持有价值与转换价值,即可得到投资者在每个时间点上的决策。基于此,即可得到转债的当前理论价值。
LSM
模型实现步骤






